Hoe asymmetrie in de statistiek te interpreteren: met voorbeelden

In de statistiek gebruiken we scheefheid om de symmetrie van een verdeling te beschrijven.

We zeggen dat een verdeling van gegevenswaarden scheef is als deze een ‘staart’ heeft aan de linkerkant van de verdeling:

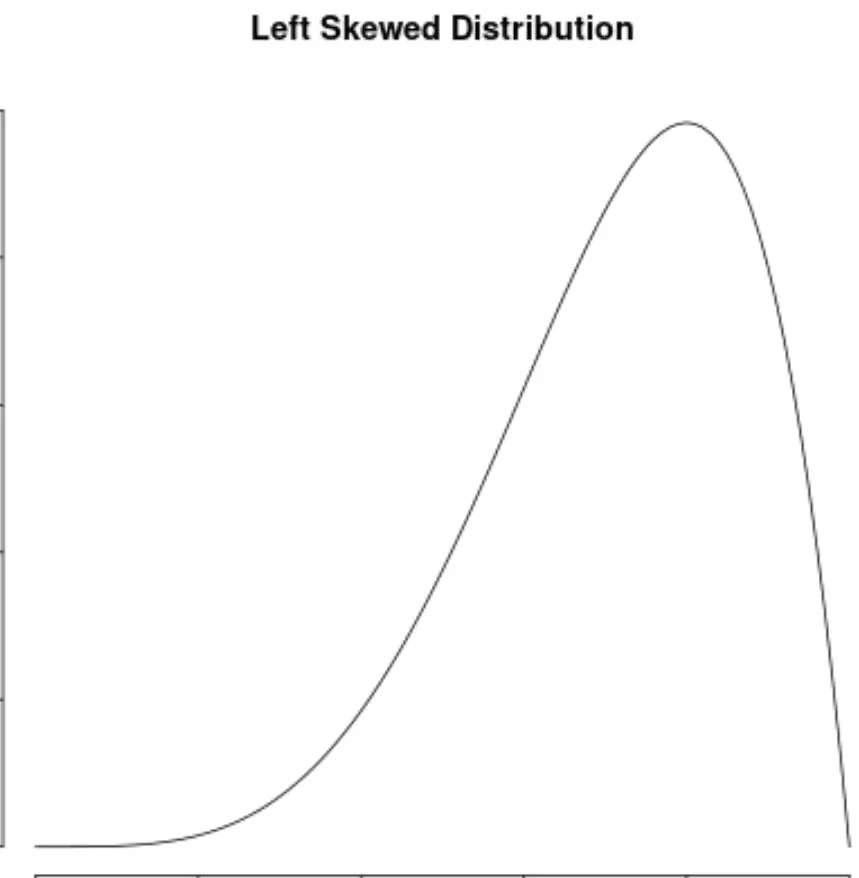
Er wordt gezegd dat een verdeling rechtsscheef is als deze een ‘staart’ heeft aan de rechterkant van de verdeling:

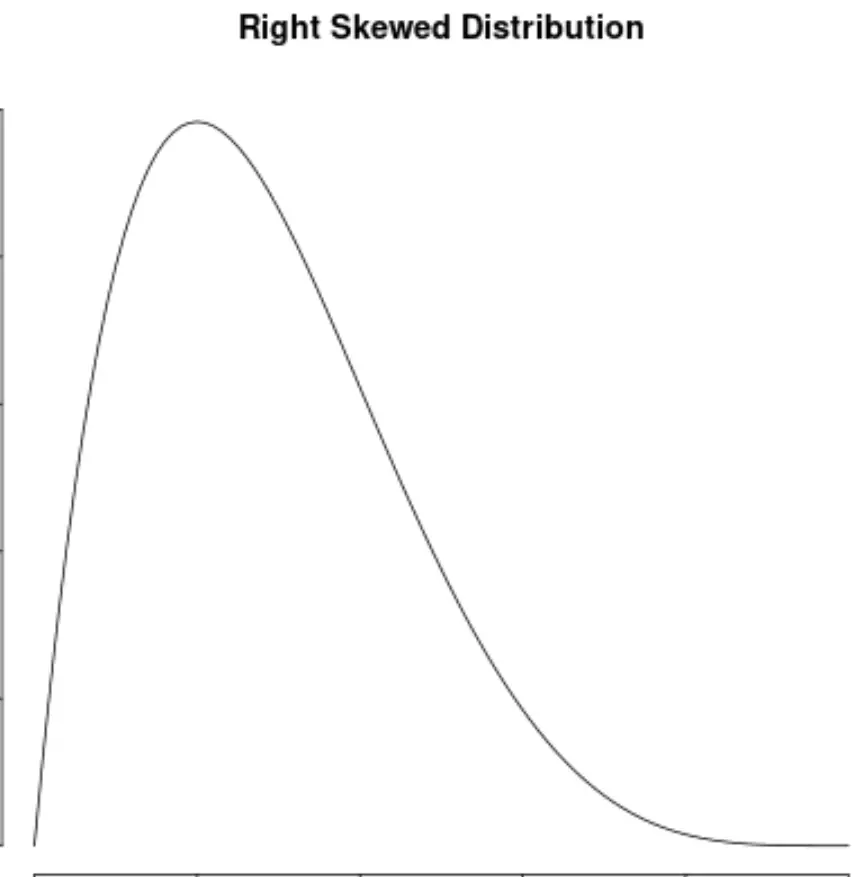
En we zeggen dat een verdeling geen asymmetrie heeft als deze aan beide kanten symmetrisch is:

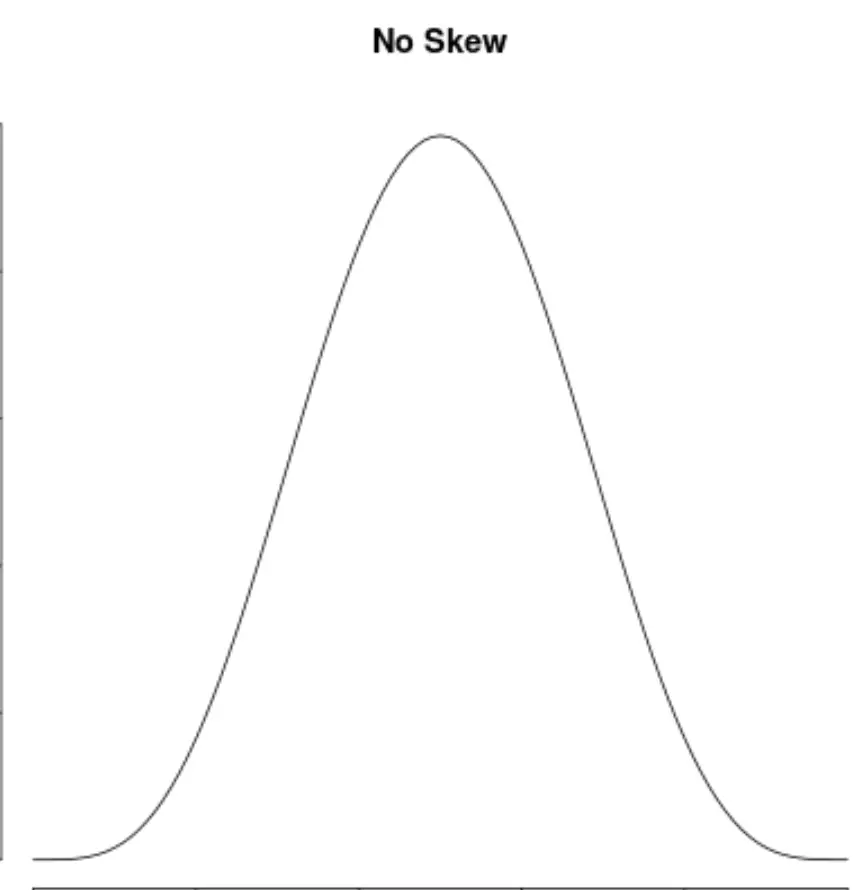
Hoe asymmetrie te interpreteren

De waarde van de asymmetrie kan variëren van negatief oneindig tot positief oneindig.

Zo interpreteert u de asymmetriewaarden:

• Een negatieve waarde voor scheefheid geeft aan dat de staart zich aan de linkerkant van de verdeling bevindt, die zich uitstrekt naar meer negatieve waarden.
• Een positieve waarde voor scheefheid geeft aan dat de staart zich aan de rechterkant van de verdeling bevindt, die zich uitstrekt naar meer positieve waarden.
• Een waarde nul geeft aan dat er geen asymmetrie in de verdeling is, wat betekent dat de verdeling perfect symmetrisch is.

De volgende voorbeelden laten zien hoe u asymmetriewaarden in de praktijk kunt interpreteren.

Voorbeeld 1: linksscheve verdeling

De leeftijdsverdeling van sterfgevallen is in de meeste populaties scheef naar links. De meeste mensen leven tussen de 70 en 80 jaar oud, en steeds minder mensen leven onder deze leeftijd.

Als we een dichtheidsplot zouden maken om de verdeling van waarden voor de leeftijd bij overlijden te visualiseren, zou het er als volgt uit kunnen zien:

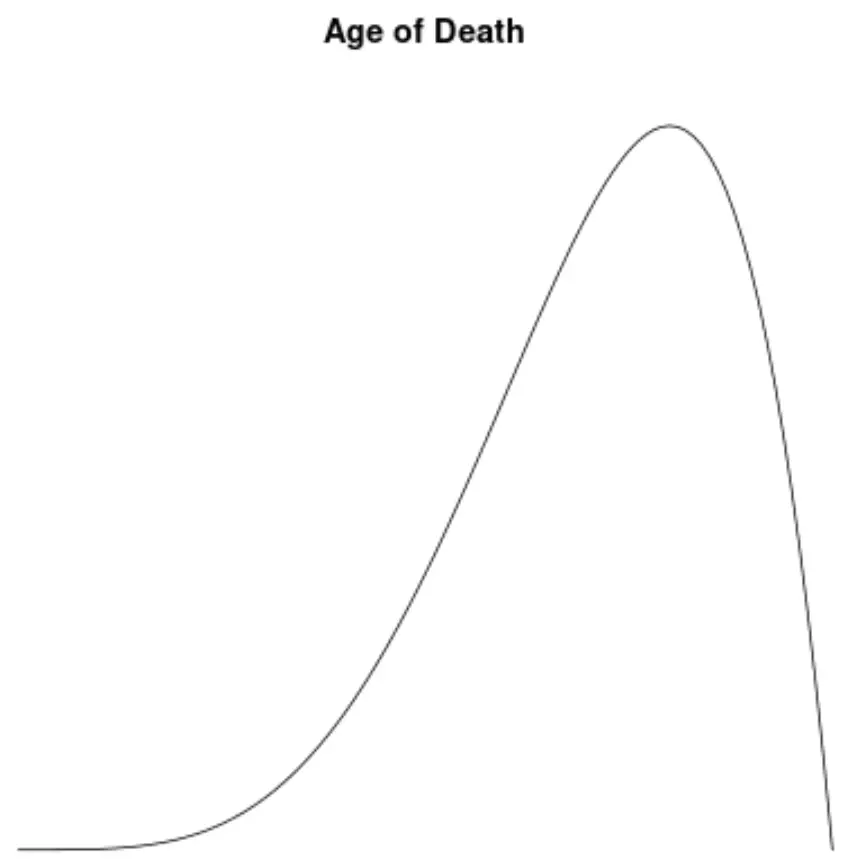
Stel dat we de scheefheid van deze verdeling berekenen en vaststellen dat deze -1,3225 is.

Omdat deze waarde negatief is, interpreteren we dit als een teken dat de verdeling linksscheef is, wat betekent dat de staart zich naar de linkerkant van de verdeling uitstrekt.

Voorbeeld 2: rechtsscheve verdeling

De verdeling van het gezinsinkomen in de Verenigde Staten is scheef naar rechts: de meeste huishoudens verdienen tussen de $30.000 en $70.000 per jaar, maar er is een lange rechterstaart van huishoudens die veel meer verdienen.

Als we een dichtheidsplot maken om de verdeling van de gezinsinkomenswaarden te visualiseren, zou het er als volgt uit kunnen zien:

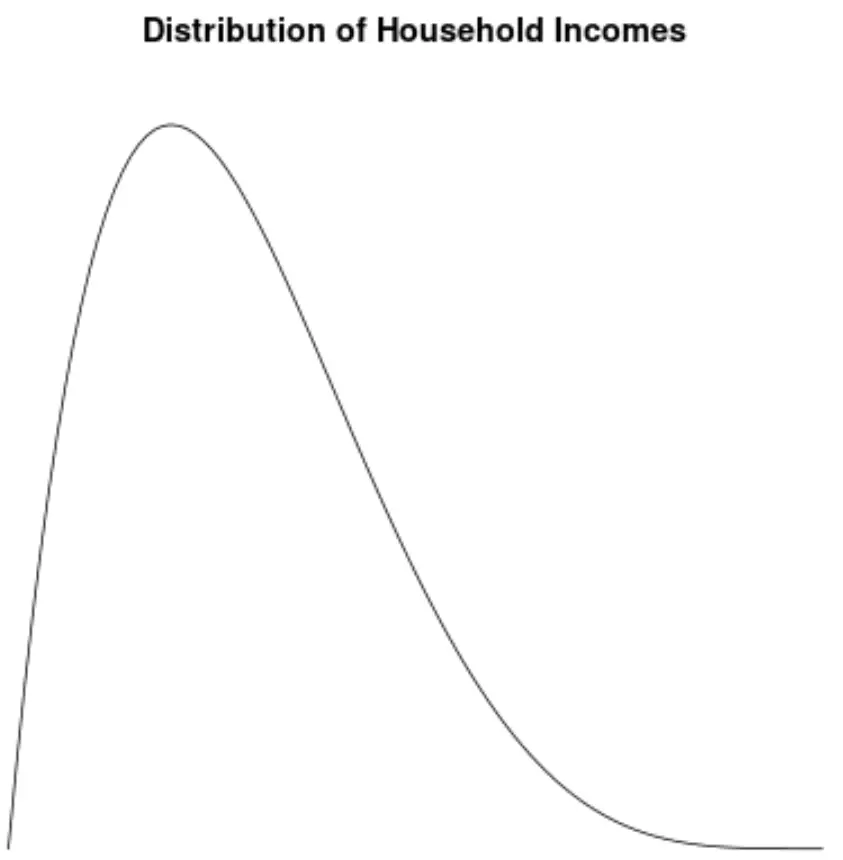
Stel dat we de scheefheid van deze verdeling berekenen en vaststellen dat deze 2,0043 is.

Omdat deze waarde positief is, interpreteren we dit als een teken dat de verdeling naar rechts scheef is, wat betekent dat de staart zich naar de rechterkant van de verdeling uitstrekt.

Voorbeeld 3: Geen vertekening

De grootte van mannen is ongeveer normaal verdeeld en vertoont geen asymmetrie. De gemiddelde lengte van een man in de Verenigde Staten is bijvoorbeeld ongeveer 69,1 inch. De hoogteverdeling is ruwweg symmetrisch, waarbij sommige korter en andere groter zijn.

Als we een dichtheidsdiagram zouden maken om de verdeling van mannelijke lengtes in de Verenigde Staten te visualiseren, zou het er als volgt uit kunnen zien:

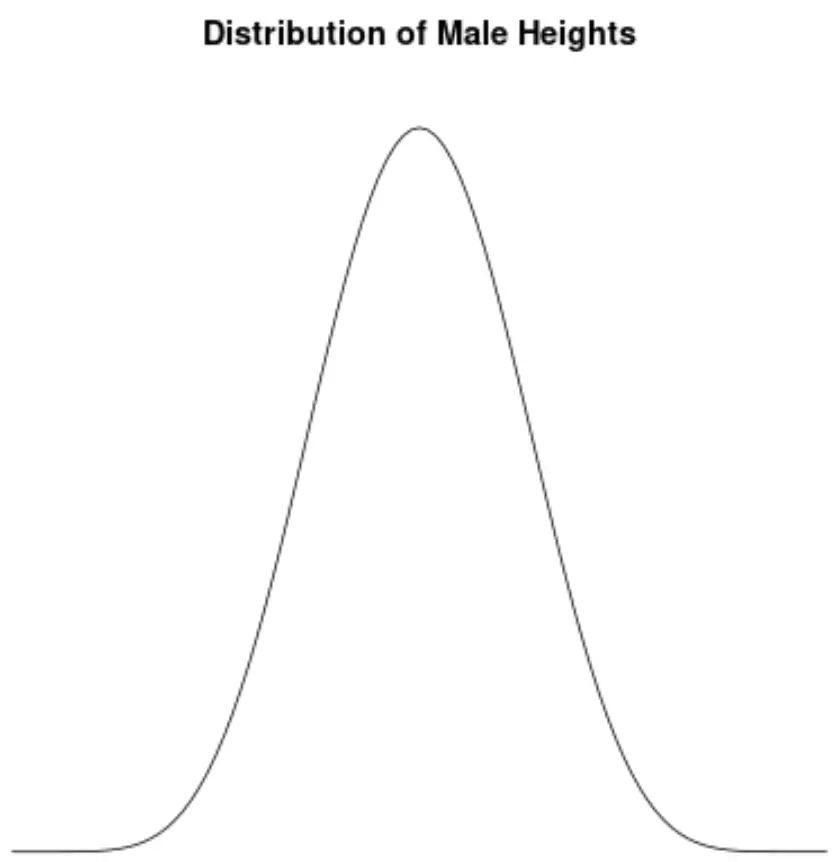
Stel dat we de scheefheid van deze verdeling berekenen en vaststellen dat deze 0,0013 is.

Omdat deze waarde bijna nul is, interpreteren we dit als een teken dat de verdeling vrijwel geen scheefheid vertoont, wat betekent dat de staarten aan weerszijden van de verdeling ongeveer gelijk zijn.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over scheve statistieken:

5 voorbeelden van positief scheve verdelingen
5 voorbeelden van negatief scheve verdelingen
Hoe scheefheid in Excel te berekenen
Hoe asymmetrie in boxplots te identificeren