Volledige gids: anova-resultaten interpreteren in sas

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

In het volgende voorbeeld ziet u hoe u de resultaten van een eenrichtings-ANOVA in SAS interpreteert.

Voorbeeld: ANOVA-resultaten interpreteren in SAS

Stel dat een onderzoeker 30 studenten recruteert om aan een onderzoek deel te nemen. Studenten worden willekeurig toegewezen om een van de drie studiemethoden te gebruiken ter voorbereiding op een examen.

Hieronder vindt u de examenresultaten per student:

We kunnen de volgende code gebruiken om deze gegevensset in SAS te maken:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Vervolgens zullen we proc ANOVA gebruiken om de eenrichtings-ANOVA uit te voeren:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

Opmerking : we gebruikten de middelenverklaring samen met de opties tukey en cldiff om te specificeren dat een post-hoc-test van Tukey moet worden uitgevoerd (met betrouwbaarheidsintervallen) als de totale p-waarde van de eenrichtings-ANOVA statistisch significant is.

Eerst kijken we naar de ANOVA-tabel in het resultaat:

Zo interpreteert u elke waarde in de uitvoer:

DF-model: de vrijheidsgraden voor de variabele methode . Dit wordt berekend als #groepen -1. In dit geval waren er 3 verschillende onderzoeksmethoden, dus deze waarde is: 3-1 = 2 .

DF-fout: de vrijheidsgraden voor de residuen. Dit wordt berekend als #totaal observaties – #groepen. In dit geval waren er 24 waarnemingen en 3 groepen, dus deze waarde is: 24-3 = 21 .

Gecorrigeerd totaal : de som van het DF-model en de DF-fout. Deze waarde is 2 + 21 = 23 .

Som van kwadratenmodel: De som van de kwadraten die is gekoppeld aan de variabelemethode . Deze waarde bedraagt 175,583 .

Som van kwadratenfout: Som van kwadraten geassocieerd met residuen of “fouten”. Deze waarde bedraagt 350,25 .

Gecorrigeerde som van kwadratentotaal : de som van het SS-model en de SS-fout. Deze waarde bedraagt 525,833 .

Gemiddelde kwadratenmodel: gemiddelde som van kwadraten geassocieerd met de methode . Dit wordt berekend als SS-model / DF-model, of 175,583 / 2 = 87,79 .

Gemiddelde kwadratische fout: gemiddelde som van kwadraten geassocieerd met de residuen. Dit wordt berekend als SS-fout / DF-fout, wat 350,25 / 21 = 16,68 is.

F-waarde: De algemene F-statistiek van het ANOVA-model. Dit wordt berekend als de gemiddelde kwadratische/gemiddelde kwadratische fout van het model, oftewel 87,79/16,68 = 5,26 .

Pr >F: de p-waarde die is gekoppeld aan de F-statistiek met teller df = 2 en noemer df = 21. In dit geval is de p-waarde 0,0140 .

De belangrijkste waarde in de reeks resultaten is de p-waarde, omdat deze ons vertelt of er een significant verschil is in de gemiddelde waarden tussen de drie groepen.

Bedenk dat een eenrichtings-ANOVA de volgende nul- en alternatieve hypothesen gebruikt:

• H ₀ (nulhypothese): alle groepsgemiddelden zijn gelijk.
• _HA (alternatieve hypothese): Ten minste één groepsgemiddelde verschilt van de andere.

Omdat de p-waarde in onze ANOVA-tabel (0,0140) kleiner is dan 0,05, verwerpen we de nulhypothese.

Dit betekent dat we voldoende bewijs hebben om te zeggen dat de gemiddelde examenscore niet gelijk is over de drie studiemethoden.

Om precies te bepalen welke groepsgemiddelden verschillend zijn, moeten we de tabel met uiteindelijke resultaten raadplegen, die de resultaten van de post-hoc-tests van Tukey toont:

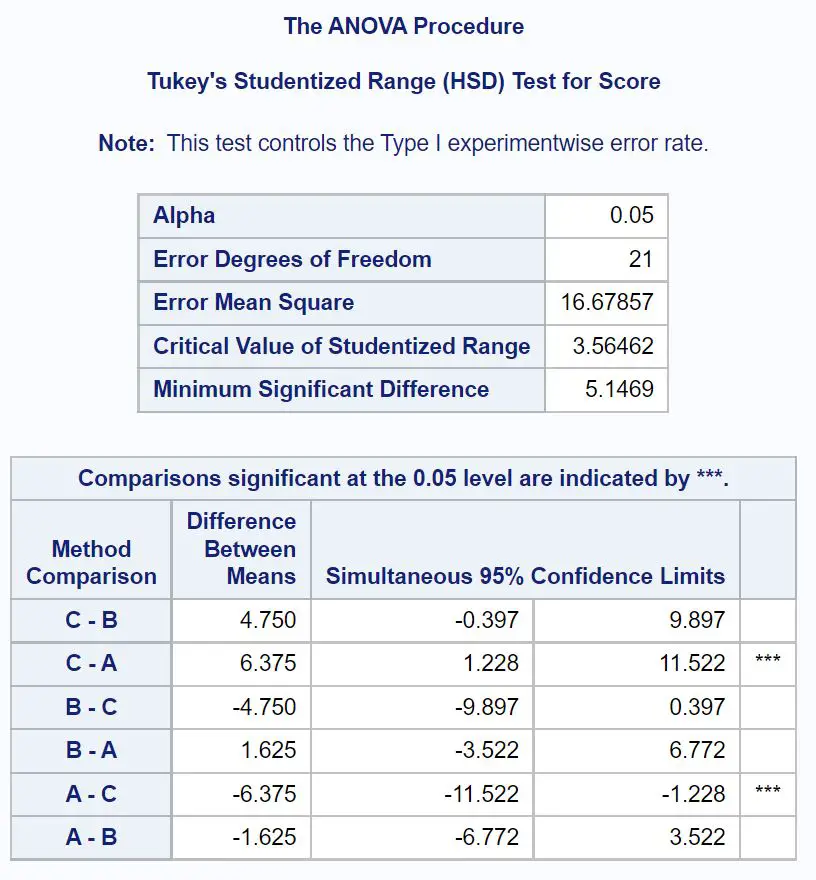
Om erachter te komen welke groepsgemiddelden verschillend zijn, moeten we kijken naar welke paarsgewijze vergelijkingen sterren ( *** ) ernaast hebben.

Uit de tabel blijkt dat er een statistisch significant verschil is in de gemiddelde examenscores tussen Groep A en Groep C.

Concreet bedraagt het gemiddelde verschil in examenscores tussen Groep C en Groep A 6,375 .

Het 95% betrouwbaarheidsinterval voor het gemiddelde verschil is [1,228; 11,522] .

Er zijn geen statistisch significante verschillen tussen de gemiddelden van de andere groepen.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over ANOVA-modellen:

Een gids voor het gebruik van post-hoctesten met ANOVA
Eenrichtings-ANOVA uitvoeren in SAS
Hoe u tweerichtings-ANOVA uitvoert in SAS