Een roc-curve interpreteren (met voorbeelden)

Logistische regressie is een statistische methode die we gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is. Om te evalueren hoe goed een logistisch regressiemodel bij een dataset past, kunnen we naar de volgende twee statistieken kijken:

• Gevoeligheid: waarschijnlijkheid dat het model een positief resultaat voorspelt voor een waarneming terwijl het resultaat daadwerkelijk positief is.
• Specificiteit: waarschijnlijkheid dat het model een negatief resultaat voorspelt voor een waarneming terwijl het resultaat feitelijk negatief is.

Een eenvoudige manier om deze twee statistieken te visualiseren is door een ROC-curve te maken, een grafiek die de gevoeligheid en specificiteit van een logistisch regressiemodel weergeeft.

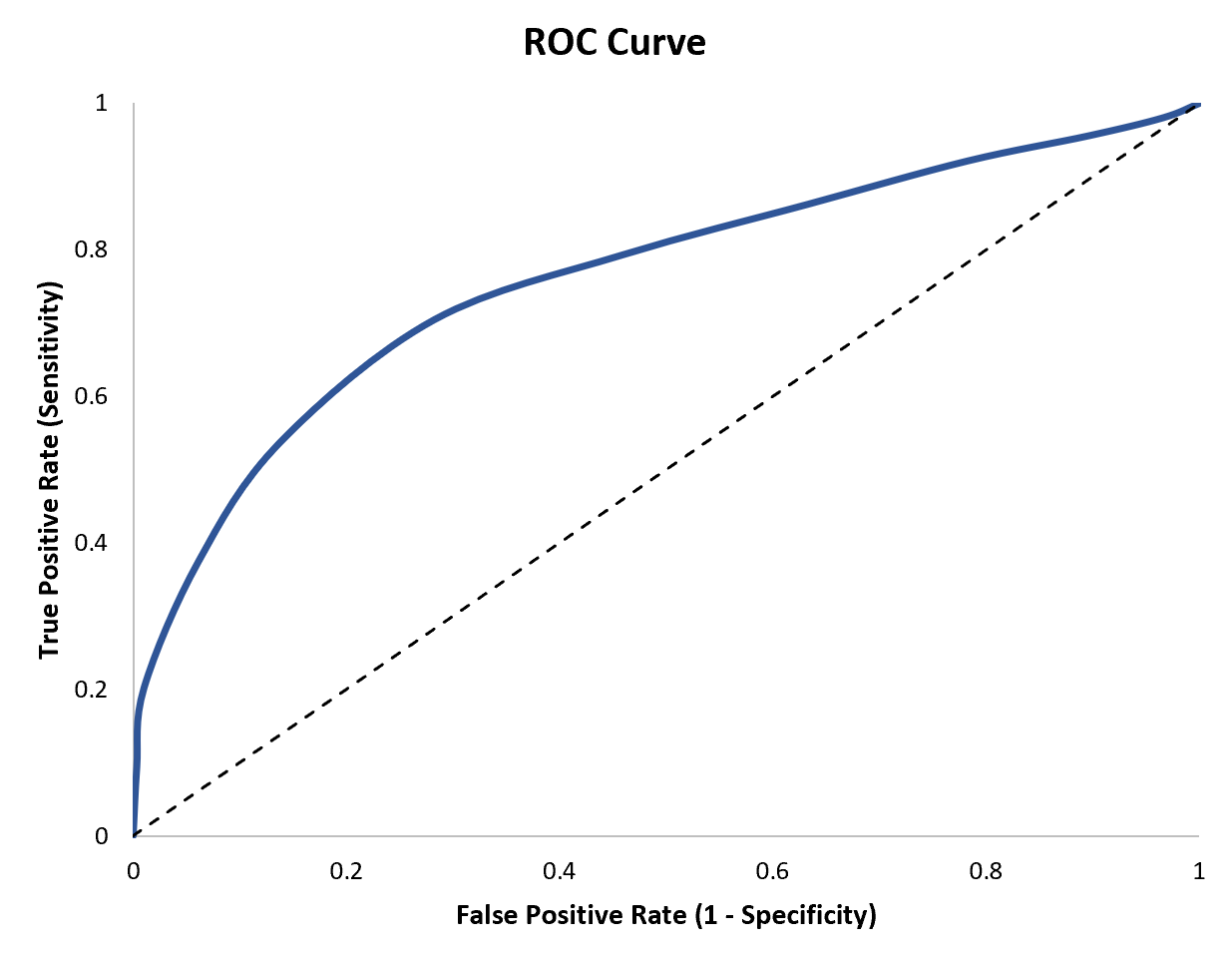
In deze tutorial wordt uitgelegd hoe u een ROC-curve maakt en interpreteert.

Hoe u een ROC-curve maakt

Zodra we een logistisch regressiemodel hebben geïnstalleerd, kunnen we het model gebruiken om waarnemingen in een van de twee categorieën te classificeren.

We kunnen waarnemingen bijvoorbeeld classificeren als ‘positief’ of ‘negatief’.

Het werkelijk positieve percentage vertegenwoordigt het aandeel waarnemingen dat positief zou moeten zijn, terwijl ze dat in werkelijkheid ook zijn.

Omgekeerd vertegenwoordigt het percentage fout-positieve waarnemingen het aandeel waarnemingen dat positief zou moeten zijn, maar in werkelijkheid negatief is.

Wanneer we een ROC-curve maken, zetten we de paren van echt positieve percentages versus fout-positieve percentages uit voor elke mogelijke beslissingsdrempel van een logistisch regressiemodel.

Hoe een ROC-curve te interpreteren

Hoe dichter de ROC-curve bij de linkerbovenhoek van de grafiek past, hoe beter het model de gegevens in categorieën kan indelen.

Om dit te kwantificeren, kunnen we de AUC (oppervlakte onder de curve) berekenen, die ons vertelt hoeveel van de grafiek zich onder de curve bevindt.

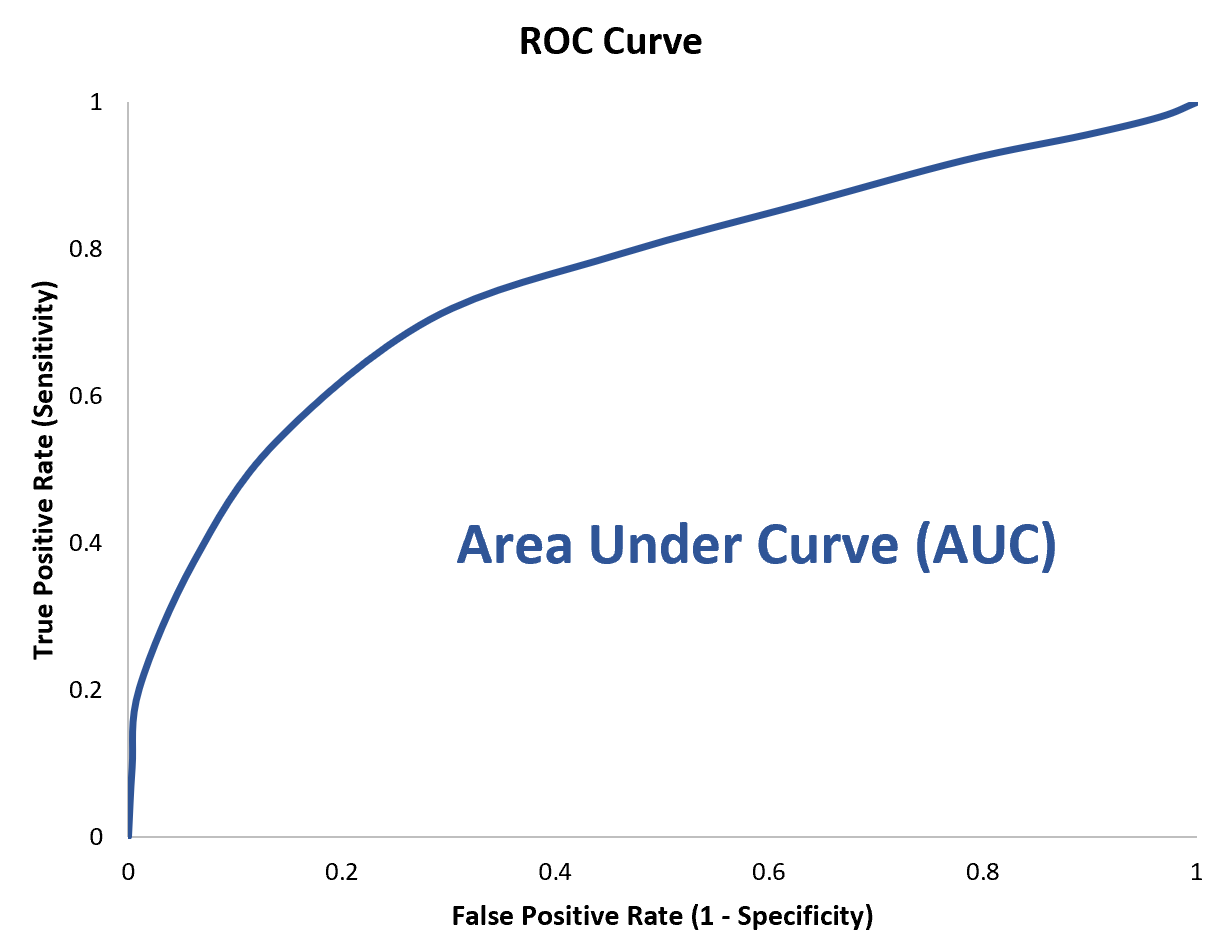
Hoe dichter de AUC bij 1 ligt, hoe beter het model.

Een model met een AUC gelijk aan 0,5 zou een perfect diagonale lijn zijn en zou een model vertegenwoordigen dat niet beter is dan een model dat willekeurige classificaties uitvoert.

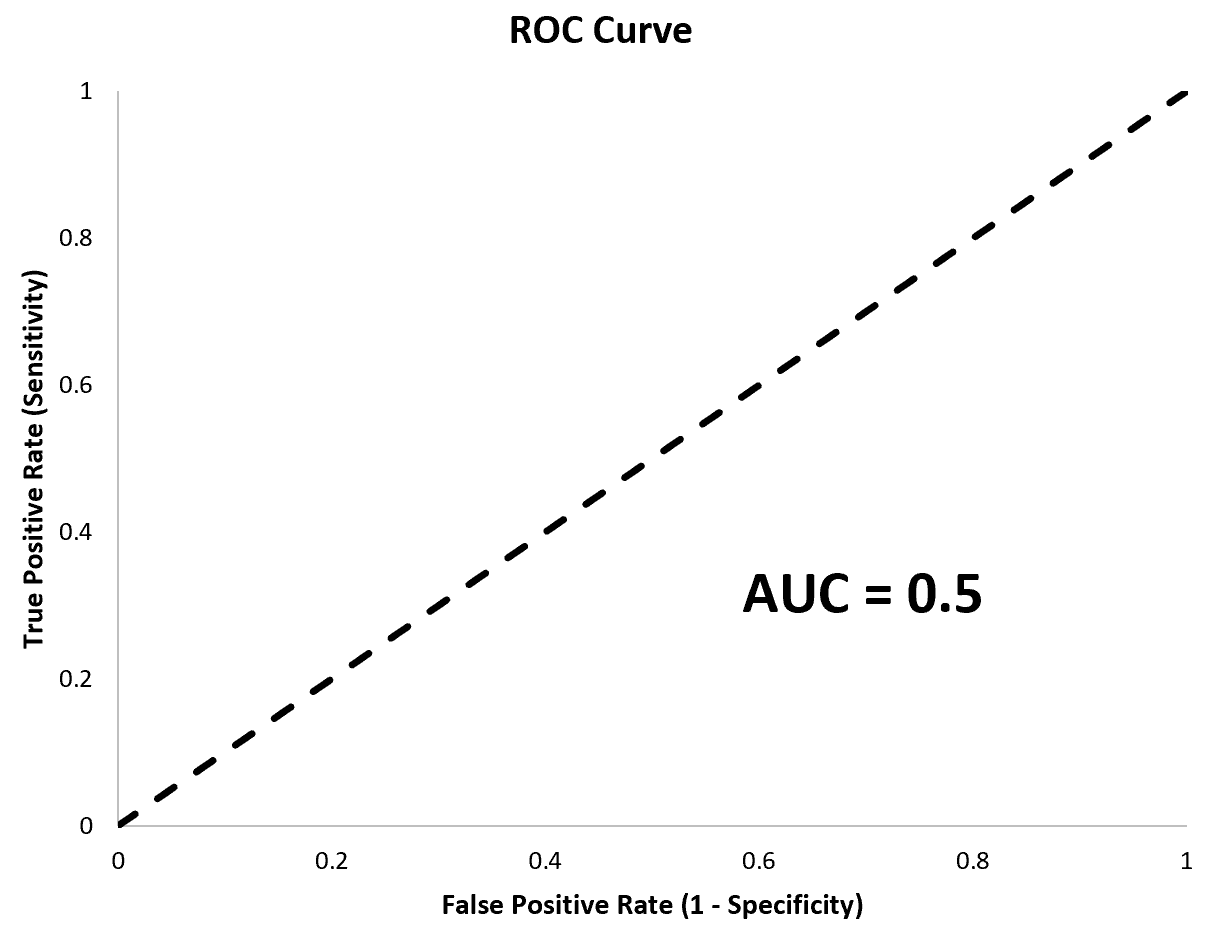
Het is met name handig om de AUC voor meerdere logistieke regressiemodellen te berekenen, omdat we hierdoor kunnen zien welk model het beste voorspellingen kan doen.

Stel dat we drie verschillende logistieke regressiemodellen passen en voor elk model de volgende ROC-curven uitzetten:

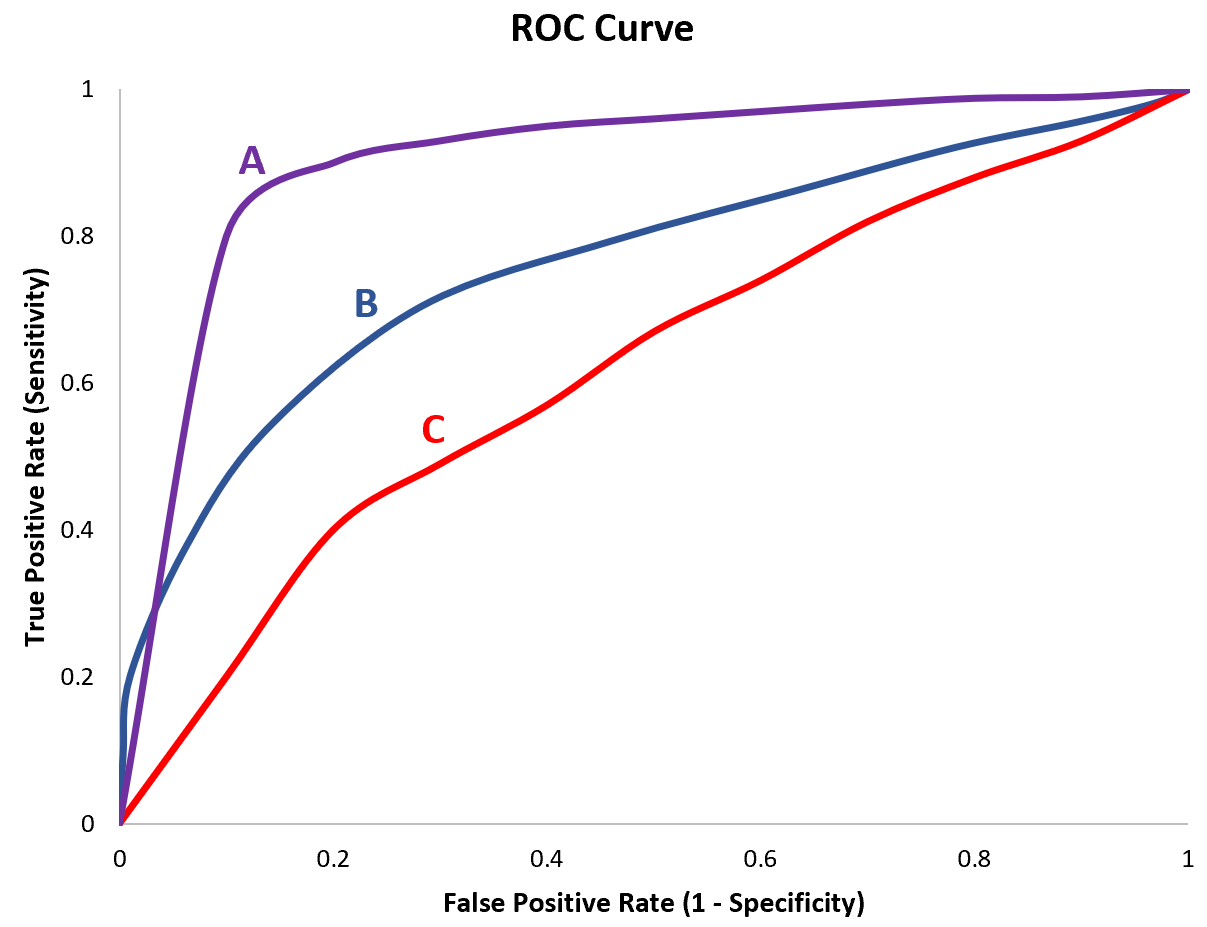
Stel dat we de AUC voor elk model als volgt berekenen:

• Model A: AUC = 0,923
• Model B: AUC = 0,794
• Model C: AUC = 0,588

Model A heeft de hoogste AUC, wat aangeeft dat het het hoogste gebied onder de curve heeft en het beste model is voor het correct indelen van waarnemingen in categorieën.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u ROC-curven kunt maken met behulp van verschillende statistische software:

• Hoe een ROC-curve in R te plotten
• Hoe een ROC-curve in Python te plotten
• Hoe u een ROC-curve in Excel maakt
• Hoe u een ROC-curve in SPSS kunt maken en interpreteren
• Hoe u een ROC-curve in Stata maakt en interpreteert