Volledige gids: anova-resultaten interpreteren in excel

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Het volgende voorbeeld biedt een volledige handleiding voor het interpreteren van de resultaten van een eenrichtings-ANOVA in Excel.

Voorbeeld: ANOVA-resultaten interpreteren in Excel

Stel dat een leraar willekeurig 30 leerlingen in zijn klas vraagt om een van de drie studiemethoden te gebruiken ter voorbereiding op een examen.

De volgende schermafbeelding toont de scores van studenten op basis van de methode die ze hebben gebruikt:

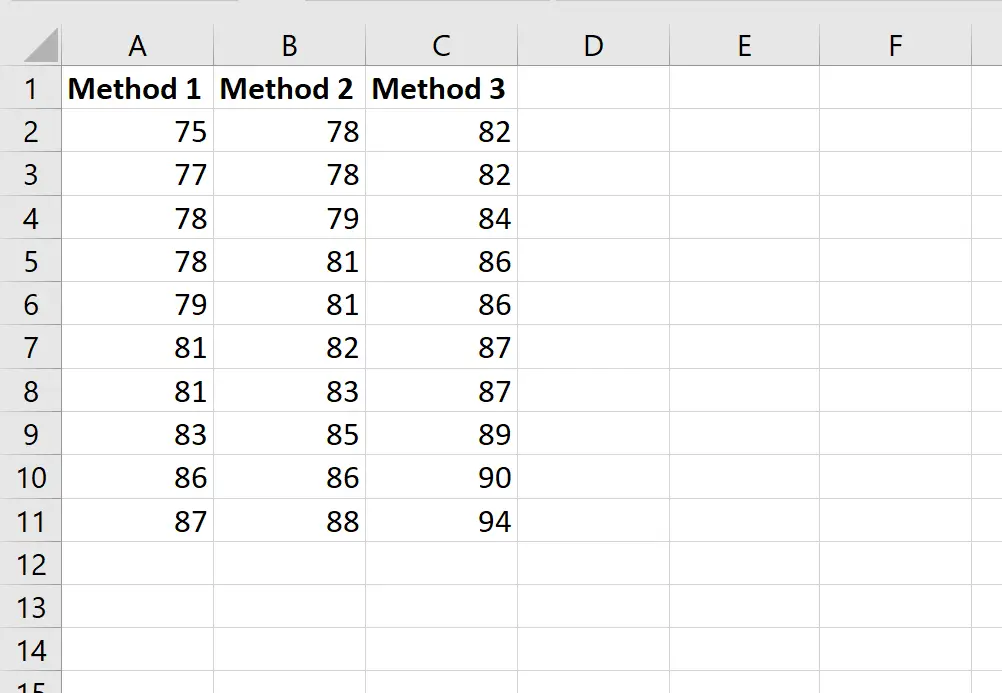
Stel dat de docent een one-way ANOVA wil uitvoeren om te bepalen of de gemiddelde scores voor de drie groepen hetzelfde zijn.

Als u een eenrichtings-ANOVA in Excel wilt uitvoeren, klikt u op het tabblad Gegevens op het bovenste lint en klikt u vervolgens op Gegevensanalyse in de groep Analyseren .

Als u de optie Data Analysis niet ziet , moet u eerst de gratis Analysis ToolPak- software laden.

Zodra u erop klikt, verschijnt er een nieuw venster. Selecteer Anova: Single Factor en klik vervolgens op OK .

In het nieuwe venster dat verschijnt, voert u de volgende gegevens in:

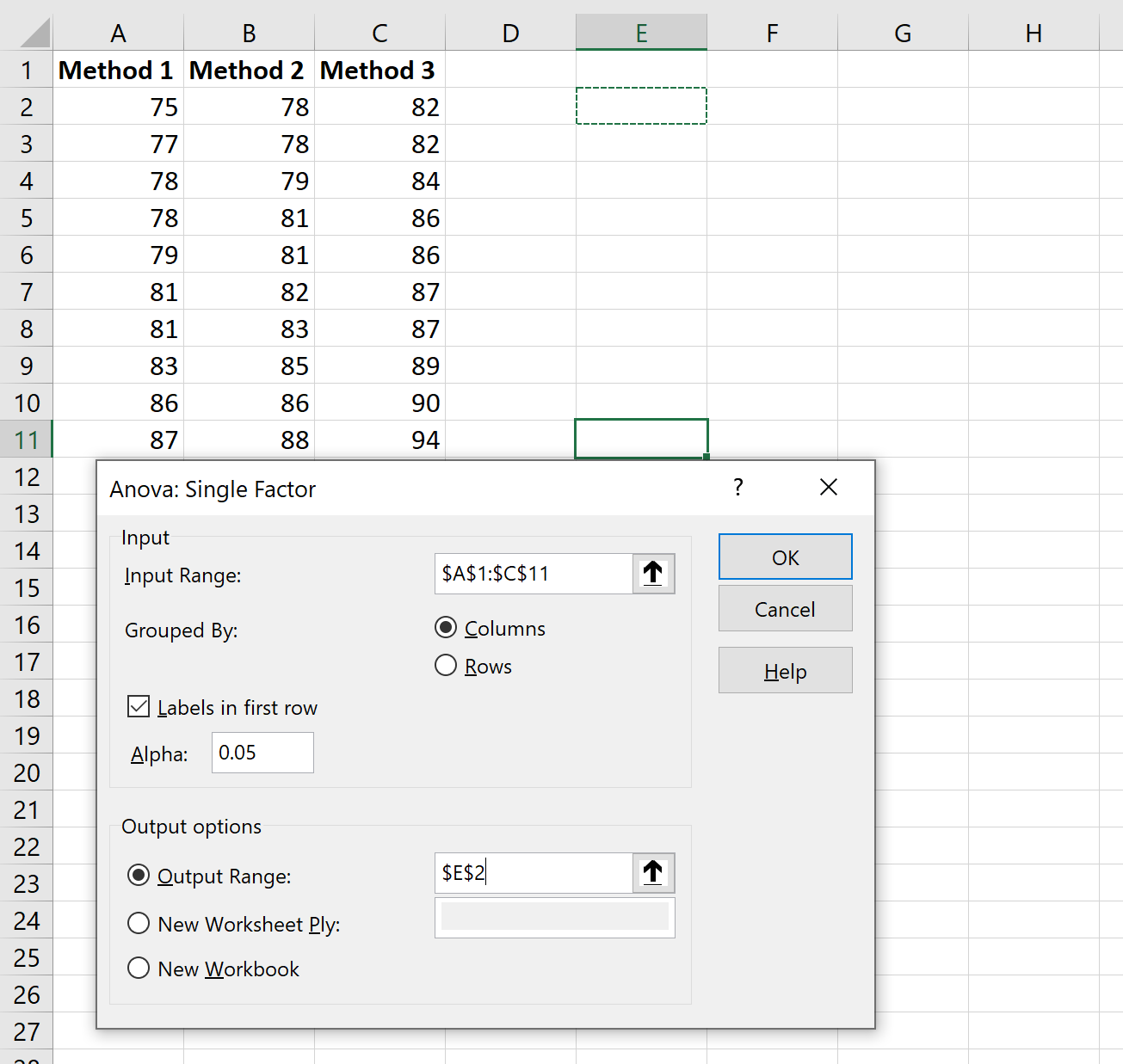
Zodra u op OK klikt, verschijnen de eenrichtings-ANOVA-resultaten:

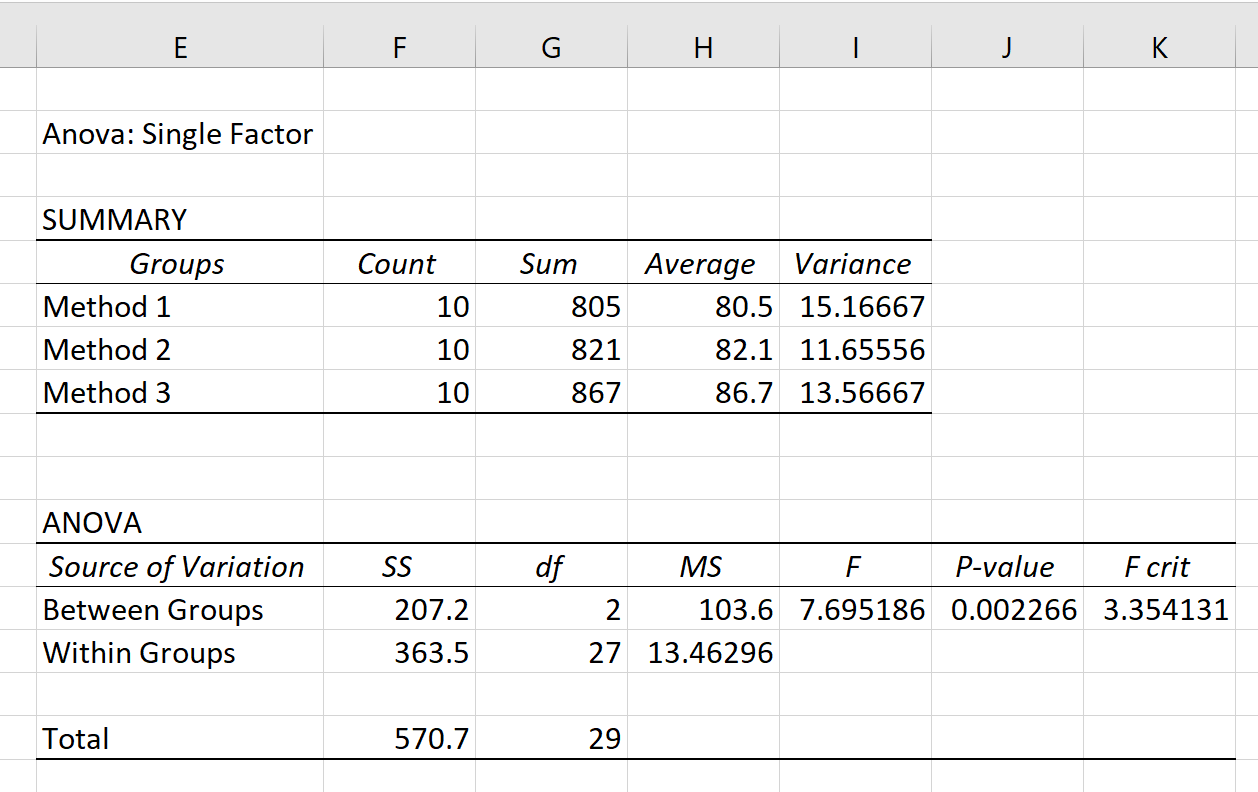
In het resultaat worden twee tabellen weergegeven: SUMMARY en ANOVA .

Zo interpreteert u de waarden in elke tabel:

SAMENVATTING tabel :

• Groepen : groepsnamen
• Aantal : het aantal observaties in elke groep
• Som : De som van de waarden van elke groep
• Gemiddelde : de gemiddelde waarde in elke groep
• Variantie : De variantie van de waarden in elke groep

Deze tabel biedt ons verschillende nuttige samenvattende statistieken voor elke groep die in de ANOVA wordt gebruikt.

Uit deze tabel kunnen we zien dat studenten die methode 3 gebruikten de hoogste gemiddelde examenscore hadden (86,7), maar ook de hoogste variantie in testscores hadden. beoordeling (13.56667).

Om te bepalen of de verschillen in groepsgemiddelden statistisch significant zijn, moeten we de ANOVA-tabel raadplegen.

ANOVA-tabel :

• Bron van variatie : de gemeten variatie (tussen groepen of binnen groepen)
• SS : De som van de kwadraten voor elke bron van variatie
• df : De vrijheidsgraden, berekend als #groups-1 voor df Between en #observations – #groups voor df Within
• MS : De gemiddelde som van de kwadraten, berekend in SS/df
• F : De totale F-waarde, berekend als MS Between / MS Within
• P-waarde : de p-waarde die overeenkomt met de totale F-waarde
• F crit : De kritische waarde F die overeenkomt met α = 0,05

De belangrijkste waarde in deze tabel is de p-waarde , die 0,002266 blijkt te zijn.

Bedenk dat een eenrichtings-ANOVA de volgende nul- en alternatieve hypothesen gebruikt:

• H ₀ : Alle groepsgemiddelden zijn gelijk.
• H _A : Niet alle groepsgemiddelden zijn gelijk.

Omdat de p-waarde kleiner is dan α = 0,05, verwerpen we de nulhypothese van eenrichtings-ANOVA en concluderen we dat we voldoende bewijs hebben om te stellen dat niet alle groepsgemiddelden gelijk zijn.

Dit betekent dat niet alle drie de studievormen tot dezelfde gemiddelde examencijfers leiden.

Opmerking : u kunt ook de algehele F-waarde vergelijken met de kritische F-waarde om te bepalen of u de nulhypothese wel of niet moet verwerpen. In dit geval zouden we de nulhypothese verwerpen, aangezien de totale waarde van F groter is dan de kritische waarde van F. Merk op dat de p-waardebenadering en de kritische F-waardebenadering altijd tot dezelfde conclusie zullen leiden.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u verschillende ANOVA’s in Excel kunt uitvoeren:

Eenrichtings-ANOVA uitvoeren in Excel
Een tweerichtings-ANOVA uitvoeren in Excel
Hoe herhaalde metingen ANOVA in Excel uit te voeren
Geneste ANOVA uitvoeren in Excel