K-means clustering in python: stapsgewijs voorbeeld

Een van de meest voorkomende clusteralgoritmen bij machinaal leren staat bekend als k-means clustering .

K-means clustering is een techniek waarbij we elke waarneming uit een dataset in een van de K- clusters plaatsen.

Het einddoel is om K- clusters te hebben waarin waarnemingen binnen elke cluster behoorlijk op elkaar lijken, terwijl waarnemingen in verschillende clusters behoorlijk van elkaar verschillen.

In de praktijk gebruiken we de volgende stappen om K-means clustering uit te voeren:

1. Kies een waarde voor K.

• Eerst moeten we beslissen hoeveel clusters we in de gegevens willen identificeren. Vaak hoeven we eenvoudigweg verschillende waarden voor K te testen en de resultaten te analyseren om te zien welk aantal clusters het meest logisch lijkt voor een bepaald probleem.

2. Wijs elke waarneming willekeurig toe aan een eerste cluster, van 1 tot K.

3. Voer de volgende procedure uit totdat de clustertoewijzingen niet meer veranderen.

• Bereken voor elk van de K- clusters het zwaartepunt van het cluster. Dit is eenvoudigweg de vector van p- gemiddelde kenmerken voor de waarnemingen van de k- de cluster.
• Wijs elke waarneming toe aan het cluster met het dichtstbijzijnde zwaartepunt. Hier wordt de dichtstbijzijnde gedefinieerd met behulp van de Euclidische afstand .

Het volgende stapsgewijze voorbeeld laat zien hoe u k-means-clustering in Python kunt uitvoeren met behulp van de KMeans- functie van de sklearn- module.

Stap 1: Importeer de benodigde modules

Eerst zullen we alle modules importeren die we nodig hebben om k-means clustering uit te voeren:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Stap 2: Maak het DataFrame

Vervolgens maken we een DataFrame met de volgende drie variabelen voor 20 verschillende basketbalspelers:

• punten
• hulp
• stuitert

De volgende code laat zien hoe u dit panda’s DataFrame maakt:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

We zullen k-means-clustering gebruiken om vergelijkbare actoren te groeperen op basis van deze drie metrieken.

Stap 3: Maak het DataFrame schoon en bereid het voor

Vervolgens voeren wij de volgende stappen uit:

• Gebruik dropna() om rijen met NaN-waarden in elke kolom neer te zetten
• Gebruik StandardScaler() om elke variabele te schalen zodat deze een gemiddelde van 0 en een standaarddeviatie van 1 heeft.

De volgende code laat zien hoe u dit doet:

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

Opmerking : we gebruiken schaling zodat elke variabele even belangrijk is bij het aanpassen van het k-means-algoritme. Anders zouden de variabelen met het grootste bereik te veel invloed hebben.

Stap 4: Vind het optimale aantal clusters

Om k-means-clustering in Python uit te voeren, kunnen we de KMeans- functie van de sklearn- module gebruiken.

Deze functie gebruikt de volgende basissyntaxis:

KMeans(init=’willekeurig‘, n_clusters=8, n_init=10, random_state=Geen)

Goud:

• init : Beheert de initialisatietechniek.
• n_clusters : het aantal clusters waarin de waarnemingen moeten worden geplaatst.
• n_init : Het aantal uit te voeren initialisaties. De standaardinstelling is om het k-means-algoritme 10 keer uit te voeren en het algoritme met de laagste SSE te retourneren.
• random_state : Een geheel getalwaarde die u kunt kiezen om de algoritmeresultaten reproduceerbaar te maken.

Het belangrijkste argument voor deze functie is n_clusters, dat specificeert in hoeveel clusters waarnemingen moeten worden geplaatst.

We weten echter niet van tevoren hoeveel clusters optimaal zijn, dus moeten we een grafiek maken die het aantal clusters weergeeft, evenals de SSE (som van kwadratische fouten) van het model.

Wanneer we dit type plot maken, zoeken we doorgaans naar een ‘knie’ waar de som van de vierkanten begint te ‘buigen’ of af te vlakken. Dit is doorgaans het optimale aantal clusters.

De volgende code laat zien hoe u dit type plot maakt, waarin het aantal clusters op de x-as en de SSE op de y-as wordt weergegeven:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

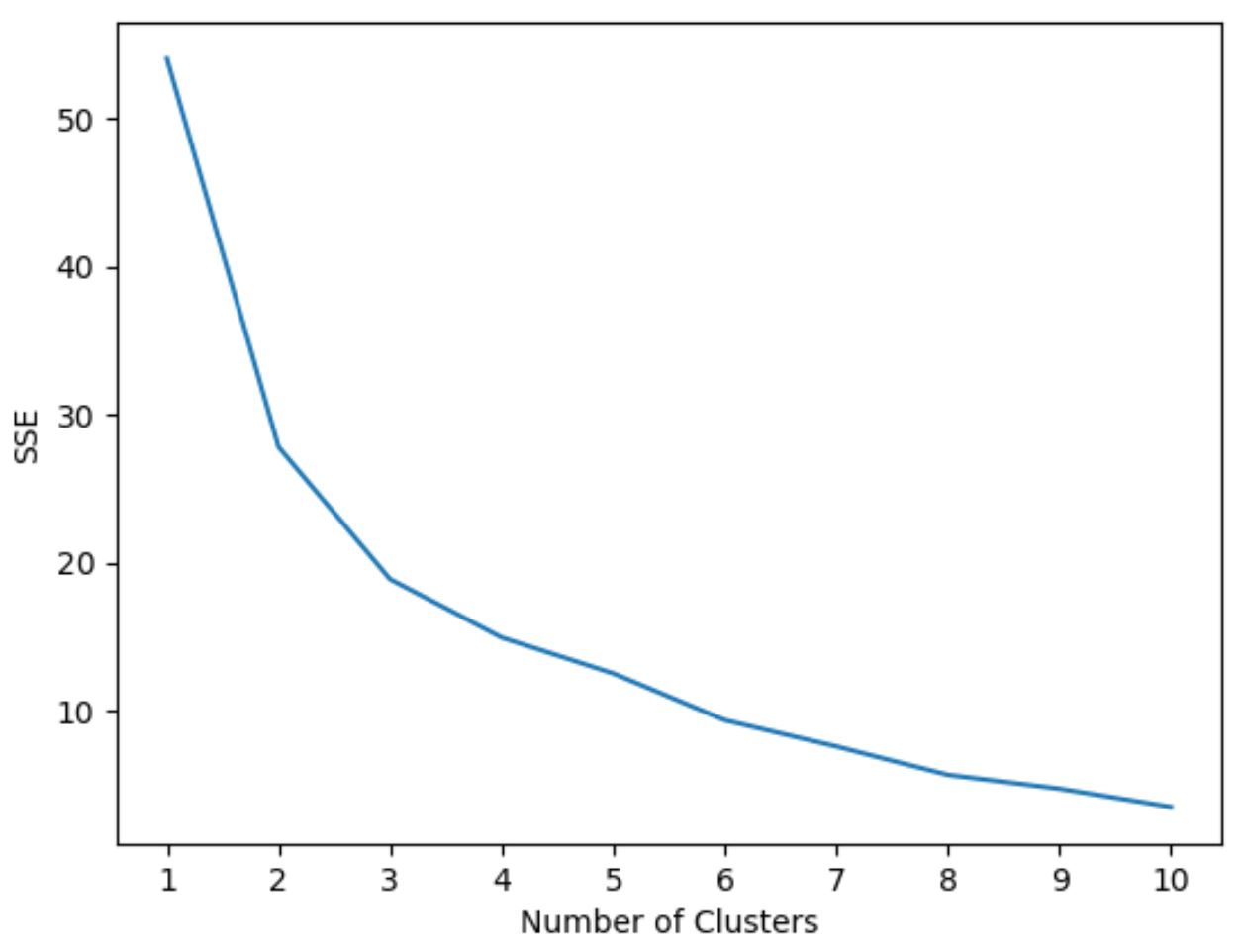
In deze grafiek lijkt het erop dat er een knik of „knie“ is bij k = 3 clusters .

We zullen dus 3 clusters gebruiken bij het aanpassen van ons k-means clusteringmodel in de volgende stap.

Opmerking : in de echte wereld wordt aanbevolen om een combinatie van deze plot- en domeinexpertise te gebruiken om het aantal te gebruiken clusters te kiezen.

Stap 5: Voer K-Means Clustering uit met Optimal K

De volgende code laat zien hoe u k-means-clustering op de dataset uitvoert met behulp van de optimale waarde voor k van 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

De resulterende tabel toont de clustertoewijzingen voor elke waarneming in het DataFrame.

Om deze resultaten gemakkelijker te kunnen interpreteren, kunnen we een kolom aan het DataFrame toevoegen waarin de clustertoewijzing van elke speler wordt weergegeven:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

De clusterkolom bevat een clusternummer (0, 1 of 2) waaraan elke speler is toegewezen.

Spelers die tot hetzelfde cluster behoren, hebben ongeveer vergelijkbare waarden voor de kolommen punten , assists en rebounds .

Opmerking : u kunt hier de volledige documentatie voor de KMeans- functie van sklearn vinden.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in Python kunt uitvoeren:

Hoe lineaire regressie uit te voeren in Python
Hoe logistieke regressie uit te voeren in Python
Hoe K-Fold kruisvalidatie uit te voeren in Python