Chauvenet criterium: definitie en voorbeeld

Een uitschieter is een waarneming die abnormaal ver verwijderd is van andere waarden in een dataset. Uitschieters kunnen problematisch zijn omdat ze de resultaten van een analyse kunnen beïnvloeden.

Eén manier om uitschieters in een dataset te identificeren is door het Chauvenet-criterium te gebruiken, dat het volgende proces gebruikt:

1. Bereken voor elke individuele waarde x _i in de dataset de afwijking van het gemiddelde als volgt:

Afwijking = |x _i – x | /S

waarbij x het steekproefgemiddelde is en s de standaarddeviatie van de steekproef.

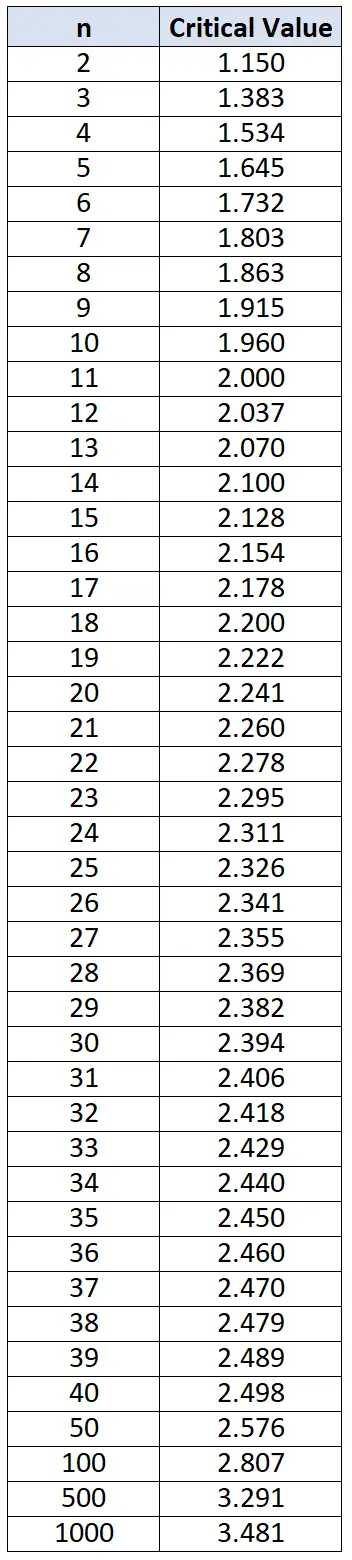
2. Vergelijk de afwijkingen van elke individuele waarde met de kritische waarden in de Chauvenet-criteriatabel hieronder. Voor individuele gegevenswaarden met afwijkingen die groter zijn dan die in de tabel, rapporteert u deze gegevenswaarden als uitschieters.

Het Chauvenet-criterium: een voorbeeld

Stel dat we de volgende gegevensset van 15 waarden hebben:

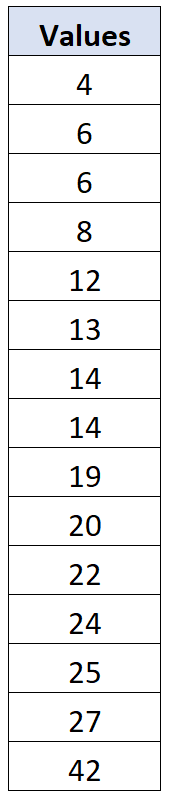
Het steekproefgemiddelde voor deze gegevensset is x = 17,067 en de standaarddeviatie van de steekproef is s = 10,096 . Voor elke individuele gegevenswaarde kunnen we de afwijking als volgt berekenen:

Afwijking = |x _i – x | /S

Bijvoorbeeld:

• De eerste gegevenswaarde zou een afwijking hebben van |4 – 17.067| / 10.096 = 1.294 .
• De eerste gegevenswaarde zou een afwijking hebben van |6 – 17,067| / 10,096 = 1,096 .

Enzovoort.

We kunnen dezelfde formule gebruiken om de afwijking van elke individuele gegevenswaarde te berekenen:

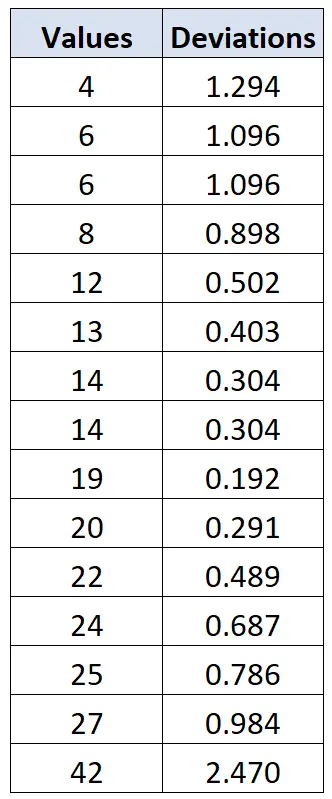
We kunnen dan naar de Chauvenet-criteriatabel verwijzen en vaststellen dat de kritische waarde die overeenkomt met een steekproefomvang van n=15 2,128 is. Elke waarde met een afwijking groter dan 2,128 kan dus als een uitbijter worden beschouwd.

Het blijkt dat de waarde 42 een afwijking heeft groter dan 2,128:

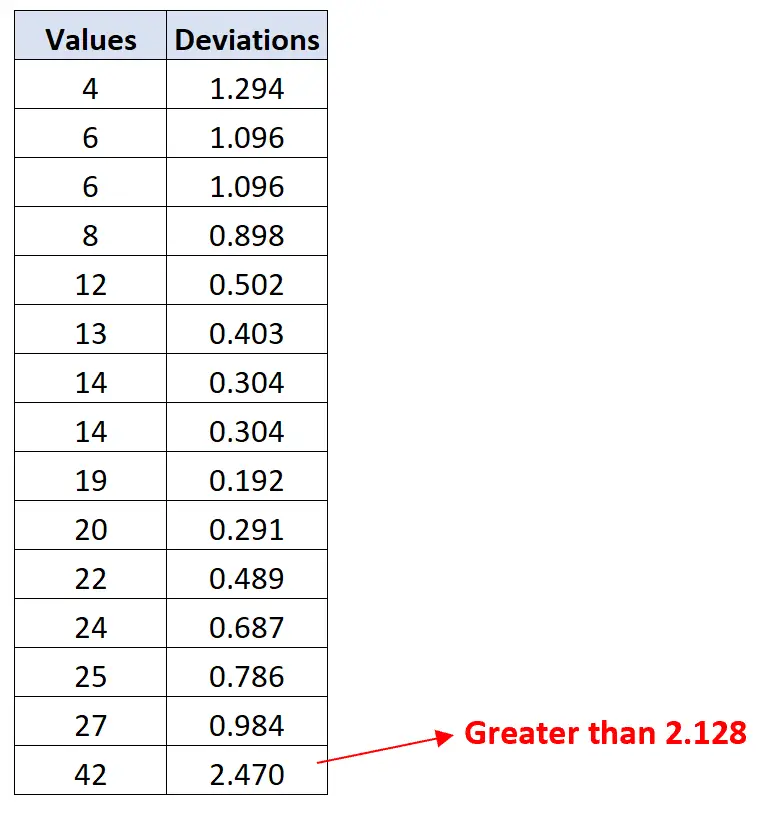
De waarde 42 is dus de enige uitschieter in deze dataset.

Voorzorgsmaatregelen met betrekking tot het gebruik van het Chauvenet-criterium

Het Chauvenet-criterium gaat ervan uit dat de waarden in een datasetnormaal verdeeld zijn. Als niet aan deze veronderstelling wordt voldaan, is het gebruik van het Chauvenet-criterium om uitschieters te identificeren waarschijnlijk niet geldig.

Als u deze methode gebruikt en constateert dat een waarde een uitbijter is, moet u eerst verifiëren dat de waarde niet het resultaat is van een gegevensinvoerfout. Soms worden gegevens simpelweg verkeerd ingevoerd.

Als de waarde echt een uitbijter is, kunt u ervoor kiezen deze te verwijderen als deze een aanzienlijke impact heeft op uw algehele analyse. Zorg ervoor dat u bij het rapporteren van uw resultaten vermeldt dat u een uitschieter heeft verwijderd.

Bovendien mag deze methode slechts één keer op een bepaalde dataset worden gebruikt. Stel dat we dit criterium bijvoorbeeld gebruiken om de waarde 42 in het vorige voorbeeld als een uitschieter te identificeren en die waarde uit de gegevensset te verwijderen.

We moeten dan het steekproefgemiddelde en de standaarddeviatie niet opnieuw berekenen en de afwijkingen opnieuw berekenen om meer uitschieters te vinden.