Kan kurtosis negatief zijn?

In de statistiek wordt kurtosis gebruikt om de vorm van een waarschijnlijkheidsverdeling te beschrijven.

Concreet vertelt het ons hoe goed datawaarden clusteren in de staarten of bovenaan een distributie.

De kurtosis van een verdeling kan negatief, nul of positief zijn.

Nul Kurtosis

Als een verdeling een kurtosis van 0 heeft, dan is deze gelijk aan de normale verdeling die de volgende belvorm heeft:

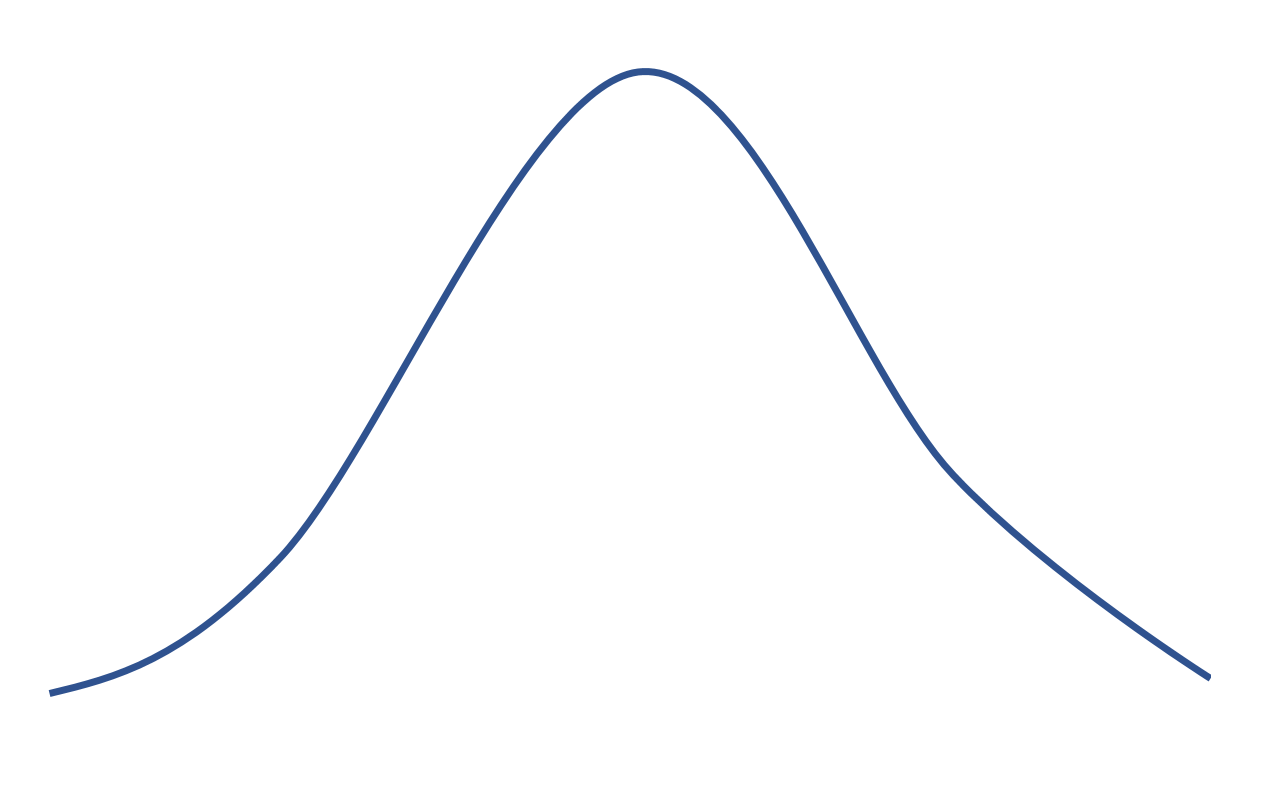
Positieve kurtosis

Als een verdeling positieve kurtosis heeft, wordt er gezegd dat deze leptokurtisch is, wat betekent dat de verdeling een scherpere piek en zwaardere staarten heeft vergeleken met een normale verdeling.

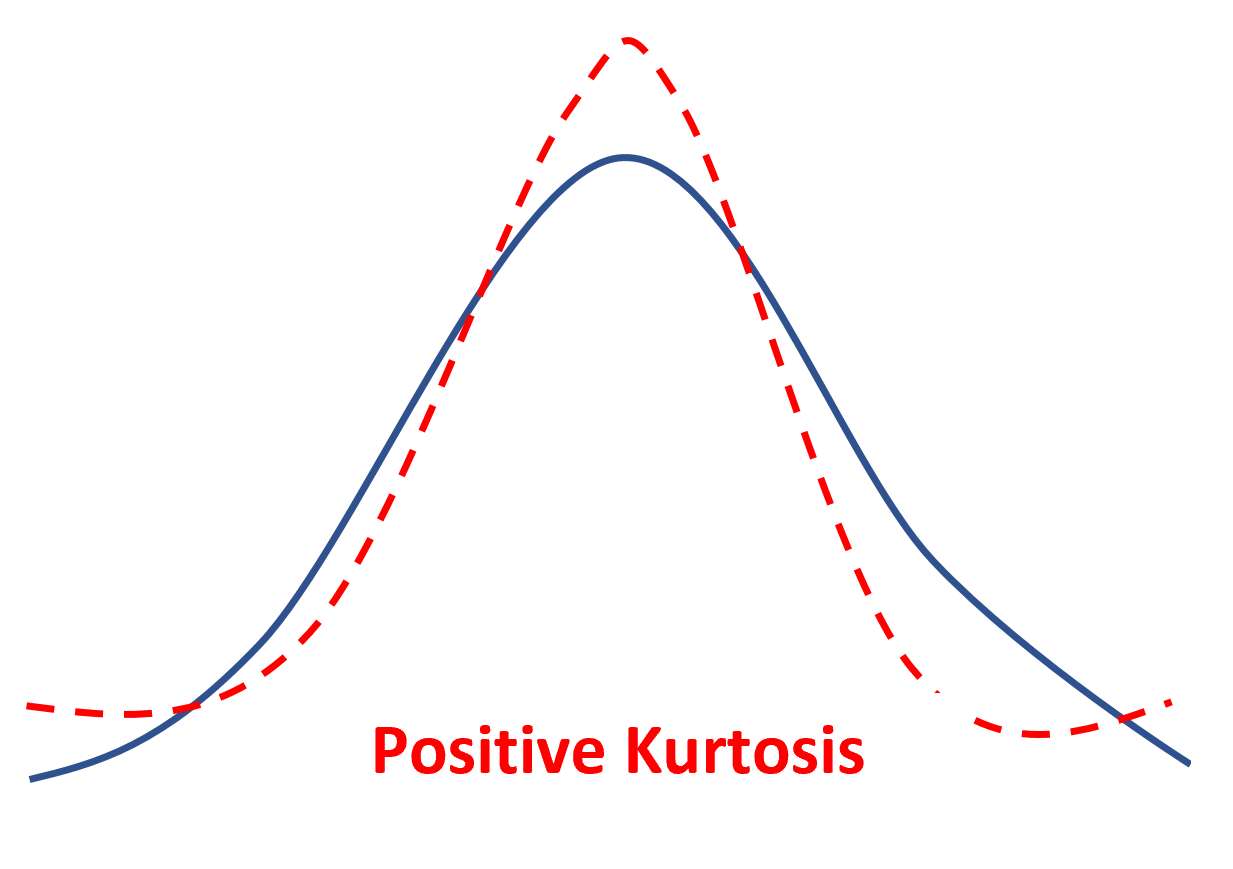
Dit betekent simpelweg dat minder datawaarden zich in de buurt van het gemiddelde bevinden en meer datawaarden aan de staarten.

De meest bekende verdeling met positieve kurtosis is de t-verdeling, die een scherpere piek en zwaardere staarten heeft vergeleken met de normale verdeling.

Negatieve kurtosis

Als een verdeling een negatieve kurtosis heeft, wordt er gesproken van platykurtic , wat betekent dat de verdeling een vlakkere piek en dunnere staarten heeft vergeleken met een normale verdeling.

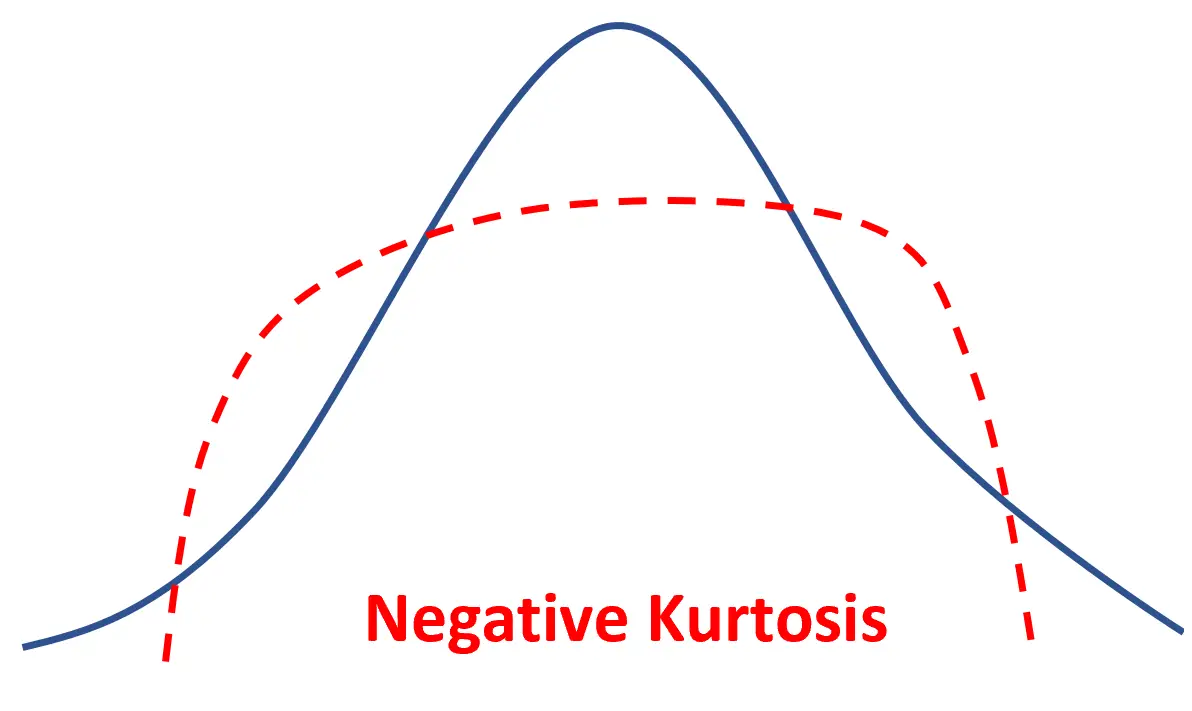
Dit betekent simpelweg dat meer datawaarden zich in de buurt van het gemiddelde bevinden en minder datawaarden aan de staarten.

Een extreem voorbeeld van een verdeling die negatieve kurtosis vertoont, is de uniforme verdeling , die geen pieken kent en een volledig vlakke verdeling is.

Wanneer flatterend gebruiken in de praktijk?

In de praktijk meten we vaak de kurtosis van een verdeling in de verkennende analysefase, wanneer we simpelweg proberen de gegevens beter te begrijpen.

Dus als we zien dat de kurtosis positief is, weten we dat we werken met een distributie met minder datawaarden nabij het midden en meer datawaarden verdeeld langs de staarten.

Omgekeerd, als we zien dat de kurtosis negatief is, weten we dat we werken met een distributie met meer datawaarden nabij het midden en minder datawaarden in de staarten.

Aanvullende bronnen

Om de scheefheid en kurtosis van een bepaalde verdeling te vinden, kunt u de ruwe gegevenswaarden invoeren in deze scheefheids- en kurtosiscalculator , die u zowel de scheefheid als de kurtosis van de verdeling zal vertellen.

Een van de meest populaire statistische tests die worden gebruikt om te bepalen of een bepaalde verdeling al dan niet scheefheid en kurtosis vertoont die overeenkomt met een normale verdeling, is de Jarque Bera-test .

Khan Academy heeft ook een mooie serie video’s waarin wordt beschreven hoe je distributievormen kunt classificeren.