Kendall's tau: definitie + voorbeeld

In de statistiek verwijst correlatie naar de sterkte en richting van een verband tussen twee variabelen. De waarde van een correlatiecoëfficiënt kan variëren van -1 tot 1, waarbij -1 een perfect negatief verband aangeeft, 0 geen verband aangeeft en 1 een perfect positief verband aangeeft.

De meest gebruikte correlatiecoëfficiënt is dePearson-correlatiecoëfficiënt , die de lineaire associatie tussen twee numerieke variabelen meet.

Een minder vaak gebruikte correlatiecoëfficiënt is Kendall’s Tau , die de relatie meet tussen twee kolommen met gerangschikte gegevens.

De formule voor het berekenen van Kendall’s Tau, vaak afgekort τ, is als volgt:

τ = (CD) / (C+D)

Goud:

C = het aantal overeenkomende paren

D = het aantal dissonante paren

Het volgende voorbeeld illustreert hoe u deze formule kunt gebruiken om de rangcorrelatiecoëfficiënt van Kendall’s Tau te berekenen voor twee kolommen met gerangschikte gegevens.

Voorbeeld van het berekenen van Kendall’s Tau

Stel dat twee basketbalcoaches 12 van hun spelers rangschikken van slechtste naar beste. De volgende tabel toont de ranglijst die elke coach aan de spelers heeft toegewezen:

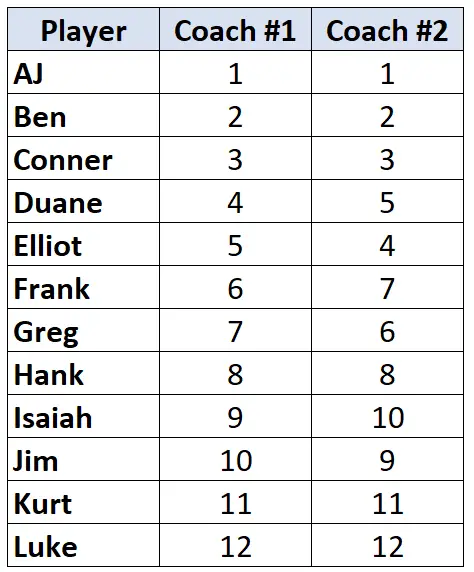
Omdat we met twee kolommen met gerangschikte gegevens werken, is het passend om Kendall’s Tau te gebruiken om de correlatie tussen de rangschikkingen van de twee coaches te berekenen. Volg de volgende stappen om Kendall’s Tau te berekenen:

Stap 1: Tel het aantal overeenkomende paren.

Kijk alleen naar de ranglijst van coach nr. 2. Begin bij de startspeler en tel hoeveel rangen onder hem hoger zijn. Er zijn bijvoorbeeld 11 getallen onder „1“ die groter zijn, dus we schrijven 11:

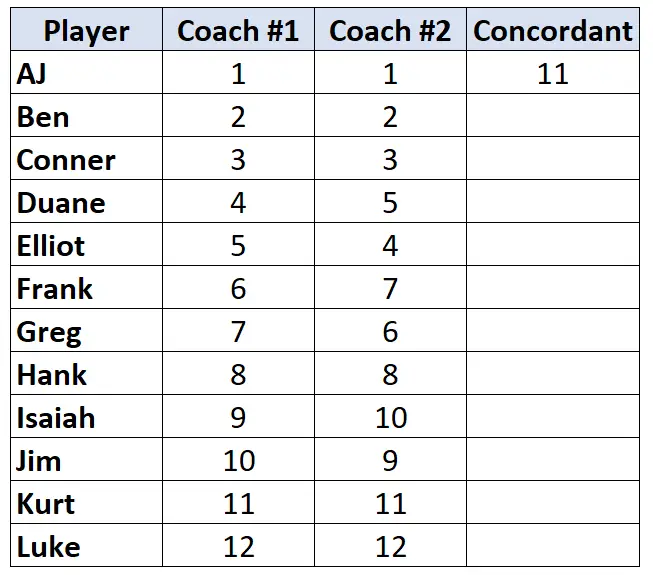
Ga naar de volgende speler en herhaal het proces. Er zijn 10 getallen onder “2” die groter zijn, dus we schrijven er 10:

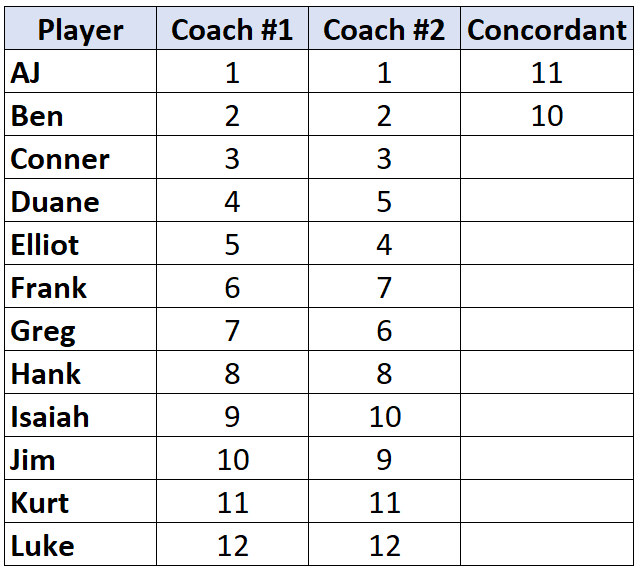
Zodra we een speler bereiken wiens rang lager is dan de speler vóór hem, krijgt hij eenvoudigweg dezelfde waarde toegewezen als de speler vóór hem. Elliot heeft bijvoorbeeld een rang van „4“ die lager is dan de rang van „5“ van de vorige speler, dus hij krijgt eenvoudigweg dezelfde waarde toegewezen als de speler vóór hem:

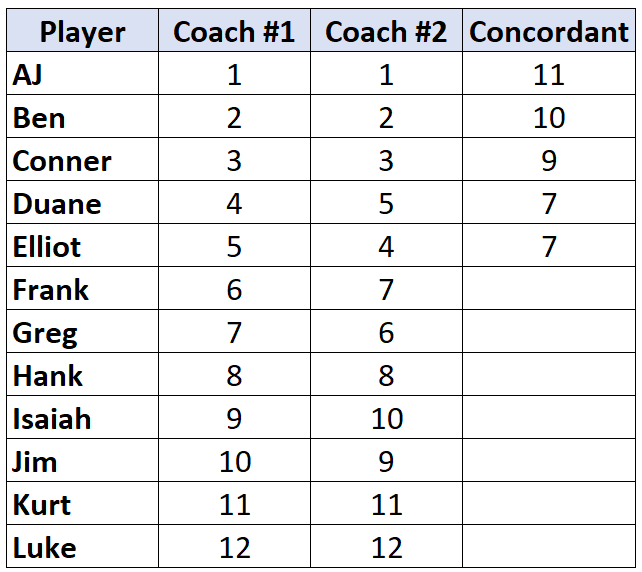
Herhaal dit proces voor alle spelers:

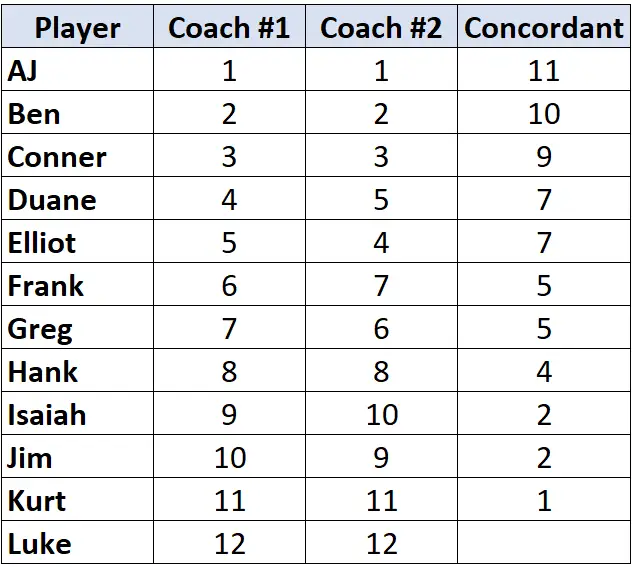
Stap 2: Tel het aantal dissonante paren.

Nogmaals, kijk alleen naar de ranglijst van Coach #2. Tel voor elke speler hoeveel rangen onder hem of haar kleiner zijn. Coach nr. 2 heeft AJ bijvoorbeeld de rang “1” toegewezen en geen enkele speler onder hem heeft een lagere rang. We kennen er dus de waarde 0 aan toe:

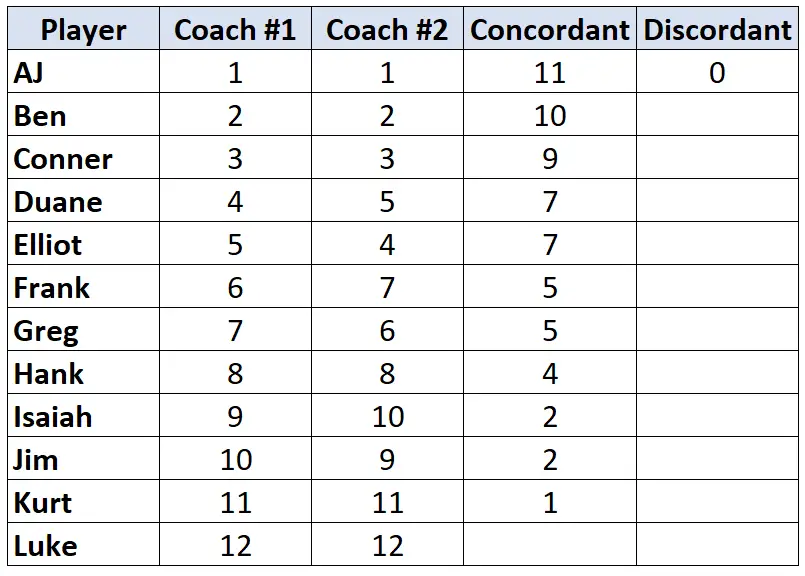
Herhaal dit proces voor elke speler:

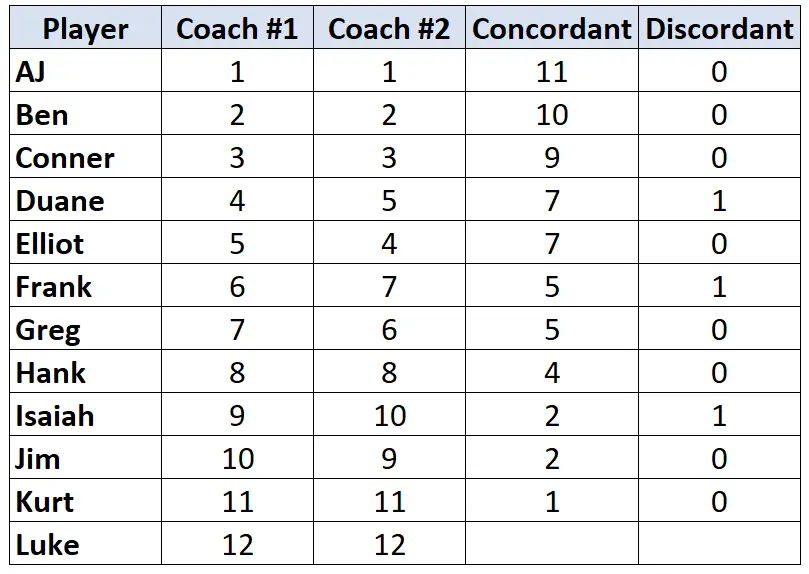
Stap 3: Bereken de som van elke kolom en vind Kendall’s Tau.

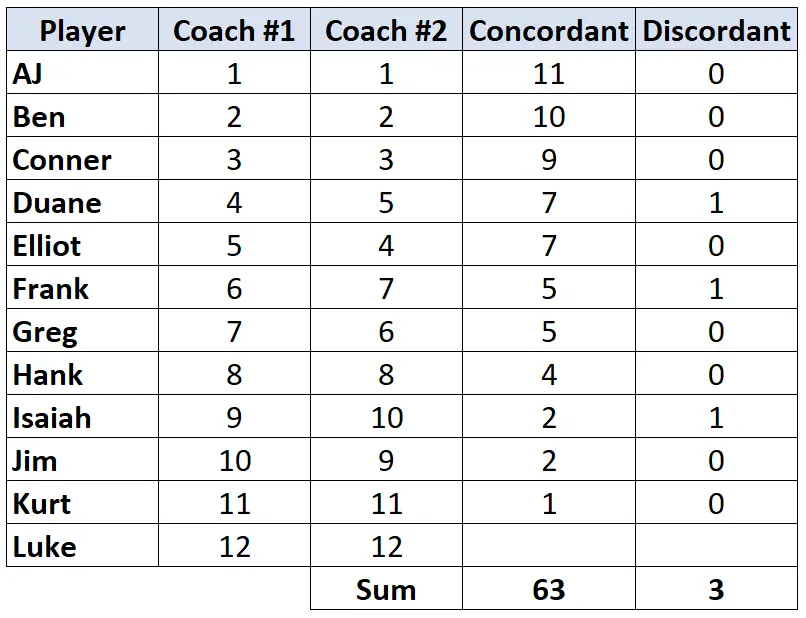
Kendall’s Tau = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Statistisch belang van Kendall’s Tau

Als je meer dan n=10 paren hebt, volgt Kendall’s Tau doorgaans een normale verdeling. U kunt de volgende formule gebruiken om een z-score voor Kendall’s Tau te berekenen:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Goud:

τ = waarde die u hebt berekend voor Kendall’s Tau

n = aantal paren

Zo bereken je z voor het vorige voorbeeld:

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4,11 .

Met behulp van de P-waarde Z-score-calculator zien we dat de p-waarde voor deze z-score 0,00004 is, wat statistisch significant is op het alfaniveau van 0,05. Er is dus een statistisch significante correlatie tussen de rangen die de twee coaches aan de spelers toekenden.

Bonus: Hoe Kendall’s Tau in R te berekenen

In de R-statistieksoftware kunt u de functie kendall.tau() uit de VGAM-bibliotheek gebruiken om de Kendall’s Tau voor twee vectoren te berekenen, waarbij de volgende syntaxis wordt gebruikt:

kendall.tau(x, y)

waarbij x en y twee digitale vectoren van gelijke lengte zijn.

De volgende code illustreert hoe je Kendall’s Tau kunt berekenen voor de exacte gegevens die we in het vorige voorbeeld hebben gebruikt:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Merk op hoe de Tau-waarde van Kendall overeenkomt met de waarde die we handmatig hebben berekend.