Hoe de afstand van cook in python te berekenen

Cook’s afstand wordt gebruikt om invloedrijke observaties in een regressiemodel te identificeren.

De formule voor Cook’s afstand is:

d _ik = ( _ri ² / p*MSE) * (h _ii / (1-h _ii ) ² )

Goud:

• ri is het i _– ^de residu
• p is het aantal coëfficiënten in het regressiemodel
• MSE is de gemiddelde kwadratische fout
• h _ii is de ^i-de hefboomwaarde

In wezen meet de afstand van Cook hoeveel alle aangepaste waarden van het model veranderen wanneer de i ^-de waarneming wordt verwijderd.

Hoe groter de waarde van Cooks afstand, hoe invloedrijker een bepaalde waarneming is.

Als algemene regel wordt aangenomen dat elke waarneming met een Cook’s afstand groter dan 4/n (waarbij n = totaal aantal waarnemingen) een grote invloed heeft.

Deze tutorial biedt een stapsgewijs voorbeeld van hoe je de afstand van Cook kunt berekenen voor een bepaald regressiemodel in Python.

Stap 1: Voer de gegevens in

Eerst maken we een kleine dataset om mee te werken in Python:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' x ': [8, 12, 12, 13, 14, 16, 17, 22, 24, 26, 29, 30],
                   ' y ': [41, 42, 39, 37, 35, 39, 45, 46, 39, 49, 55, 57]})

Stap 2: Pas het regressiemodel aan

Vervolgens passen we een eenvoudig lineair regressiemodel toe:

 import statsmodels. api as sm

#define response variable
y = df[' y ']

#define explanatory variable
x = df[' x ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

Stap 3: Bereken de kookafstand

Vervolgens berekenen we de Cook-afstand voor elke waarneming in het model:

 #suppress scientific notation
import numpy as np
n.p. set_printoptions (suppress= True )

#create instance of influence
influence = model. get_influence ()

#obtain Cook's distance for each observation
cooks = influence. cooks_distance

#display Cook's distances
print (cooks)

(array([0.368, 0.061, 0.001, 0.028, 0.105, 0.022, 0.017, 0. , 0.343,
        0. , 0.15 , 0.349]),
 array([0.701, 0.941, 0.999, 0.973, 0.901, 0.979, 0.983, 1. , 0.718,
        1. , 0.863, 0.713]))

Standaard geeft de functie cooks_distance() voor elke waarneming een reeks waarden weer voor de afstand van Cook, gevolgd door een reeks overeenkomstige p-waarden.

Bijvoorbeeld:

• Cook’s afstand voor observatie #1: 0,368 (p-waarde: 0,701)
• Cook’s afstand voor observatie #2: 0,061 (p-waarde: 0,941)
• Cook’s afstand voor observatie #3: 0,001 (p-waarde: 0,999)

Enzovoort.

Stap 4: Visualiseer de afstanden van de kok

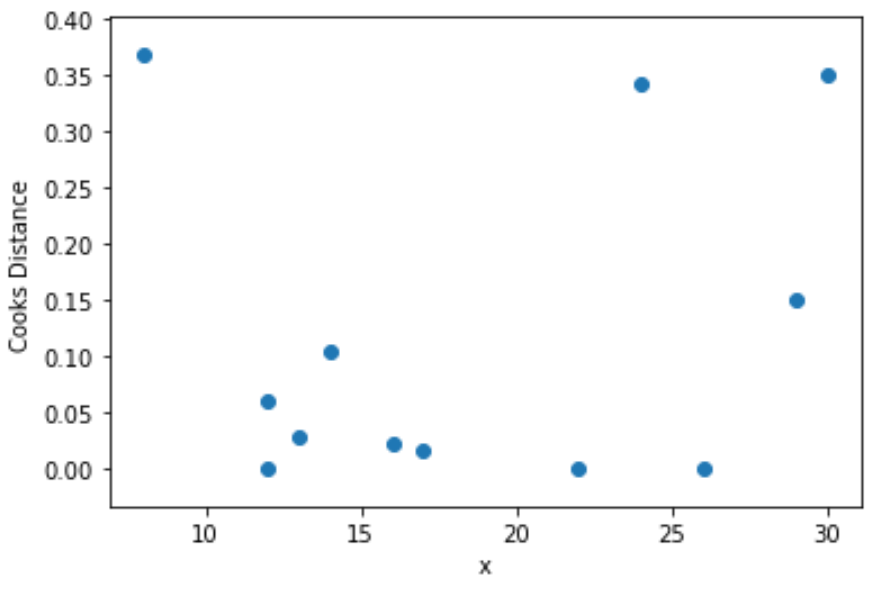
Ten slotte kunnen we een spreidingsdiagram maken om de waarden van de voorspellende variabele te visualiseren als functie van de afstand van Cook voor elke waarneming:

 import matplotlib. pyplot as plt

plt. scatter (df.x, cooks[0])
plt. xlabel (' x ')
plt. ylabel (' Cooks Distance ')
plt. show () 

Laatste gedachten

Het is belangrijk op te merken dat de afstand van Cook moet worden gebruikt om potentieel invloedrijke waarnemingen te identificeren . Het feit dat een waarneming invloedrijk is, betekent niet dat deze uit de dataset moet worden verwijderd.

Eerst moet u verifiëren dat de waarneming niet het gevolg is van een gegevensinvoerfout of een andere vreemde gebeurtenis. Als het een legitieme waarde blijkt te zijn, kunt u beslissen of het gepast is om deze te verwijderen, te laten zoals hij is, of eenvoudigweg te vervangen door een alternatieve waarde zoals de mediaan.