Lagere vierkanten

Von Dr.benjamin anderson August 2, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de kleinste kwadratenmethode is in de statistiek, wat de kleinste kwadratenmethode is en hoe een regressiemodel wordt aangepast aan het kleinste kwadratencriterium.

Wat is de kleinste kwadratenmethode?

De kleinste kwadratenmethode is een statistische methode die wordt gebruikt om de vergelijking van een regressie te bepalen. Met andere woorden: de kleinste kwadratenmethode is een criterium dat in een regressiemodel wordt gebruikt om de fout die wordt verkregen bij het berekenen van de regressievergelijking te minimaliseren.

Concreet bestaat de kleinste-kwadratenmethode uit het minimaliseren van de som van de kwadraten van de residuen, of met andere woorden, het is gebaseerd op het minimaliseren van de som van de kwadraten van de verschillen tussen de waarden voorspeld door het regressiemodel en de waargenomen waarden. . . Hieronder zullen we in detail zien hoe een regressiemodel wordt gefit op basis van het kleinste kwadratencriterium.

Het belangrijkste kenmerk van de kleinste kwadratenmethode is dat de langste afstanden tussen de waargenomen waarden en de regressiefunctie worden geminimaliseerd. In tegenstelling tot andere regressiecriteria vindt de kleinste kwadratenmethode het belangrijker om grote residuen te minimaliseren dan kleine residuen, aangezien het kwadraat van een groot getal veel groter is dan het kwadraat van een klein getal. nummer.

Schattingsfout

Om het concept van de kleinste kwadraten volledig te begrijpen, moeten we eerst duidelijk zijn over wat residuen zijn in een regressiemodel. We zullen hieronder daarom zien wat een schattingsfout is en hoe deze wordt berekend.

In de statistiek is de schattingsfout , ook wel residueel genoemd, het verschil tussen de werkelijke waarde en de waarde die door het regressiemodel wordt aangepast. Een statistisch residu wordt daarom als volgt berekend:

$e_i=y_i-\widehat{y}_i$

Goud:

$e_i$

is het residu van gegevens i.
$y_i$

is de echte waarde van gegevens i.
$\widehat{y}_i$

is de waarde die wordt geleverd door het regressiemodel voor gegevens i.

Dus hoe groter het residu van een stukje data, hoe slechter het regressiemodel is aangepast aan dit stukje data. Dus hoe kleiner een residu, hoe kleiner de afstand tussen de werkelijke waarde en de voorspelde waarde.

Op dezelfde manier betekent het dat als het residu van een stuk gegevens positief is, het regressiemodel een waarde voorspelt die lager is dan de werkelijke waarde. terwijl als het residu negatief is, dit betekent dat de voorspelde waarde groter is dan de werkelijke waarde.

Minimaliseer foutvierkanten

Nu we weten wat een residu in de statistiek is, zal het gemakkelijker zijn om te begrijpen hoe foutvierkanten worden geminimaliseerd.

Het kwadraat van een fout is het kwadraat van een residu, dus het kwadraat van een fout is gelijk aan het verschil tussen de werkelijke waarde en de waarde die wordt aangepast door het regressiemodel, verheven tot de macht twee.

$e_i^2=(y_i-\widehat{y}_i)^2$

Goud:

$e_i^2$

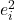
is het kwadraat van de rest van gegevens i.
$y_i$

is de echte waarde van gegevens i.
$\widehat{y}_i$

is de waarde die wordt geleverd door het regressiemodel voor gegevens i.

De kleinste kwadratenmethode bestaat dus uit het creëren van een regressiemodel door de som van de kwadraten van de fouten te minimaliseren . Het kleinste kwadratencriterium is daarom gebaseerd op de minimalisatie van de volgende uitdrukking:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

Daarom wordt het kleinste kwadratencriterium ook wel het kleinste kwadratencriterium genoemd.

Zoals je in de vorige formule kunt zien, hecht het kleinste kwadratencriterium meer belang aan het minimaliseren van grote residuen dan aan kleine residuen. Als één residu bijvoorbeeld 3 is en een ander residu 5, zijn hun vierkanten respectievelijk 9 en 25, dus het kleinste kwadratencriterium zal prioriteit geven aan het minimaliseren van het tweede residu vóór het eerste residu.

Kleinste kwadraten aanpassing

Het passen van een regressiemodel met behulp van het kleinste kwadratencriterium bestaat uit het vinden van een regressiemodel dat de kwadraten van de residuen minimaliseert. Daarom zal de uit het regressiemodel verkregen vergelijking er een zijn waarvan de kwadraten van de verschillen tussen de waargenomen waarden en de aangepaste waarden minimaal zijn.

Merk op dat er in het volgende voorbeeld meer criteria zijn voor het maken van een regressiemodel en dat, afhankelijk van het gekozen criterium, de regressievergelijking anders is.

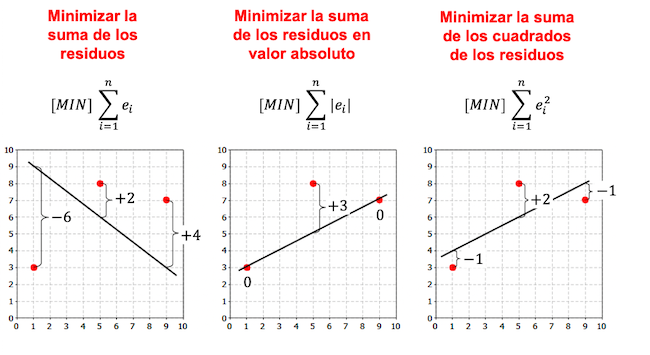
kleinste kwadratenmethode, kleinste kwadratenaanpassing

Zoals u in de voorgaande voorbeelden kunt zien, hangt de lijn die wordt verkregen uit het lineaire regressiemodel voor dezelfde gegevensset af van het gekozen criterium. Over het algemeen wordt in regressiemodellen het kleinste kwadratencriterium gebruikt.

In de statistiek is het meest gebruikte regressiemodel het eenvoudige lineaire regressiemodel, dat bestaat uit het benaderen van de relatie tussen de onafhankelijke variabele X en de afhankelijke variabele Y met behulp van een rechte lijn.

$y=b_0+b_1x$

De formules voor het aanpassen van een dataset aan een eenvoudig lineair regressiemodel zijn dus:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

U kunt een voorbeeld zien van hoe een eenvoudig lineair regressiemodel wordt berekend met behulp van het kleinste kwadratencriterium door op de volgende link te klikken:

➤ Zie: Voorbeeld van eenvoudige lineaire regressie

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder