Hoe de kleinste kwadratenmethode in r te gebruiken

De kleinste kwadratenmethode is een methode die we kunnen gebruiken om de regressielijn te vinden die het beste bij een gegeven set gegevens past.

Om de kleinste kwadratenmethode te gebruiken om een regressielijn in R te passen, kunnen we de functie lm() gebruiken.

Deze functie gebruikt de volgende basissyntaxis:

 model <- lm(response ~ predictor, data=df)

Het volgende voorbeeld laat zien hoe u deze functie in R kunt gebruiken.

Voorbeeld: kleinste kwadratenmethode in R

Stel dat we het volgende gegevensframe in R hebben dat het aantal gestudeerde uren en de bijbehorende examenscore voor 15 studenten in een klas weergeeft:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

We kunnen de functie lm() gebruiken om de kleinste kwadratenmethode te gebruiken om een regressielijn aan deze gegevens te koppelen:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Uit de waarden in de kolom Geschat resultaat kunnen we de volgende aangepaste regressielijn schrijven:

Examenscore = 65.334 + 1.982 (uren)

Zo interpreteert u elke coëfficiënt in het model:

• Intercept : Voor een student die 0 uur studeert, is de verwachte examenscore 65.334 .
• uren : Voor elk bijkomend uur dat gestudeerd wordt, stijgt de verwachte examenscore met 1.982 .

We kunnen deze vergelijking gebruiken om een schatting te maken van het examencijfer dat een student zal ontvangen op basis van de bestudeerde uren.

Als een student bijvoorbeeld 5 uur studeert, schatten we dat zijn examenscore 75,244 zou zijn:

Examenscore = 65.334 + 1.982(5) = 75.244

Ten slotte kunnen we een spreidingsdiagram maken van de originele gegevens met de passende regressielijn over de grafiek heen:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

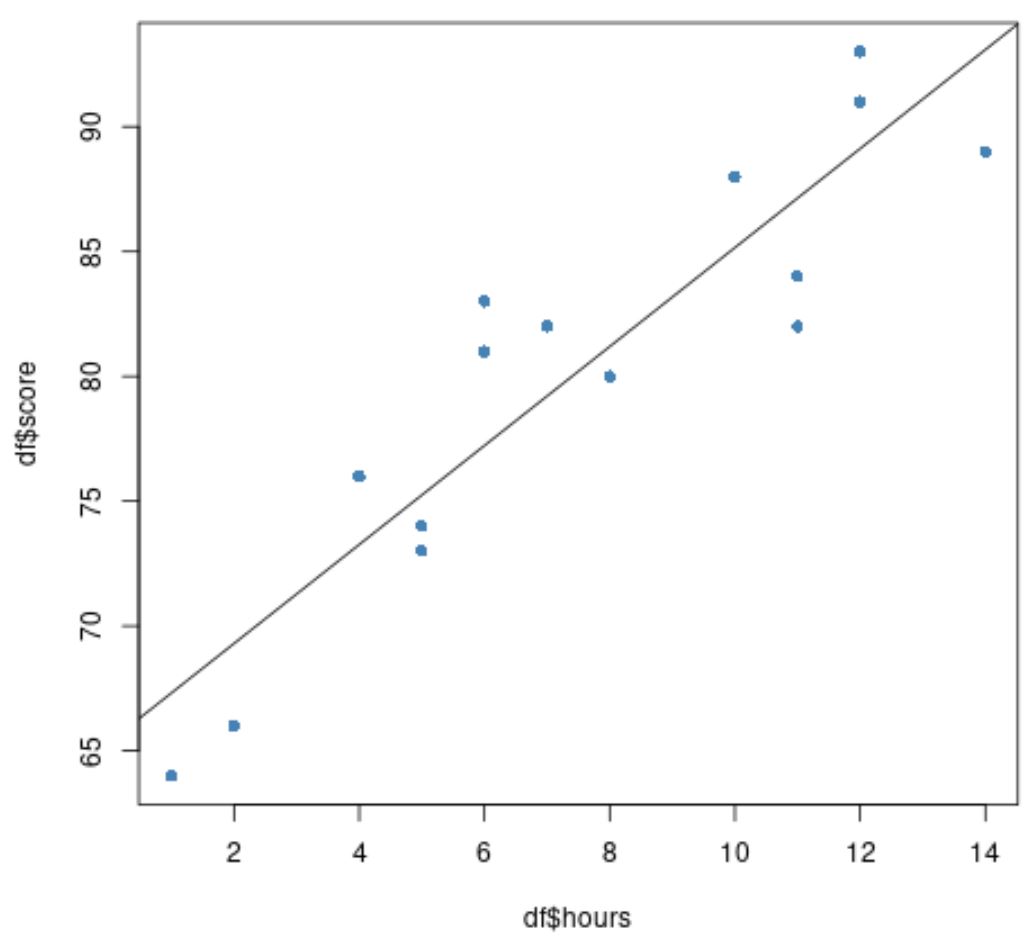
De blauwe cirkels vertegenwoordigen de gegevens en de zwarte lijn vertegenwoordigt de gepaste regressielijn.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe maak je een restplot in R
Hoe te testen op multicollineariteit in R
Hoe u curve-fitting uitvoert in R