Hoe de kookafstand in sas te berekenen

Cook’s afstand wordt gebruikt om invloedrijke observaties in een regressiemodel te identificeren.

De formule voor Cook’s afstand is:

d _ik = ( _ri ² / p*MSE) * (h _ii / (1-h _ii ) ² )

Goud:

• ri is het i _– ^de residu
• p is het aantal coëfficiënten in het regressiemodel
• MSE is de gemiddelde kwadratische fout
• h _ii is de ^i-de hefboomwaarde

In wezen meet de afstand van Cook hoeveel alle aangepaste waarden van het model veranderen wanneer de i ^-de waarneming wordt verwijderd.

Hoe groter de waarde van Cooks afstand, hoe invloedrijker een bepaalde waarneming is.

Over het algemeen wordt aangenomen dat elke waarneming met een Cook-afstand groter dan 4/n (waarbij n = totaal aantal waarnemingen) een grote invloed heeft.

In het volgende voorbeeld ziet u hoe u de afstand van Cook voor elke waarneming in een regressiemodel in SAS kunt berekenen.

Voorbeeld: Berekening van de afstand van de kok in SAS

Laten we aannemen dat we de volgende gegevensset in SAS hebben:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

We kunnen PROC REG gebruiken om een eenvoudig lineair regressiemodel aan deze dataset te koppelen en vervolgens de OUTPUT- instructie met de COOKD- instructie gebruiken om de Cook’s afstand voor elke waarneming in het regressiemodel te berekenen:

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

De tabel met uiteindelijke resultaten toont de originele dataset samen met de Cook-afstand voor elke waarneming:

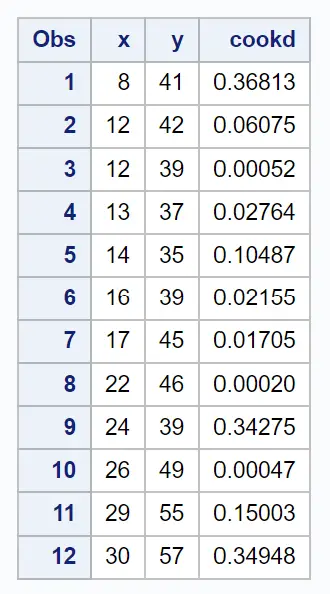
We kunnen bijvoorbeeld zien:

• De Cook-afstand voor de eerste waarneming is 0,36813 .
• De Cook-afstand voor de tweede waarneming is 0,06075 .
• De Cook-afstand voor de derde waarneming is 0,00052 .

Enzovoort.

De PROC REG- procedure produceert ook verschillende diagnostische grafieken in de uitvoer en de Cook Distance-grafiek is te zien in deze uitvoer:

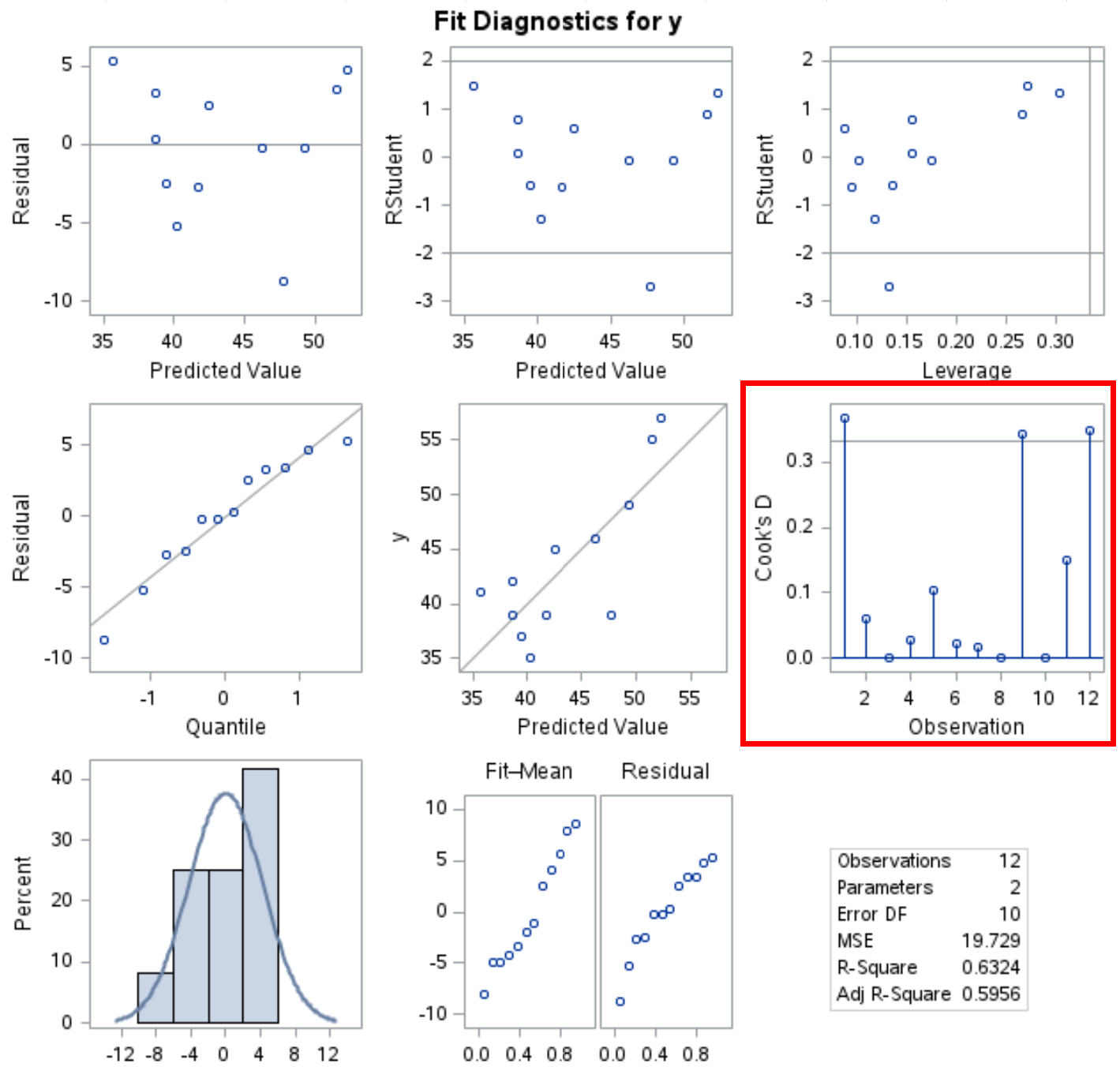
Op de x-as wordt het observatienummer weergegeven en op de y-as de Cook-afstand voor elke observatie.

Merk op dat er een grenslijn is geplaatst op 4/n (in dit geval n = 12, dus de grens ligt op 0,33) en we kunnen zien dat drie waarnemingen in de dataset groter zijn dan deze lijn.

Dit geeft aan dat deze waarnemingen een grote invloed kunnen hebben op het regressiemodel en misschien nader moeten worden onderzocht voordat de modelresultaten worden geïnterpreteerd.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u een restplot maakt in SAS
Histogrammen maken in SAS
Hoe puntenwolken te creëren in SAS
Hoe uitschieters in SAS te identificeren