Hoe u een kpss-test uitvoert in python

Om te bepalen of een tijdreeks een stationaire trend heeft, kan een KPSS-test worden gebruikt.

Deze test maakt gebruik van de volgende nul- en alternatieve hypothese:

• H ₀ : De tijdreeks heeft een stationaire trend.
• H _A : De tijdreeks kent geen stationaire trend.

Als de p-waarde van de test onder een bepaald significantieniveau ligt (bijvoorbeeld α = 0,05), dan verwerpen we de nulhypothese en concluderen we dat de tijdreeks geen stationaire trend kent.

Anders zullen we er niet in slagen de nulhypothese te verwerpen.

De volgende voorbeelden laten zien hoe u een KPSS-test in Python uitvoert.

Voorbeeld 1: KPSS-test in Python (met stationaire data)

Laten we eerst een aantal nepgegevens in Python maken om mee te werken:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seed ( 1 )

#create time series data
data = np. random . normal (size= 100 )

#create line plot of time series data
plt. plot (data) 

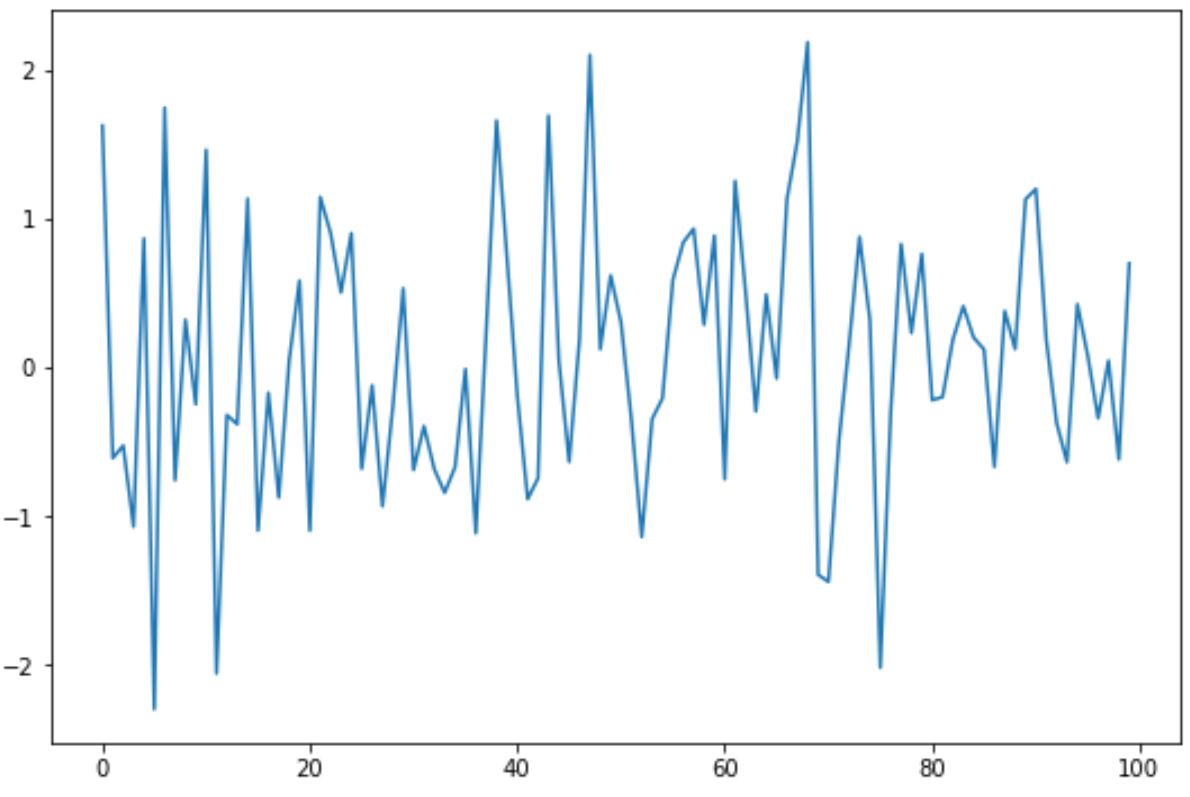
We kunnen de functie kpss() uit het statsmodels- pakket gebruiken om een KPSS-test uit te voeren op deze tijdreeksgegevens:

 import statsmodels. api as sm

#perform KPSS test
sm. tsa . stattools . kpss (data, regression=' ct ')

(0.0477617848370993,
 0.1,
 1,
 {'10%': 0.119, '5%': 0.146, '2.5%': 0.176, '1%': 0.216})

InterpolationWarning: The test statistic is outside of the range of p-values available
in the look-up table. The actual p-value is greater than the p-value returned.

Zo interpreteert u het resultaat:

• De KPSS-teststatistiek: 0,04776
• De p-waarde: 0,1
• De parameter voor de truncatie-offset: 1
• Kritische waarden bij 10% , 5% , 2,5% en 1%

De p-waarde is 0,1 . Omdat deze waarde niet minder dan 0,05 bedraagt, slagen we er niet in de nulhypothese van de KPSS-test te verwerpen.

Dit betekent dat we kunnen aannemen dat de tijdreeks een stationaire trend kent.

Opmerking 1 : De p-waarde is feitelijk nog steeds groter dan 0,1, maar de laagste waarde die de functie kpss() zal produceren is 0,1.

Opmerking 2 : U moet het argument regressie=’ct‘ gebruiken om aan te geven dat de nulhypothese van de test is dat de gegevens een stationaire trend vertonen.

Voorbeeld 2: KPSS-test in Python (met niet-stationaire data)

Laten we eerst een aantal nepgegevens in Python maken om mee te werken:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seed ( 1 )

#create time series data
data =np. array ([0, 3, 4, 3, 6, 7, 5, 8, 15, 13, 19, 12, 29, 15, 45, 23, 67, 45])

#create line plot of time series data
plt. plot (data) 

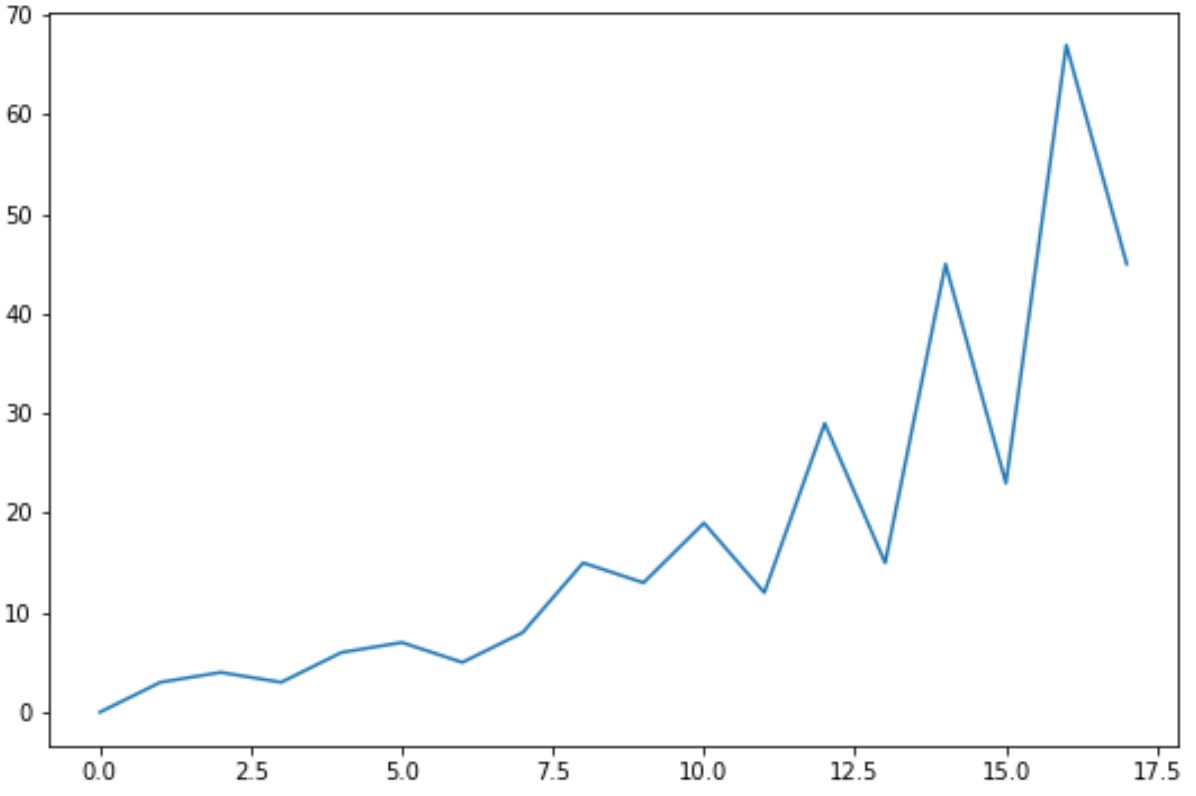
Opnieuw kunnen we de functie kpss() uit het statsmodels- pakket gebruiken om een KPSS-test uit te voeren op deze tijdreeksgegevens:

 import statsmodels. api as sm

#perform KPSS test
sm. tsa . stattools . kpss (data, regression=' ct ')

(0.15096358910843685,
 0.04586367574296928,
 3,
 {'10%': 0.119, '5%': 0.146, '2.5%': 0.176, '1%': 0.216})

Zo interpreteert u het resultaat:

• De KPSS-teststatistiek: 0,1509
• De p-waarde: 0,0458
• De parameter voor de truncatie-offset: 3
• Kritische waarden bij 10% , 5% , 2,5% en 1%

De p-waarde is 0,0458 . Omdat deze waarde kleiner is dan 0,05, verwerpen we de nulhypothese van de KPSS-test.

Dit betekent dat de tijdreeks niet stationair is .

Opmerking : u kunt hier de volledige documentatie voor de functie kpss() van het statsmodels-pakket vinden.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over het werken met tijdreeksgegevens in Python:

Hoe u een uitgebreide Dickey-Fuller-test uitvoert in Python
Hoe u een Mann-Kendall-trendtest uitvoert in Python
Hoe een tijdreeks in Matplotlib te plotten