Kritische waarde

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de kritische waarde is in de statistiek en hoe deze moet worden geïnterpreteerd bij het testen van hypothesen. Op dezelfde manier kunt u zien hoe de kritische waarde wordt berekend, evenals verschillende concrete voorbeelden.

Wat is kritische waarde?

De kritische waarde is het punt in de verdeling van de teststatistiek dat het gebied van verwerping van de nulhypothese scheidt van het gebied van aanvaarding. Met andere woorden, de kritische waarde is de waarde van de verdeling van de statistische test die de grens van het afwijzingsgebied (of kritische gebied) markeert.

Normaal gesproken wordt de kritische waarde weergegeven door het symbool Z _α/2 , aangezien de meest voorkomende referentieverdeling doorgaans de standaardnormale verdeling is.

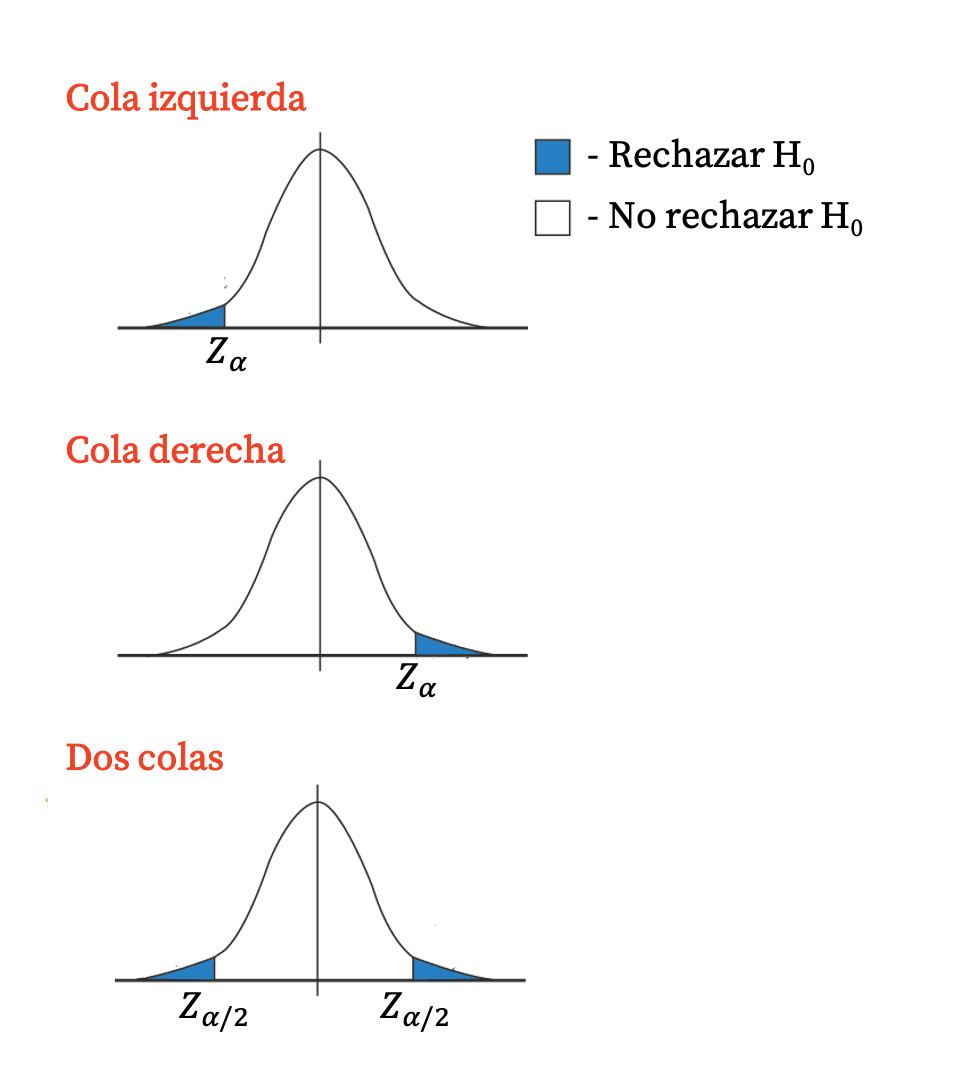
Over het algemeen zijn eenzijdige tests van cruciaal belang, omdat het afwijzingsgebied één staart van de verdeling vormt. Aan de andere kant hebben tweezijdige tests twee kritische waarden, omdat het afstotingsgebied overeenkomt met beide staarten van de verdeling.

Bij betrouwbaarheidsintervallen zijn kritische waarden de punten in de referentieverdeling die de grenzen van het betrouwbaarheidsinterval markeren.

Hoe de kritische waarde te berekenen

We zullen dan zien hoe de meest voorkomende kritische waarden worden berekend. De kritische waarde van Z en de kritische waarde van t worden berekend voor het betrouwbaarheidsinterval van het gemiddelde. Het enige verschil is dat de kritische waarde van Z wordt berekend wanneer de standaarddeviatie van de populatie bekend is, en in plaats daarvan wordt de kritische waarde van t gebruikt. wanneer slechts de gegevens van één monster bekend zijn.

Kritische waarde van Z

De kritische waarde van Z wordt gebruikt om de grenzen van het betrouwbaarheidsinterval voor het gemiddelde te bepalen. Om precies te zijn: het wordt alleen gebruikt als u de standaarddeviatie van de populatie kent.

Om de kritische waarde van Z te berekenen, moet de waarde die overeenkomt met de waarschijnlijkheid van de helft van het significantieniveau worden gevonden in de standaardnormale verdelingstabel .

Als we bijvoorbeeld een betrouwbaarheidsinterval voor het gemiddelde willen bepalen met een betrouwbaarheidsniveau van 95%, betekent dit dat het significantieniveau 5% is. Daarom is het noodzakelijk om in de tabel met de standaardnormale verdeling te zien welke waarde overeenkomt met een waarschijnlijkheid van 2,5%, aangezien het betrouwbaarheidsinterval voor het gemiddelde tweezijdig is.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Hieronder zie je een tabel met de meest gebruikte kritische Z-waarden:

Betrouwbaarheidsniveau (1-α)	Betekenisniveau (α)	Kritische waarde (Z _α/2 )
0,80	0,20	1.282
0,85	0,15	1.440
0,90	0,10	1.645
0,95	0,05	1960
0,99	0,01	2.576
0,995	0,005	2.807
0,999	0,001	3.291

Kritische waarde van t

De kritische t-waarde wordt gebruikt om de grenzen van het betrouwbaarheidsinterval voor het gemiddelde te vinden wanneer de standaarddeviatie van de populatie onbekend is.

Om de kritische waarde van t te berekenen, moet de waarde die overeenkomt met de waarschijnlijkheid van de helft van het significantieniveau worden gevonden in de Student’s t-verdelingstabel , waarbij er rekening mee moet worden gehouden dat de vrijheidsgraden van de Student’s t-verdeling een eenheid zijn. dan de steekproefomvang.

Als we bijvoorbeeld het betrouwbaarheidsinterval willen vinden met een betrouwbaarheidsniveau van 95% en de steekproefomvang 8 is, moeten we toegang krijgen tot de Student’s t-verdelingstabel en zien welke waarde overeenkomt met t _0.025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Zie: Het betrouwbaarheidsinterval van het gemiddelde berekenen

De kritische waarde bij het testen van hypothesen

De kritische waarde kan ook worden gebruikt bij het testen van hypothesen om de nulhypothese te verwerpen (en de alternatieve hypothese te accepteren) of de alternatieve hypothese te verwerpen (en de nulhypothese te accepteren).

Als de waarde van de verdeling van de teststatistiek die overeenkomt met de p-waarde binnen het interval ligt dat wordt gemarkeerd door de kritische waarden, wordt de nulhypothese niet verworpen (de alternatieve hypothese wordt verworpen).
Als de waarde van de verdeling van de teststatistiek die overeenkomt met de p-waarde buiten het interval ligt dat wordt gemarkeerd door de kritische waarden, wordt de nulhypothese verworpen (de alternatieve hypothese wordt geaccepteerd).

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder