Wat is kromlijnige regressie? (definitie & voorbeelden)
Curvilineaire regressie is de naam die wordt gegeven aan elk regressiemodel dat probeert in een curve te passen in plaats van in een rechte lijn.
Veel voorkomende voorbeelden van kromlijnige regressiemodellen zijn onder meer:
Kwadratische regressie: gebruikt wanneer er een kwadratische relatie bestaat tussen een voorspellende variabele en eenresponsvariabele . In een grafiek ziet dit type relatie eruit als een „U“ of een omgekeerde „U“ in een spreidingsdiagram:
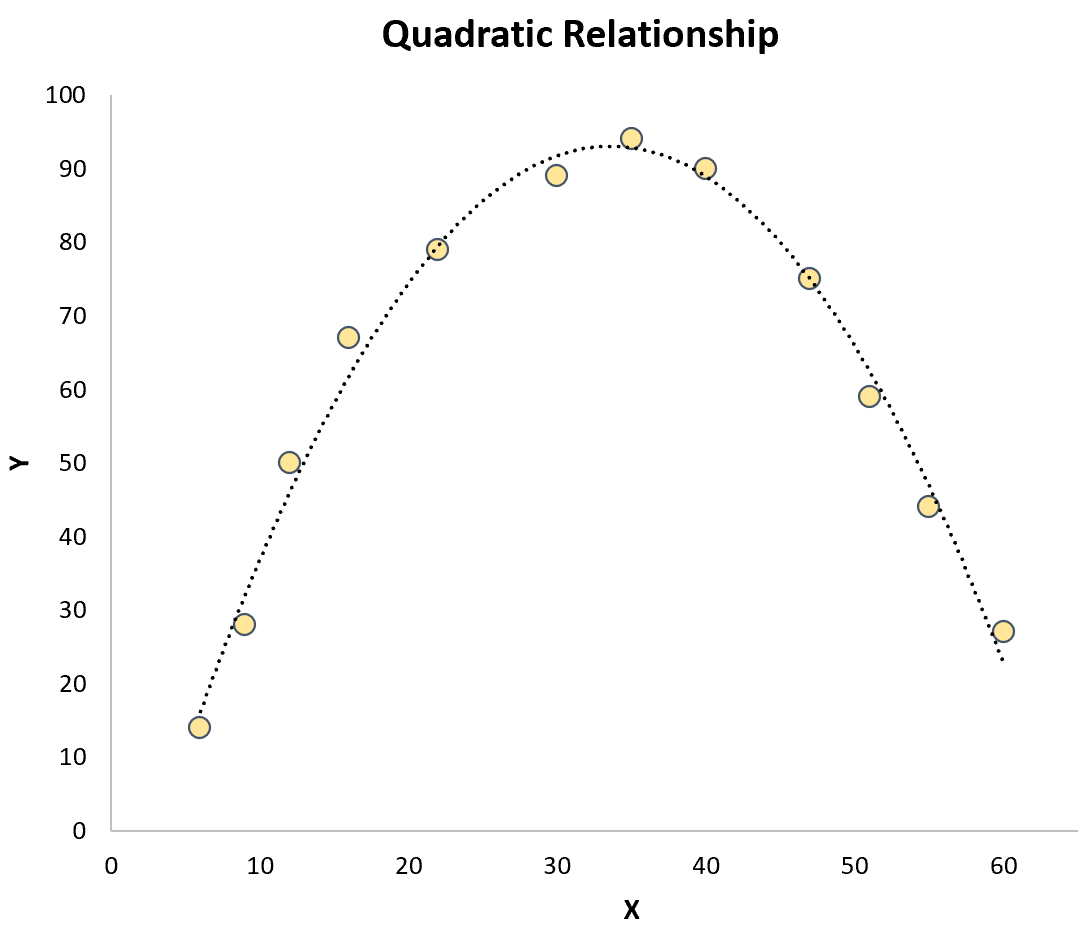
Kubieke regressie: wordt gebruikt wanneer er een kubieke relatie bestaat tussen een voorspellende variabele en een responsvariabele. Wanneer dit type relatie grafisch wordt weergegeven, vertoont het twee verschillende curven op een spreidingsdiagram:
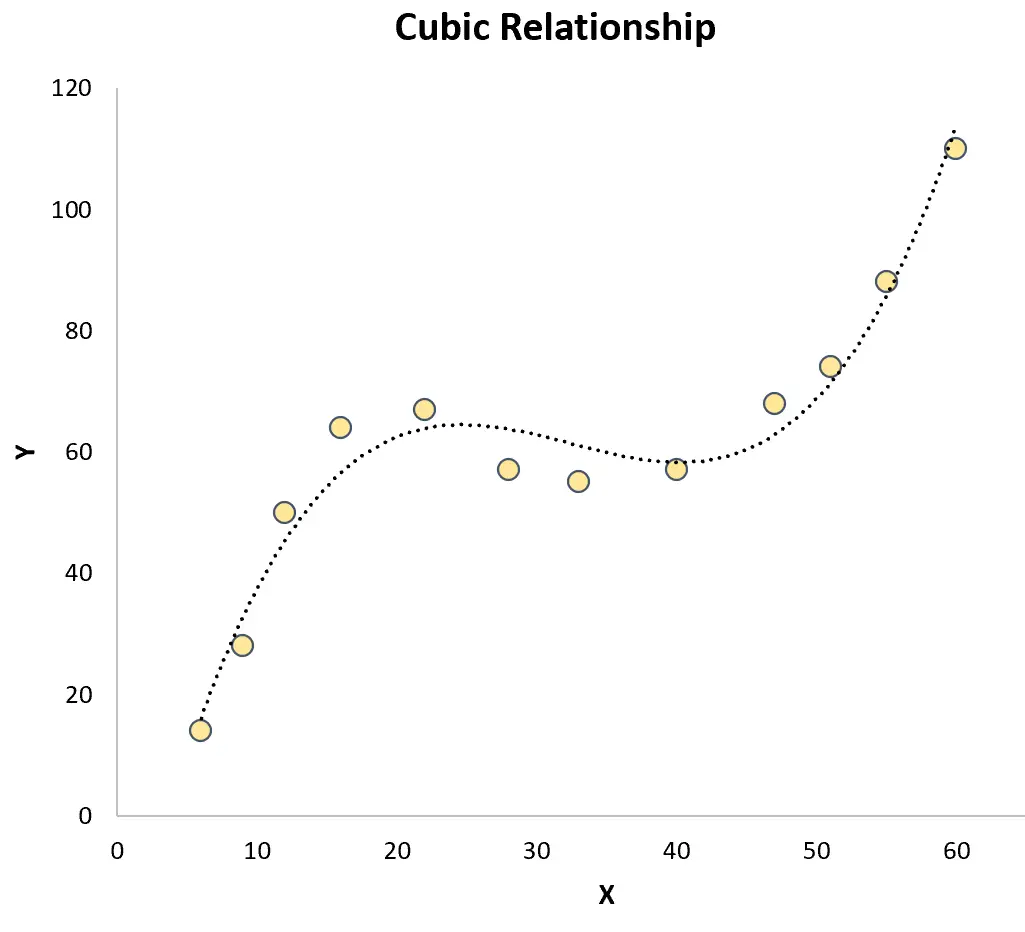
Beide staan in contrast met eenvoudige lineaire regressie waarbij de relatie tussen de voorspellende variabele en de responsvariabele lineair is:
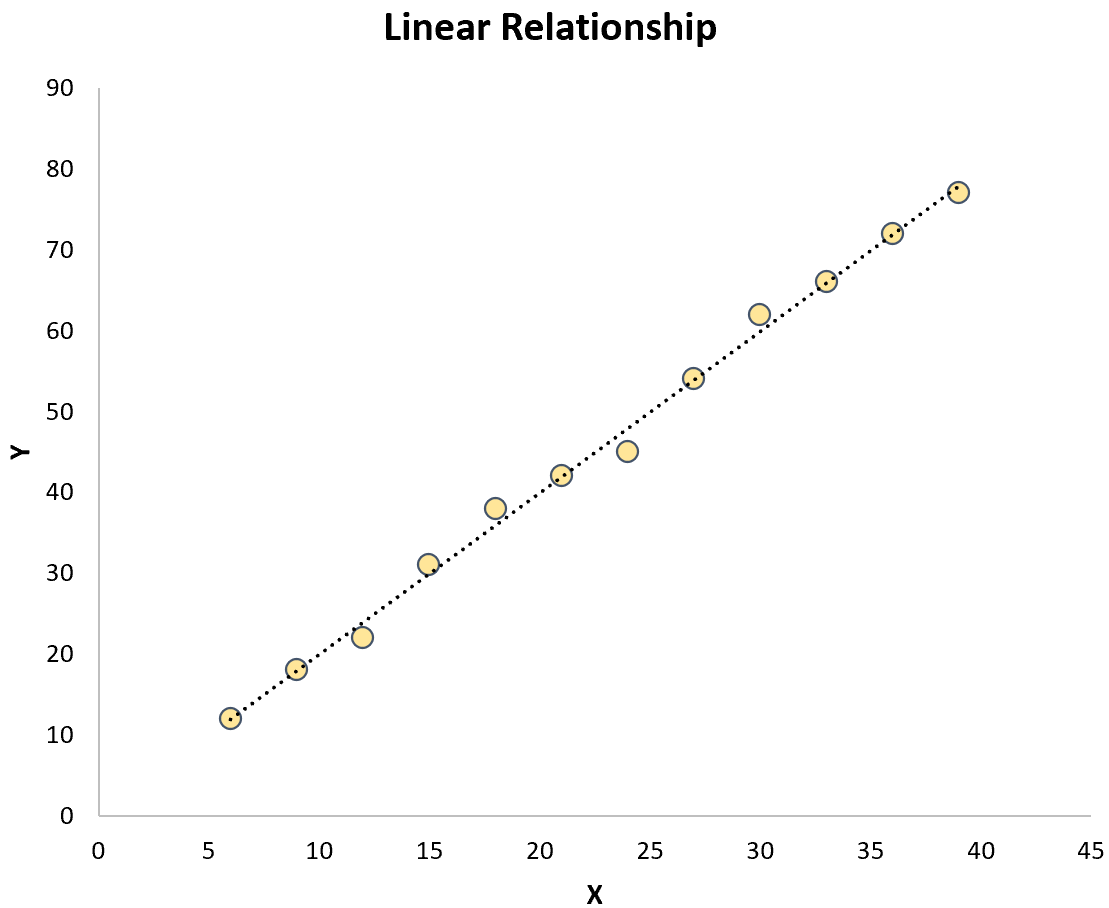
De formule voor kromlijnige regressiemodellen
Een eenvoudig lineair regressiemodel probeert een reeks gegevens te passen met behulp van de volgende formule:
ŷ = β 0 + β 1 x
Goud:
- ŷ: De responsvariabele
- β 0 , β 1 : De regressiecoëfficiënten
- x: de voorspellende variabele
Een kwadratisch regressiemodel gebruikt daarentegen de volgende formule:
ŷ = β 0 + β 1 x + β 2 x 2
En een kubisch regressiemodel gebruikt de volgende formule:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Een meer algemene naam die wordt gegeven aan regressiemodellen die exponenten bevatten, is polynomiale regressie , waarvoor de volgende formule nodig is:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
De waarde van k geeft de graad van de polynoom aan. Hoewel de graad elk positief getal kan zijn, passen we in de praktijk zelden polynomiale regressiemodellen toe met een graad groter dan 3 of 4.
Door exponenten te gebruiken in de formule van het regressiemodel, kunnen polynomiale regressiemodellen curven in datasets passen in plaats van rechte lijnen.
Wanneer kromlijnige regressie gebruiken?
De eenvoudigste manier om te weten of u wel of niet kromlijnige regressie moet gebruiken, is door een spreidingsdiagram te maken van de voorspellende variabele en de responsvariabele.
Als het spreidingsdiagram een lineair verband tussen de twee variabelen laat zien, is een eenvoudige lineaire regressie waarschijnlijk geschikt.
Als het spreidingsdiagram echter een kwadratisch, kubisch of ander kromlijnig patroon vertoont tussen de voorspeller en de responsvariabele, is het waarschijnlijk geschikter om kromlijnige regressie te gebruiken.
U kunt ook een eenvoudig lineair regressiemodel en een kromlijnig regressiemodel fitten en de aangepaste R-kwadraatwaarden van elk model vergelijken om te bepalen welk model het beste bij de gegevens past.
De aangepaste R-kwadraat is nuttig omdat deze u vertelt hoeveel van de variantie in de responsvariabele kan worden verklaard door de voorspellende variabele(n), aangepast voor het aantal voorspellende variabelen in het model.
Over het algemeen past het model met de hoogste aangepaste R-kwadraatwaarde beter bij de dataset.
Aanvullende bronnen
In de volgende tutorials wordt uitgelegd hoe u polynomiale regressie kunt uitvoeren in verschillende statistische software:
Een inleiding tot polynomiale regressie
Hoe polynomiale regressie uit te voeren in Excel
Hoe polynomiale regressie uit te voeren in Python
Hoe polynomiale regressie uit te voeren in R
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder