Hoe kruiscorrelatie in r te berekenen

Kruiscorrelatie is een manier om de mate van gelijkenis tussen een tijdreeks en een vertraagde versie van een andere tijdreeks te meten.

Dit type correlatie is handig om te berekenen, omdat het ons kan vertellen of waarden in de ene tijdreeks voorspellend zijn voor toekomstige waarden in een andere tijdreeks. Met andere woorden, het kan ons vertellen of de ene tijdreeks een voorlopende indicator is voor een andere tijdreeks.

Dit type correlatie wordt op veel verschillende gebieden gebruikt, waaronder:

Economie: De Consumer Confidence Index (CCI) wordt beschouwd als een voorlopende indicator van het bruto binnenlands product (bbp) van een land. Als de CCI bijvoorbeeld in een bepaalde maand hoog is, zal het bbp waarschijnlijk x maanden later hoger zijn.

Bedrijven: Marketinguitgaven worden vaak beschouwd als een voorlopende indicator van toekomstige bedrijfsinkomsten. Als een bedrijf bijvoorbeeld in een kwartaal een ongewoon hoog bedrag aan marketing uitgeeft, dan zou de totale omzet x kwartalen later hoog moeten zijn.

Biologie: De totale oceaanvervuiling wordt beschouwd als een voorlopende indicator van de populatie van een bepaalde soort schildpadden. Als de vervuiling bijvoorbeeld in een bepaald jaar hoger is, wordt verwacht dat de totale schildpaddenpopulatie x jaar later zal afnemen.

Het volgende voorbeeld laat zien hoe u de kruiscorrelatie tussen twee tijdreeksen in R kunt berekenen.

Voorbeeld: Hoe kruiscorrelatie in R te berekenen

Stel dat we de volgende tijdreeksen in R hebben die de totale marketinguitgaven (in duizenden) voor een bepaald bedrijf weergeven, evenals de totale inkomsten (in duizenden) gedurende 12 opeenvolgende maanden:

 #define data
marketing <- c(3, 4, 5, 5, 7, 9, 13, 15, 12, 10, 8, 8)
revenue <- c(21, 19, 22, 24, 25, 29, 30, 34, 37, 40, 35, 30)

We kunnen de kruiscorrelatie voor elke vertraging tussen de twee tijdreeksen als volgt berekenen met behulp van de ccf()- functie:

 #calculate cross correlation
ccf(marketing, revenue)

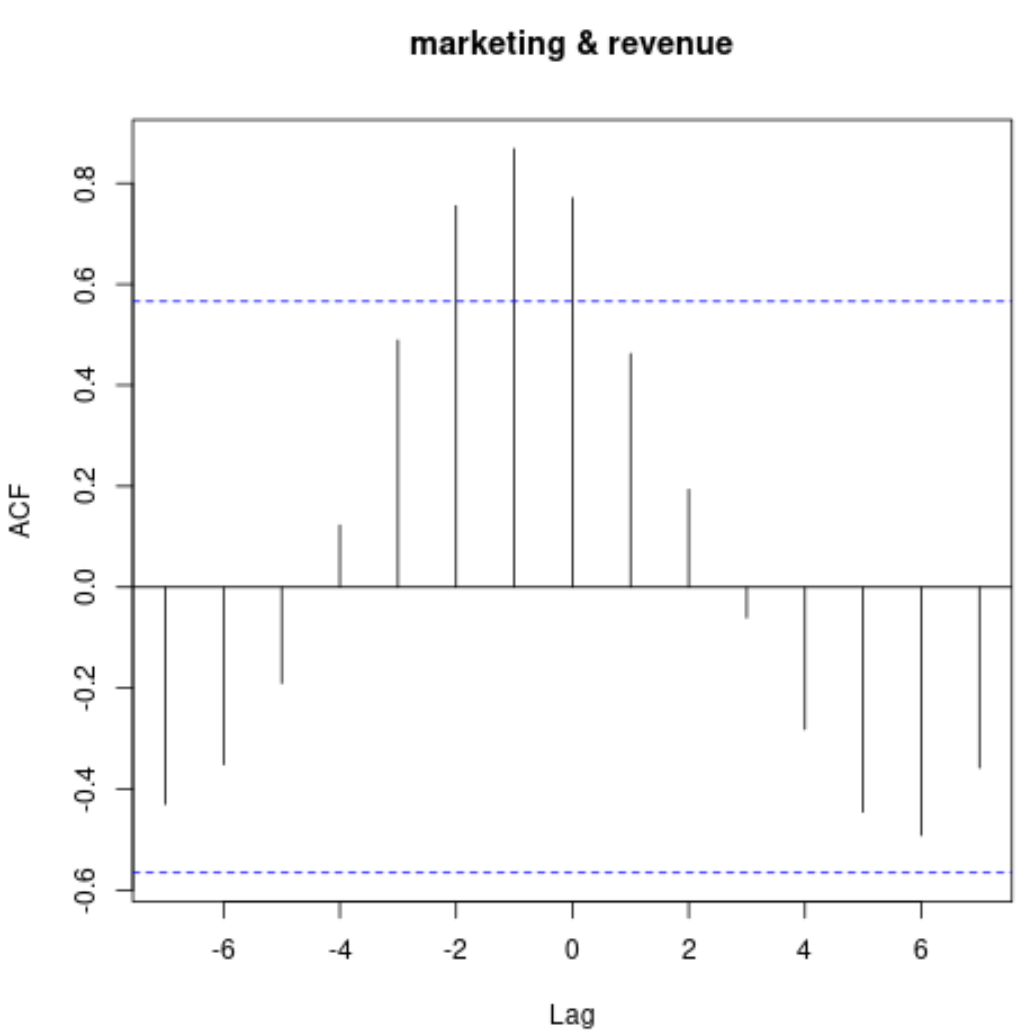
Deze grafiek toont de correlatie tussen de twee tijdreeksen met verschillende vertragingen.

Om de werkelijke correlatiewaarden weer te geven, kunnen we de volgende syntaxis gebruiken:

 #display cross correlation values
print (ccf(marketing, revenue))

Autocorrelations of series 'X', by lag

    -7 -6 -5 -4 -3 -2 -1 0 1 2 3 
-0.430 -0.351 -0.190 0.123 0.489 0.755 0.868 0.771 0.462 0.194 -0.061 
     4 5 6 7 
-0.282 -0.445 -0.492 -0.358

U kunt deze uitvoer als volgt interpreteren:

• De kruiscorrelatie bij lag 0 is 0,771 .
• De kruiscorrelatie bij lag 1 is 0,462 .
• De kruiscorrelatie bij lag 2 is 0,194 .
• De kruiscorrelatie bij lag 3 is -0,061 .

Enzovoort.

Merk op dat de correlatie tussen de twee tijdreeksen vrij positief is, met vertragingen van -2 tot 2, wat ons vertelt dat marketinguitgaven in een bepaalde maand behoorlijk voorspellend zijn voor de omzet één en twee maanden later.

Dit is intuïtief logisch: we verwachten dat hoge marketinguitgaven in een bepaalde maand voorspellend zullen zijn voor een hogere omzet in de komende twee maanden.

Aanvullende bronnen

Hoe autocorrelatie in R te berekenen
Hoe de gedeeltelijke correlatie in R te berekenen
Hoe de glijdende correlatie in R te berekenen