Hoe u een kruskal-wallis-test uitvoert in excel

Een Kruskal-Wallis-test wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de medianen van drie of meer onafhankelijke groepen. Het wordt beschouwd als het niet-parametrische equivalent van eenrichtings-ANOVA.

In deze tutorial wordt uitgelegd hoe u een Kruskal-Wallis-test uitvoert in Excel.

Voorbeeld: Kruskal-Wallis-test in Excel

Onderzoekers willen weten of drie verschillende meststoffen tot verschillende niveaus van plantengroei leiden. Ze selecteren willekeurig 30 verschillende planten en verdelen ze in drie groepen van 10, waarbij elke groep een andere meststof wordt toegediend. Na een maand meten ze de hoogte van elke plant.

Volg de volgende stappen om een Kruskal-Wallis-test uit te voeren om te bepalen of de mediane groei voor alle drie de groepen hetzelfde is.

Stap 1: Voer de gegevens in.

Voer de volgende gegevens in, die de totale groei (in inches) van elk van de tien planten in elke groep weergeven:

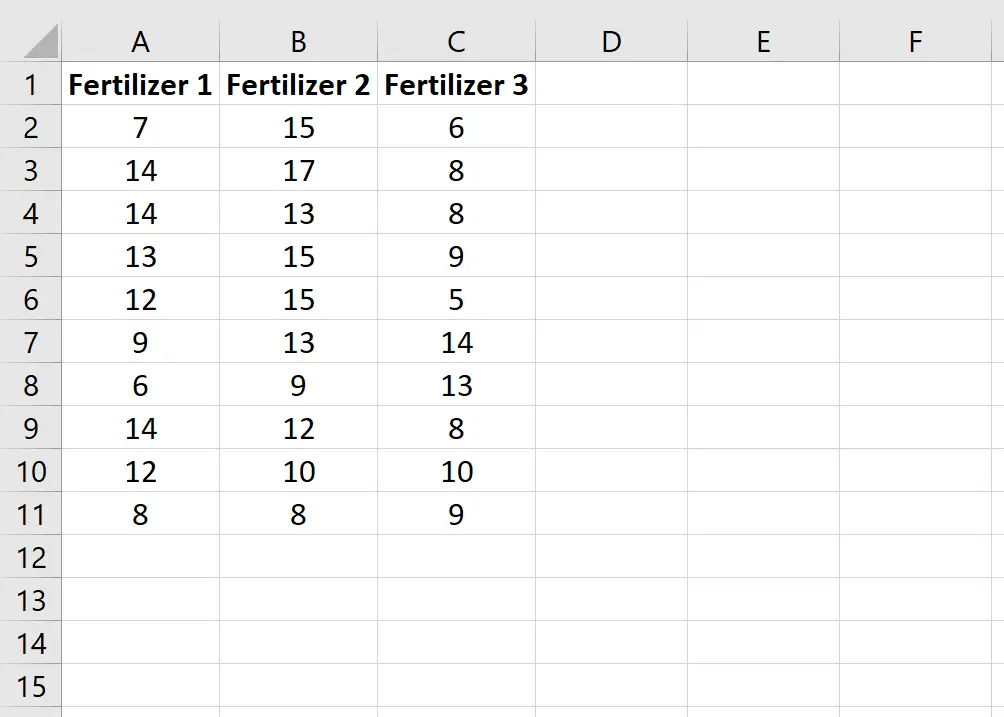
Stap 2: Classificeer de gegevens.

Vervolgens zullen we de functie RANK.AVG() gebruiken om een rangorde toe te kennen aan de groei van elke plant onder de 30 planten. De volgende formule laat zien hoe je de rangorde van de eerste plant in de eerste groep berekent:

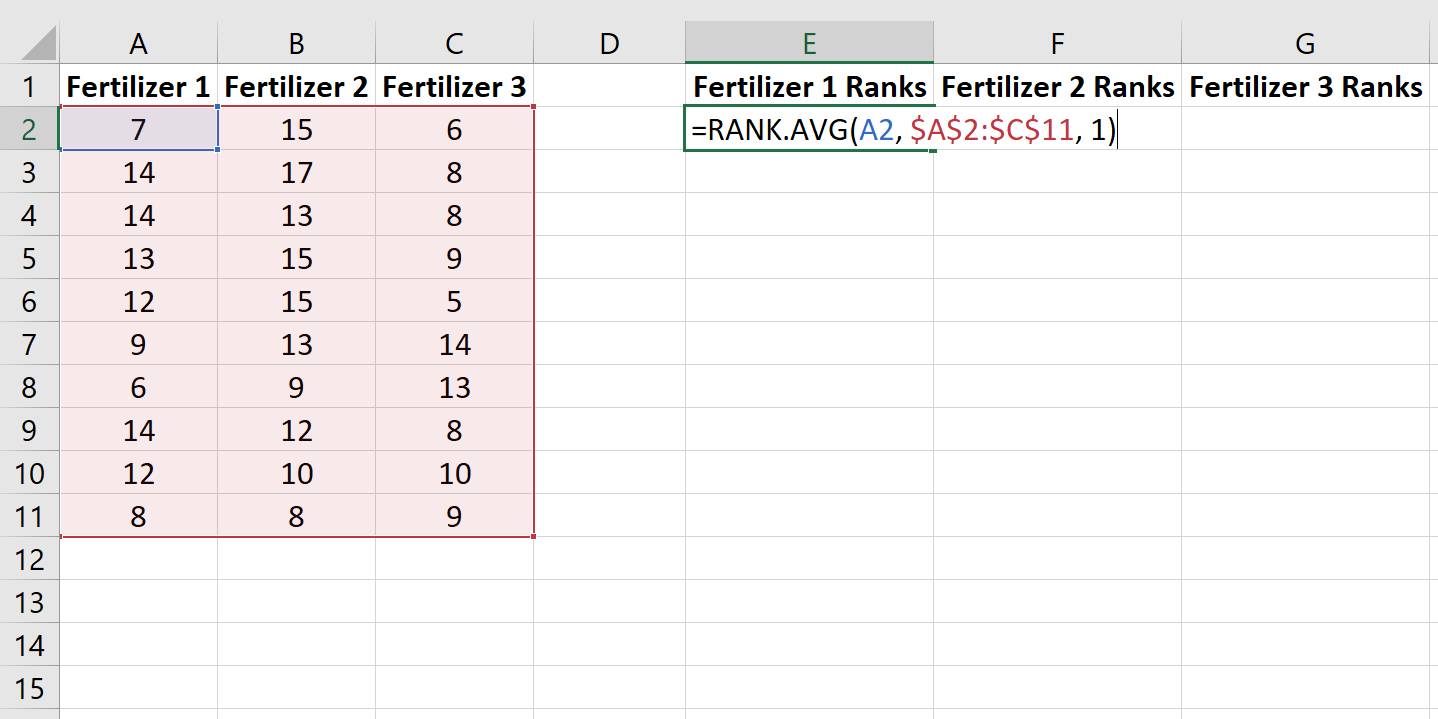
Kopieer deze formule naar de rest van de cellen:

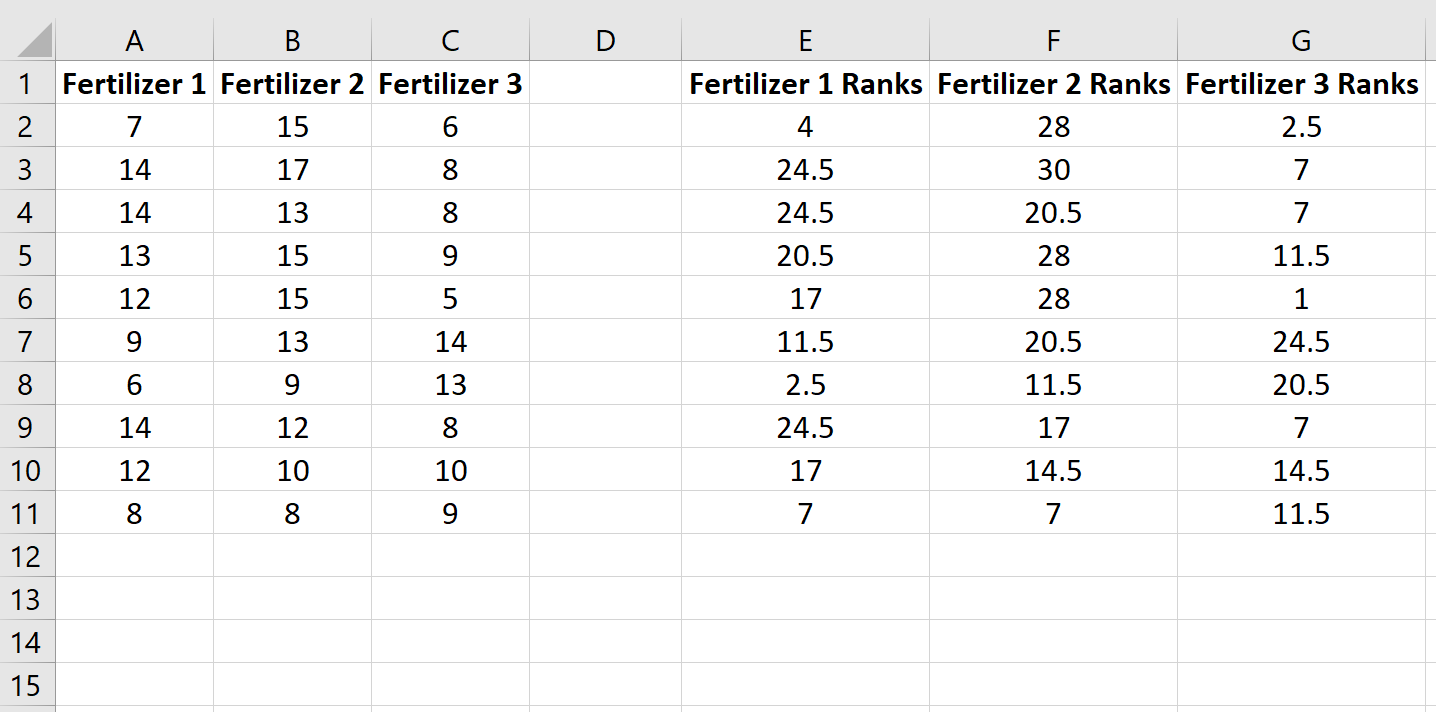
Bereken vervolgens de som van de rangen voor elke kolom, samen met de steekproefomvang en de kwadratische som van de rangen gedeeld door de steekproefomvang:

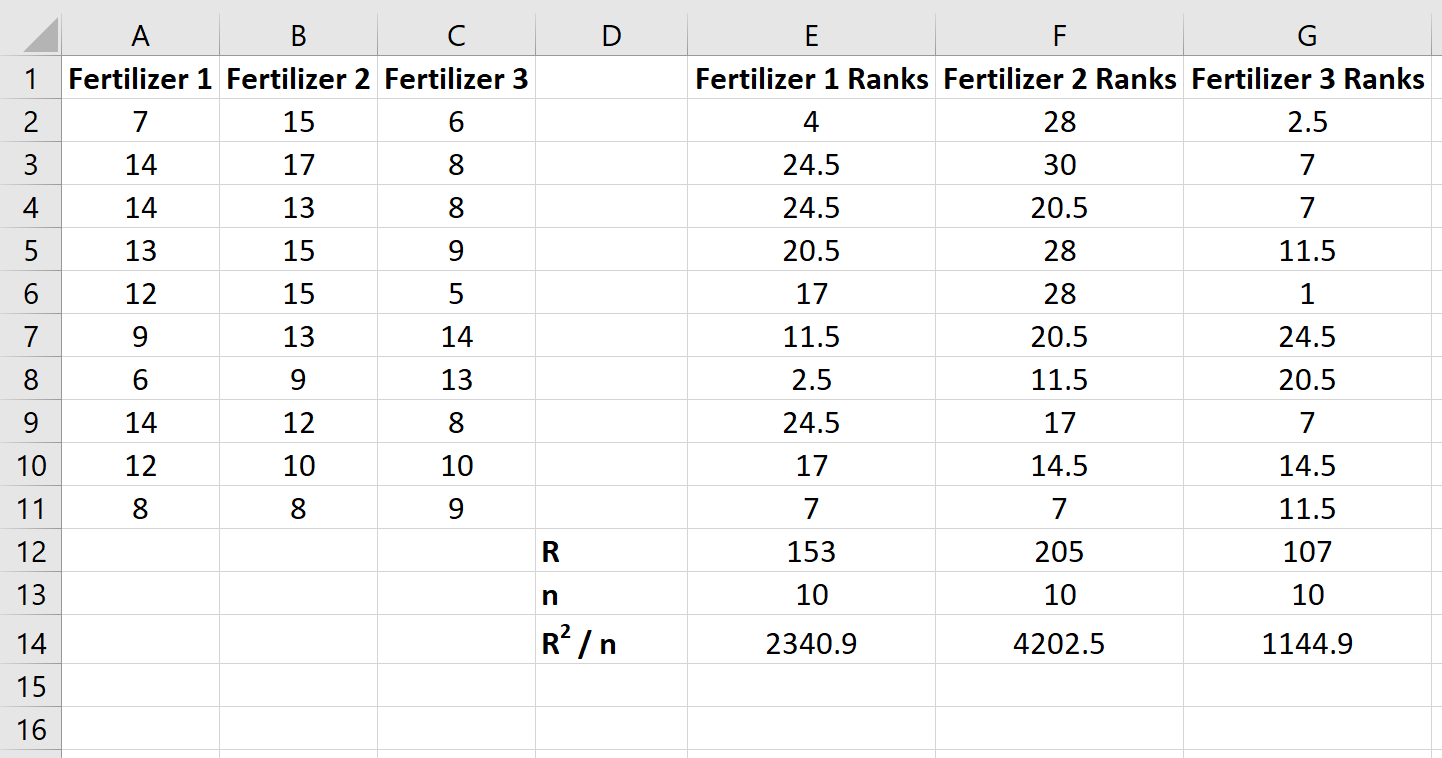
Stap 3: Bereken de teststatistiek en de bijbehorende p-waarde.

De teststatistiek wordt gedefinieerd als:

H = 12/(n(n+1)) * ΣR _j ² /n _j – 3(n+1)

Goud:

• n = totale steekproefomvang
• R _j ² = som van rangen voor de ^jde groep
• n _j = steekproefomvang van de ^j- de groep

Onder de nulhypothese volgt H een Chi-kwadraatverdeling met k-1 vrijheidsgraden.

De volgende schermafbeelding toont de formules die worden gebruikt om de teststatistiek, H, en de bijbehorende p-waarde te berekenen:

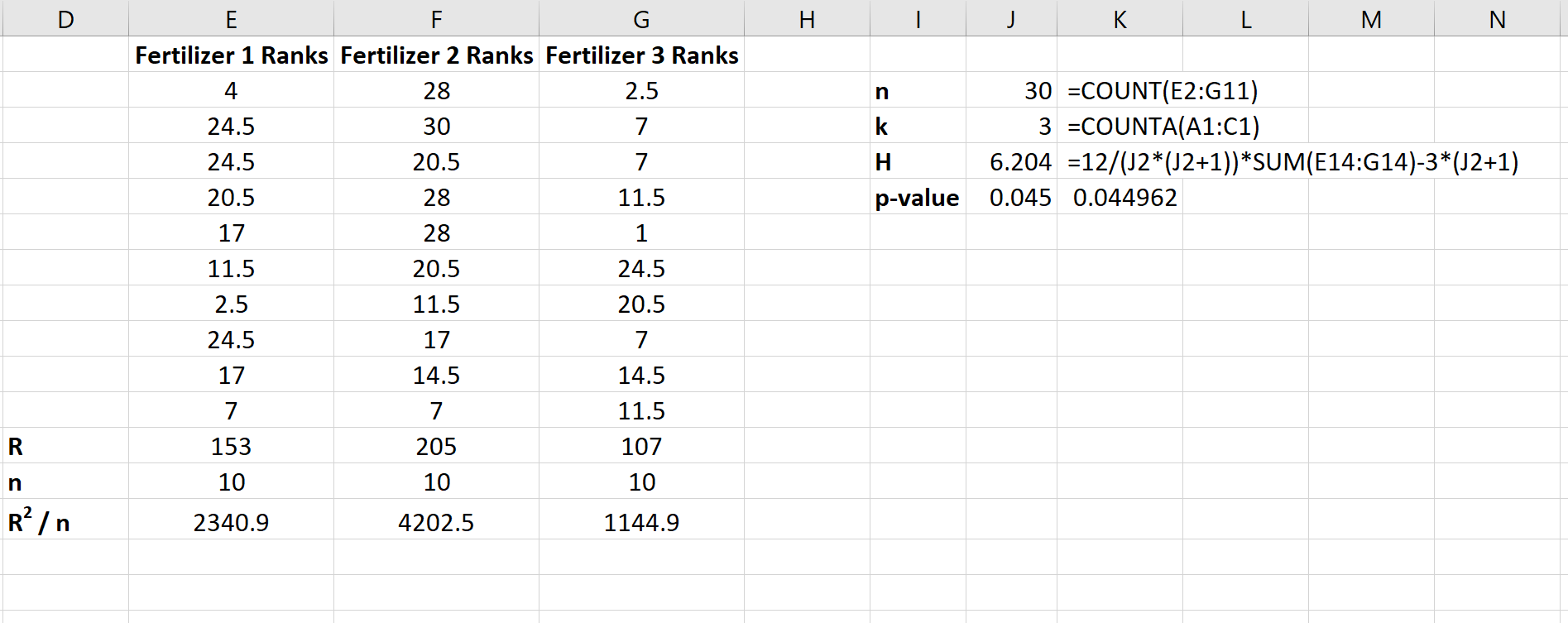
De teststatistiek is H = 6,204 en de overeenkomstige p-waarde is p = 0,045 . Omdat deze p-waarde kleiner is dan 0,05, kunnen we de nulhypothese verwerpen dat de gemiddelde plantengroei voor alle drie de meststoffen hetzelfde is. We hebben voldoende bewijs om te concluderen dat het type kunstmest dat wordt gebruikt statistisch significante verschillen in plantengroei veroorzaakt.

Stap 4: Rapporteer de resultaten.

Ten slotte willen we graag de resultaten van de Kruskal-Wallis-test melden. Hier is een voorbeeld van hoe u dit kunt doen:

Om te bepalen of de gemiddelde plantengroei hetzelfde was voor drie verschillende plantenmeststoffen, werd een Kruskal-Wallist-test uitgevoerd. In totaal zijn bij de analyse 30 planten gebruikt. Elke meststof werd op 10 verschillende planten toegepast.

Uit de test bleek dat de gemiddelde plantengroei niet hetzelfde was (H = 6,204, p = 0,045) tussen de drie meststoffen. Dat wil zeggen dat er een statistisch significant verschil was in de gemiddelde plantengroei tussen twee of meer meststoffen.