Hoe u een kruskal-wallis-test uitvoert in spss

Een Kruskal-Wallis-test wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de medianen van drie of meer onafhankelijke groepen. Het wordt beschouwd als het niet-parametrische equivalent van eenrichtings-ANOVA .

In deze tutorial wordt uitgelegd hoe u een Kruskal-Wallis-test uitvoert in SPSS.

Voorbeeld: Kruskal-Wallis-test in SPSS

Een onderzoeker wil weten of drie medicijnen verschillende effecten hebben op kniepijn. Daarom rekruteert hij dertig mensen die allemaal soortgelijke kniepijn ervaren en verdeelt ze willekeurig in drie groepen die medicijn 1, medicijn 2 of medicijn 3 krijgen.

Nadat ze het medicijn een maand hebben ingenomen, vraagt de onderzoeker aan ieder individu om de kniepijn te beoordelen op een schaal van 1 tot 100, waarbij 100 de ernstigste pijn aangeeft. Hieronder vindt u de scores van de 30 personen:

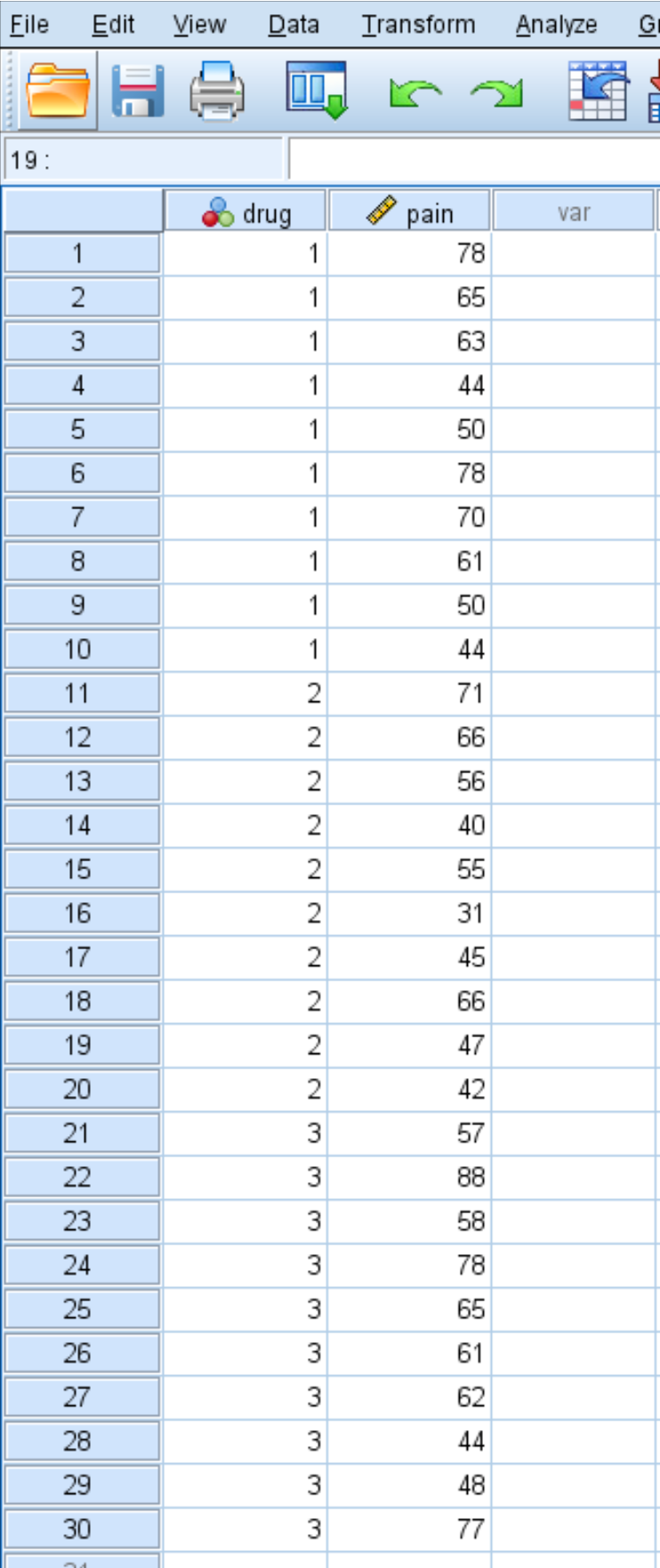
Volg de volgende stappen om een Kruskal-Wallis-test uit te voeren om te bepalen of er al dan niet een verschil is in de gerapporteerde kniepijnniveaus tussen de drie groepen:

Stap 1: Voer een Kruskal-Wallis-test uit.

Klik op het tabblad Analyseren , vervolgens op Niet-parametrische tests , vervolgens op Legacy Dialogs en vervolgens op K Independent Samples :

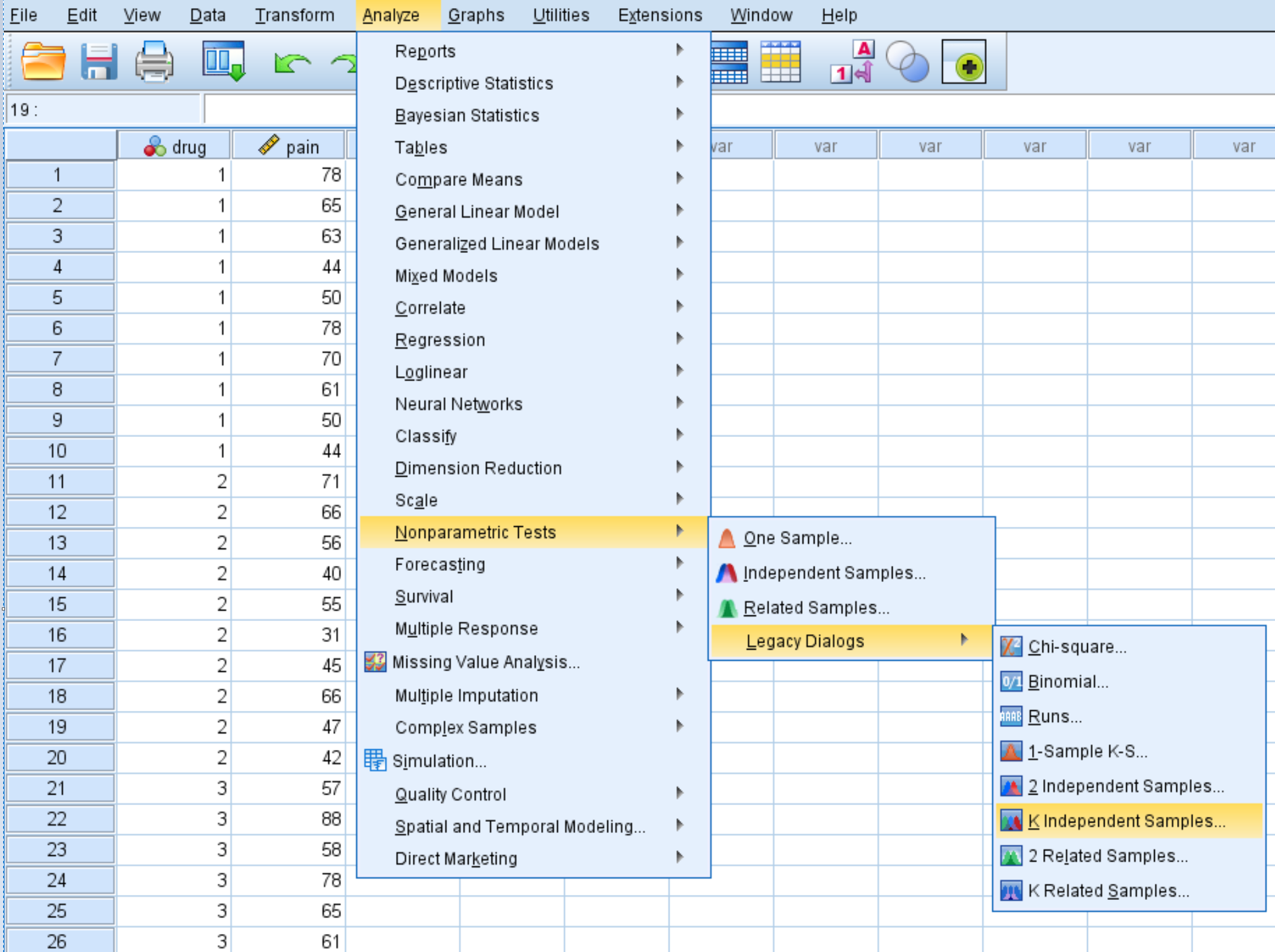
Sleep in het venster dat verschijnt de pijnvariabele naar het vak met de naam Testvariabelenlijst en Geneesmiddel in het vak met de naam Groeperingsvariabele. Klik vervolgens op Bereik instellen en stel de minimumwaarde in op 1 en de maximumwaarde op 3. Klik vervolgens op Doorgaan . Zorg ervoor dat het vakje naast Kruskal-Wallis H is aangevinkt en klik vervolgens op OK .

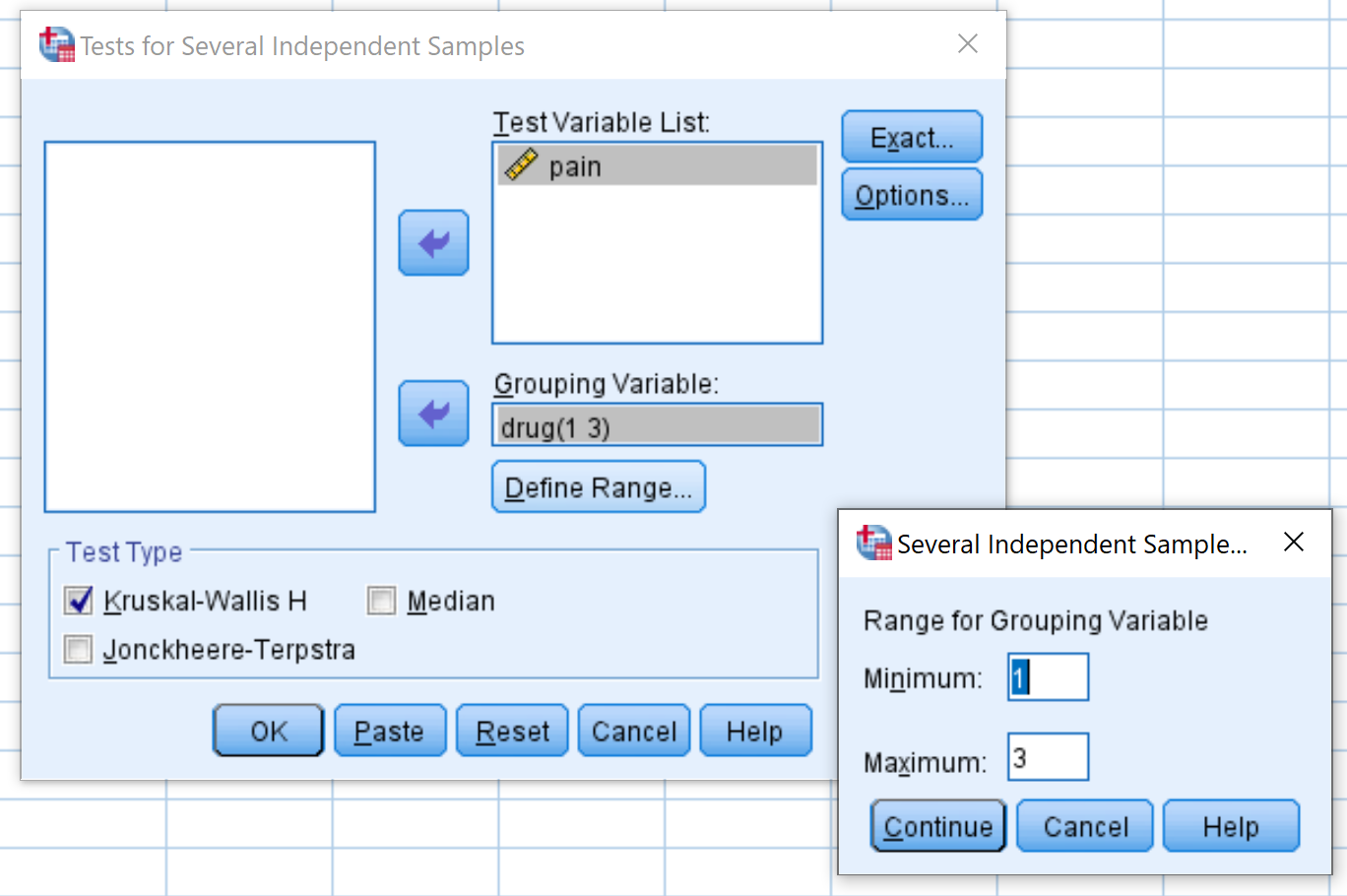
Stap 2: Interpreteer de resultaten.

Zodra u op OK klikt, verschijnen de Kruskal-Wallis-testresultaten:

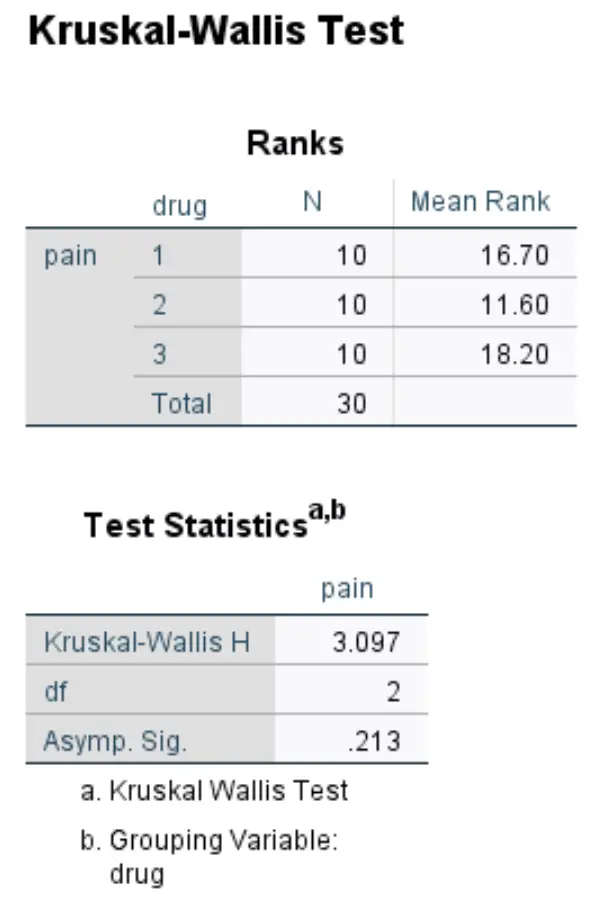
De tweede tabel in de uitvoer geeft de testresultaten weer:

• Kruskal-Wallis H: Dit is de X ^2- teststatistiek.
• df: Dit zijn de vrijheidsgraden, berekend als #groepen-1 = 3-1 = 2.
• Asympt. Sig: Dit is de p-waarde die hoort bij een X ^2- teststatistiek van 3,097 met 2 vrijheidsgraden. Dit kan ook worden gevonden met behulp van dechi-kwadraatscore naar P-waardecalculator.

Omdat de p-waarde (0,213) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet voldoende bewijs om te zeggen dat er een statistisch significant verschil bestaat in de beoordeling van kniepijn tussen deze drie groepen.