Hoe kwadratische regressie uit te voeren in r

Wanneer twee variabelen een lineair verband hebben, kunnen we vaak eenvoudige lineaire regressie gebruiken om hun verband te kwantificeren.

Wanneer twee variabelen echter een kwadratische relatie hebben, kunnen we kwadratische regressie gebruiken om hun relatie te kwantificeren.

In deze tutorial wordt uitgelegd hoe u kwadratische regressie uitvoert in R.

Voorbeeld: kwadratische regressie in R

Stel dat we de relatie willen begrijpen tussen het aantal gewerkte uren en het gerapporteerde geluk. We hebben de volgende gegevens over het aantal gewerkte uren per week en het gerapporteerde geluksniveau (op een schaal van 0 tot 100) voor 11 verschillende mensen:

Gebruik de volgende stappen om een kwadratisch regressiemodel in R te fitten.

Stap 1: Voer de gegevens in.

Eerst maken we een dataframe met onze gegevens:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Stap 2: Visualiseer de gegevens.

Vervolgens zullen we een eenvoudig spreidingsdiagram maken om de gegevens te visualiseren.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

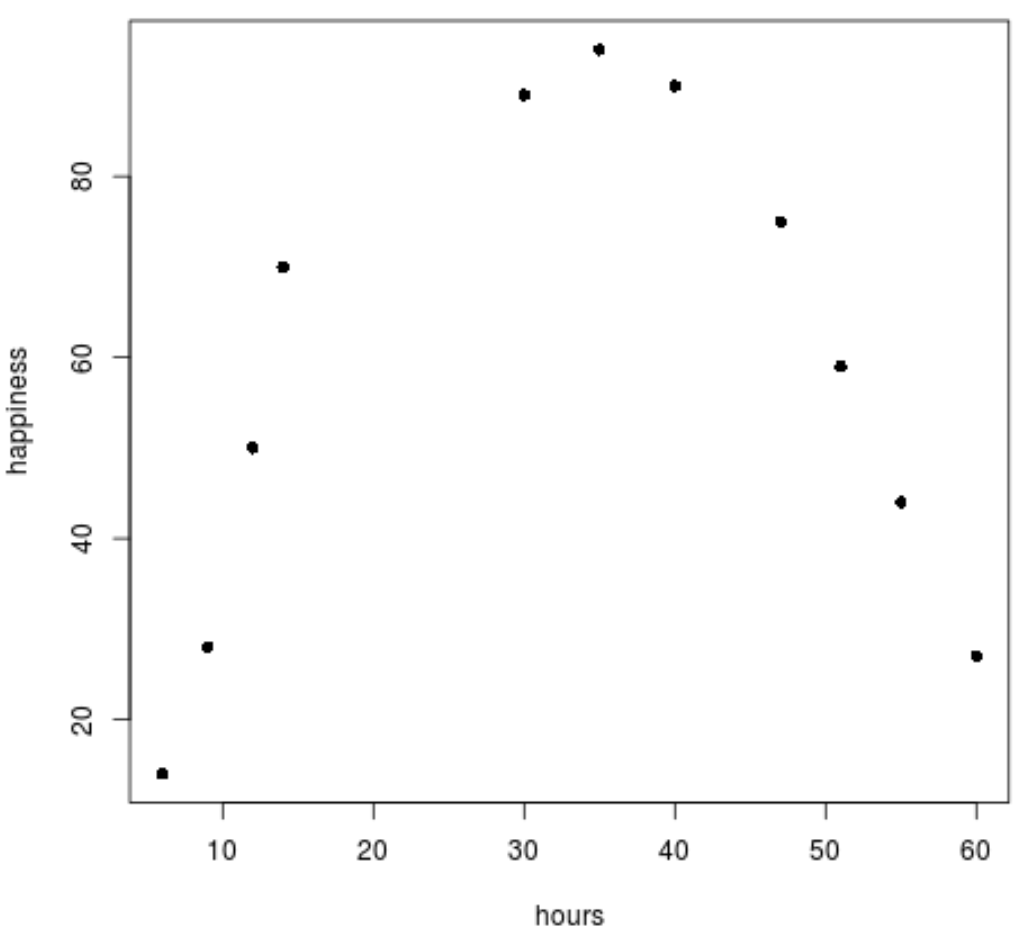
We kunnen duidelijk zien dat de gegevens geen lineair patroon volgen.

Stap 3: Pas een eenvoudig lineair regressiemodel toe.

Vervolgens passen we een eenvoudig lineair regressiemodel toe om te zien hoe goed het bij de gegevens past:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

De totale variantie in geluk die door het model wordt verklaard, bedraagt slechts 4,46% , zoals blijkt uit de meervoudige R-kwadraatwaarde.

Stap 4: Pas een kwadratisch regressiemodel toe.

Vervolgens passen we een kwadratisch regressiemodel toe.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

De totale variantie in geluk die door het model wordt verklaard, nam toe tot 96,02% .

We kunnen de volgende code gebruiken om te visualiseren hoe goed het model bij de gegevens past:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

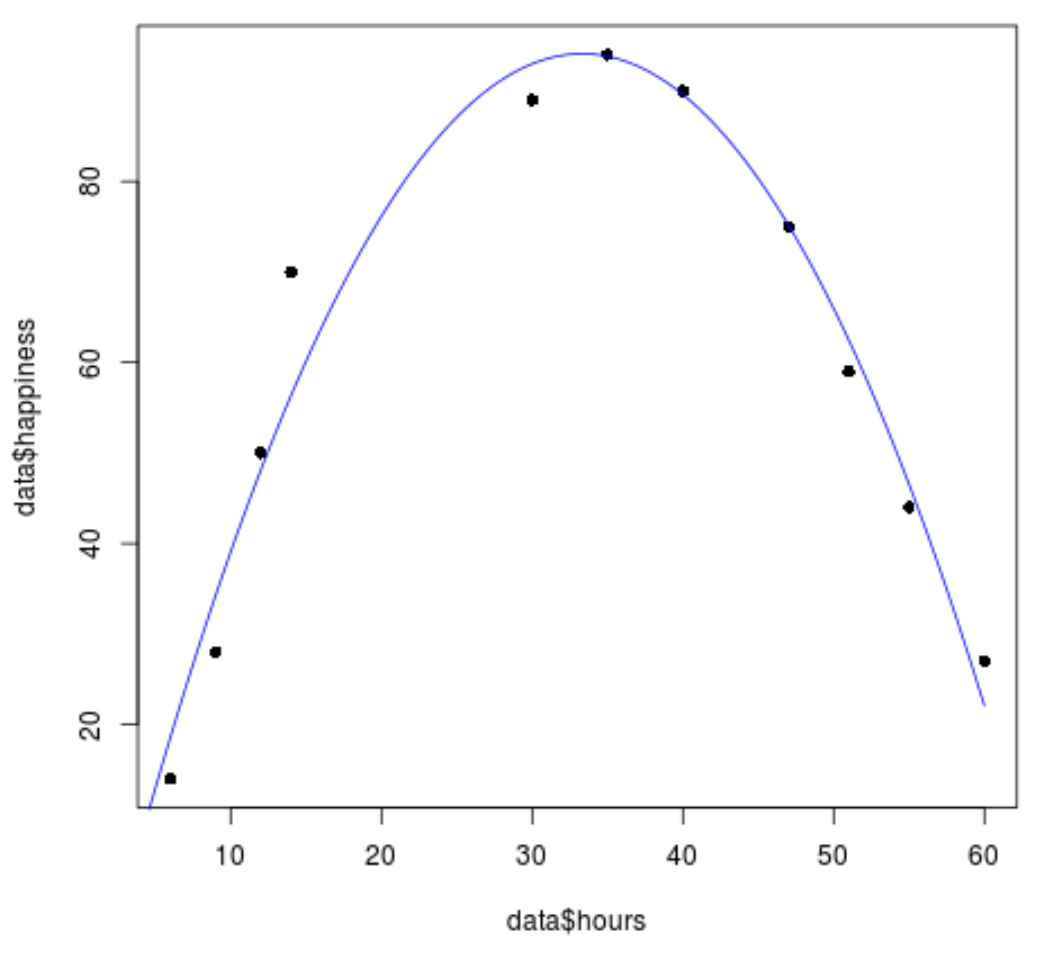
We kunnen zien dat de kwadratische regressielijn redelijk goed bij de gegevenswaarden past.

Stap 5: Interpreteer het kwadratische regressiemodel.

In de vorige stap zagen we dat het resultaat van het kwadratische regressiemodel was:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

Op basis van de hier gepresenteerde coëfficiënten zou de aangepaste kwadratische regressie zijn:

Geluk = -0,1012 (uren) ² + 6,7444 (uren) – 18,2536

We kunnen deze vergelijking gebruiken om het voorspelde geluk van een individu te vinden, gegeven het aantal uren dat hij of zij per week werkt.

Een persoon die bijvoorbeeld 60 uur per week werkt, zou een geluksniveau van 22,09 hebben:

Geluk = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Omgekeerd zou iemand die 30 uur per week werkt een geluksniveau van 92,99 moeten hebben:

Geluk = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99