Hoe kwadratische regressie uit te voeren in stata

Wanneer twee variabelen een lineair verband hebben, kunt u vaak eenvoudige lineaire regressie gebruiken om hun verband te kwantificeren.

Wanneer twee variabelen echter een kwadratische relatie hebben, kunt u kwadratische regressie gebruiken om hun relatie te kwantificeren.

In deze tutorial wordt uitgelegd hoe u kwadratische regressie uitvoert in Stata.

Voorbeeld: kwadratische regressie in Stata

Stel dat we de relatie tussen het aantal gewerkte uren en geluk willen begrijpen. We hebben de volgende gegevens over het aantal gewerkte uren per week en het gerapporteerde geluksniveau (op een schaal van 0 tot 100) voor 16 verschillende mensen:

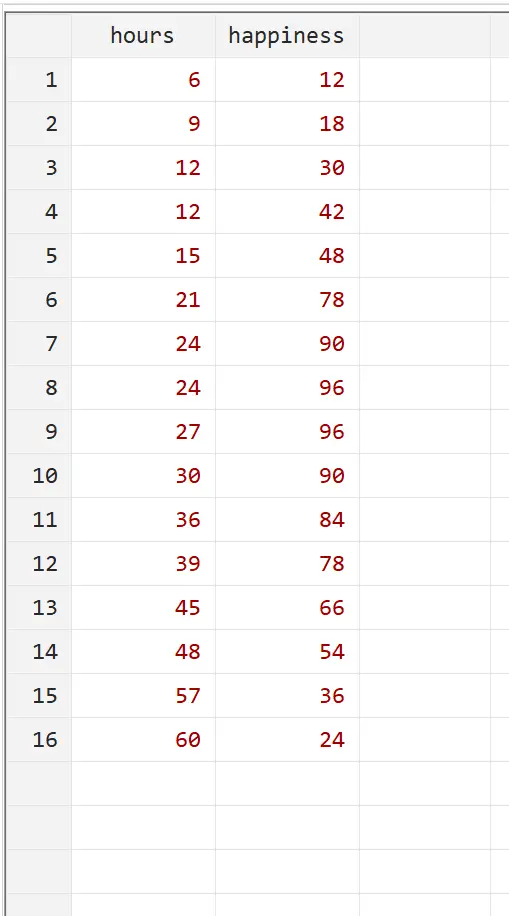
U kunt dit voorbeeld reproduceren door deze exacte gegevens in Stata in te voeren met behulp van Gegevens > Gegevenseditor > Gegevenseditor (Bewerken) in het hoofdmenu.

Gebruik de volgende stappen om kwadratische regressie uit te voeren in Stata.

Stap 1: Visualiseer de gegevens.

Voordat we kwadratische regressie kunnen gebruiken, moeten we ervoor zorgen dat de relatie tussen de verklarende variabele (uren) en de responsvariabele (geluk) inderdaad kwadratisch is. Laten we de gegevens dus visualiseren met behulp van een spreidingsdiagram door het volgende in het opdrachtvak te typen:

verspreid de uren van geluk

Dit levert het volgende spreidingsdiagram op:

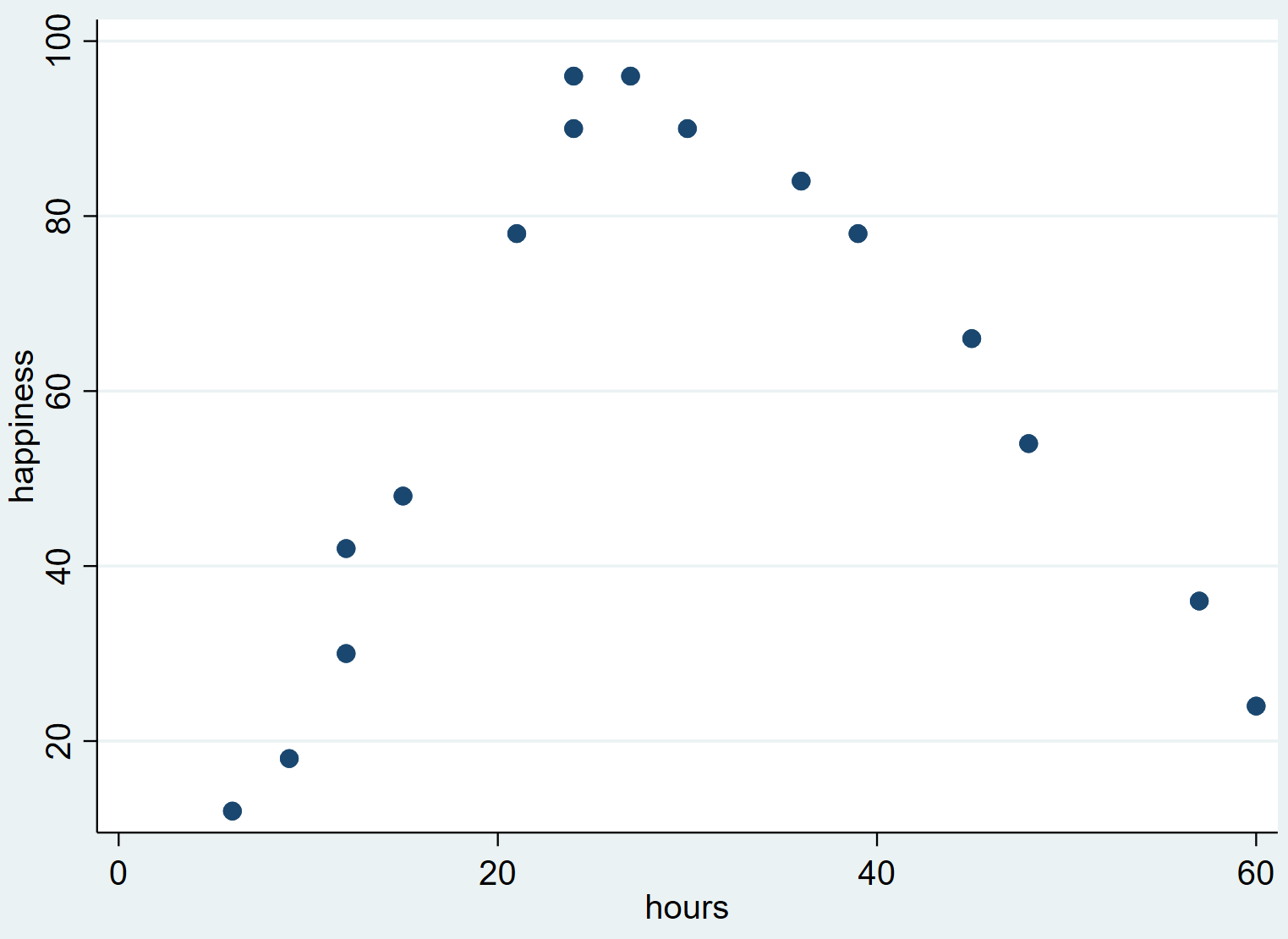
We kunnen zien dat het geluk de neiging heeft toe te nemen naarmate het aantal gewerkte uren toeneemt van nul tot een bepaald punt, maar vervolgens begint af te nemen naarmate het aantal gewerkte uren boven de 30 uitkomt.

Deze omgekeerde ‚U‘-vorm in het spreidingsdiagram geeft aan dat er een kwadratische relatie bestaat tussen gewerkte uren en geluk, wat betekent dat we kwadratische regressie moeten gebruiken om deze relatie te kwantificeren.

Stap 2: Voer kwadratische regressie uit.

Voordat we het kwadratische regressiemodel aan de gegevens aanpassen, moeten we een nieuwe variabele maken voor de kwadratische waarden van onze urenvoorspellingsvariabele . We kunnen dit doen door het volgende in het opdrachtvak te typen:

gen uren2 = uren*uren

We kunnen deze nieuwe variabele bekijken door in het hoofdmenu naar Gegevens > Gegevenseditor > Gegevenseditor (Bladeren) te gaan.

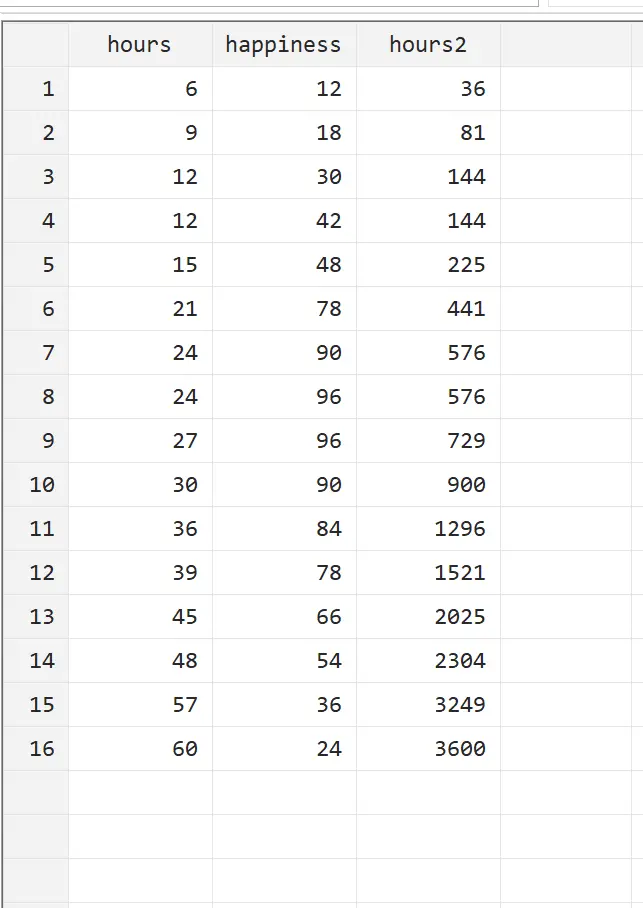
We kunnen zien dat uren2 eenvoudigweg uren in het kwadraat zijn. We kunnen nu een kwadratische regressie uitvoeren met uren en uren2 als verklarende variabelen en geluk als responsvariabele. Om een kwadratische regressie uit te voeren, typt u het volgende in het opdrachtvak:

regressie-uren van geluksuren2

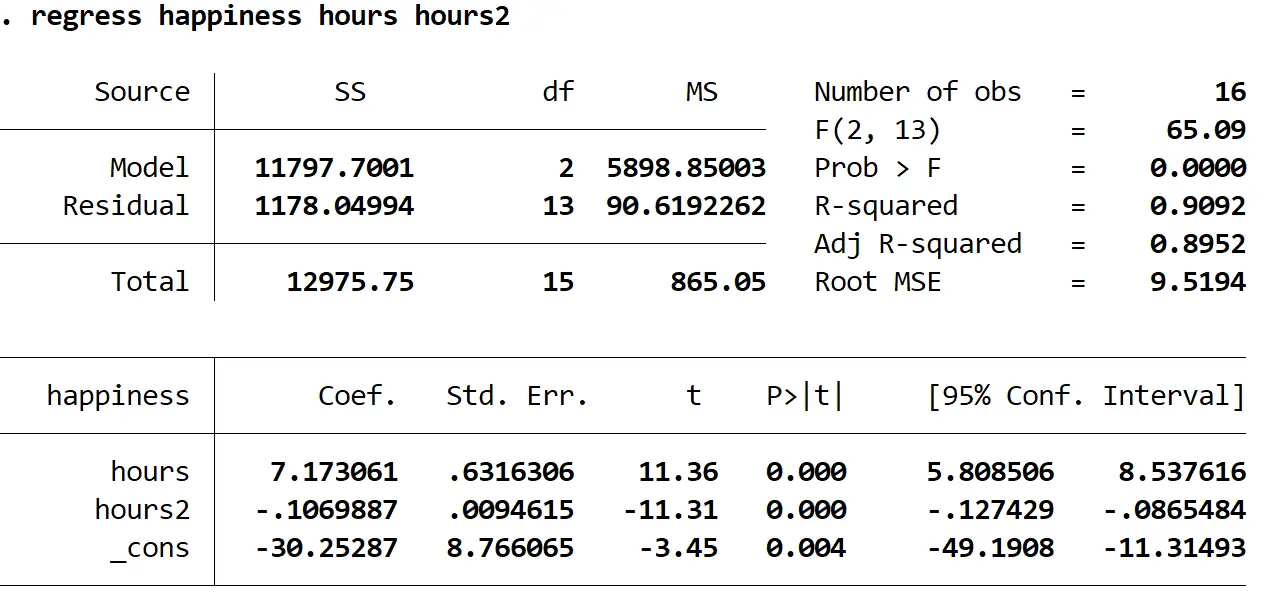
Zo interpreteert u de meest interessante cijfers in het resultaat:

Waarschijnlijk > F: 0,000. Dit is de p-waarde voor de algehele regressie. Omdat deze waarde kleiner is dan 0,05 betekent dit dat de voorspellende variabelen uren en uren ² samen een statistisch significante relatie hebben met de responsvariabele geluk .

R kwadraat: 0,9092. Dit is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabele. In dit voorbeeld kan 90,92% van de variatie in geluk verklaard worden door uren en uren ² .

Regressievergelijking: We kunnen een regressievergelijking vormen met behulp van de coëfficiëntwaarden die in de uitvoertabel worden weergegeven. In dit geval zou de vergelijking zijn:

voorspeld geluk = -30,25287 + 7,173061 (uren) – 0,1069887 ( ² uur)

We kunnen deze vergelijking gebruiken om het voorspelde geluk van een individu te vinden, gegeven het aantal uren dat hij of zij per week werkt.

Iemand die bijvoorbeeld 60 uur per week werkt, zou een geluksniveau van 14,97 moeten hebben:

voorspeld geluk = -30,25287 + 7,173061(60) – .1069887(60 ² ) = 14,97 .

Omgekeerd zou iemand die 30 uur per week werkt een geluksniveau van 88,65 moeten hebben:

voorspeld geluk = -30,25287 + 7,173061(30) – .1069887(30 ² ) = 88,65 .

Stap 3: Rapporteer de resultaten.

Ten slotte willen we de resultaten van onze kwadratische regressie rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een kwadratische regressie uitgevoerd om de relatie te kwantificeren tussen het aantal uren dat iemand werkte en het overeenkomstige geluksniveau (gemeten van 0 tot 100). Voor de analyse is gebruik gemaakt van een steekproef van 16 personen.

Uit de resultaten bleek dat er een statistisch significante relatie bestond tussen de verklarende variabelen uren en uur ² en de responsvariabele geluk (F(2, 13) = 65,09, p < 0,0001).

Samen waren deze twee verklarende variabelen verantwoordelijk voor 90,92% van de verklaarde variabiliteit in geluk.

De regressievergelijking bleek:

voorspeld geluk = -30,25287 + 7,173061 (uren) – 0,1069887 ( ² uur)