Hoe kwantielregressie uit te voeren in python

Lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te begrijpen.

Wanneer we lineaire regressie uitvoeren, willen we doorgaans de gemiddelde waarde van de responsvariabele schatten.

We zouden in plaats daarvan echter een methode kunnen gebruiken die bekend staat als kwantielregressie om elke kwantiel- of percentielwaarde van de responswaarde te schatten, zoals het 70e percentiel, 90e percentiel, 98e percentiel, enz.

Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u deze functie kunt gebruiken om kwantielregressie uit te voeren in Python.

Stap 1: Laad de benodigde pakketten

Eerst zullen we de benodigde pakketten en functies laden:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

Stap 2: Creëer de gegevens

Voor dit voorbeeld maken we een dataset aan met daarin de gestudeerde uren en behaalde examenresultaten voor 100 studenten aan een universiteit:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Stap 3: Voer kwantielregressie uit

Vervolgens passen we een kwantielregressiemodel toe met bestudeerde uren als voorspellende variabele en examenscores als responsvariabele.

We zullen het model gebruiken om het verwachte 90e percentiel van examenscores te voorspellen op basis van het aantal bestudeerde uren:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

Uit het resultaat kunnen we de geschatte regressievergelijking zien:

90e percentiel van examenscore = 59,6104 + 2,8495*(uren)

De 90e percentielscore van alle studenten die 8 uur studeren zou bijvoorbeeld 82,4 moeten zijn:

90e percentiel van examenscore = 59,6104 + 2,8495*(8) = 82,4 .

De uitvoer geeft ook de bovenste en onderste betrouwbaarheidsgrenzen weer voor het snijpunt en de tijden van de voorspellende variabele.

Stap 4: Visualiseer de resultaten

We kunnen de regressieresultaten ook visualiseren door een spreidingsdiagram te maken met de aangepaste kwantielregressievergelijking over de grafiek heen:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

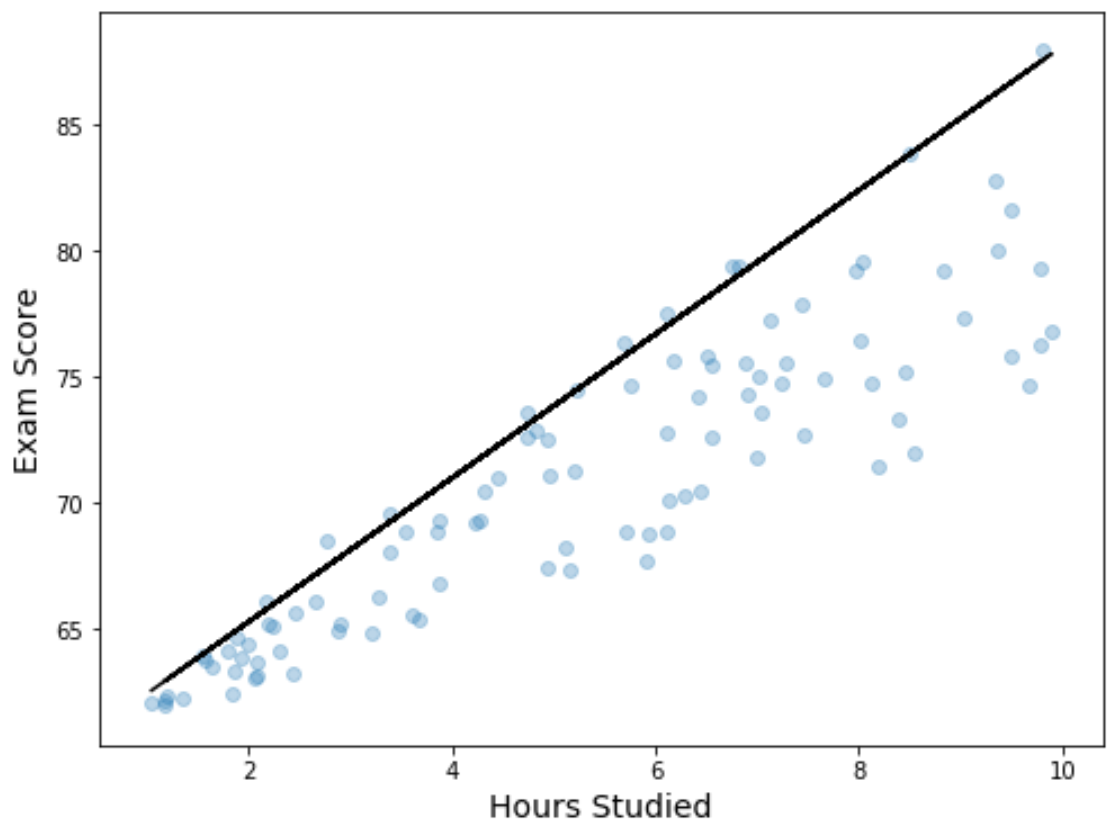
In tegenstelling tot een eenvoudige lineaire regressielijn moet u er rekening mee houden dat deze aangepaste lijn niet de „best passende lijn“ voor de gegevens vertegenwoordigt. In plaats daarvan passeert het het geschatte 90e percentiel op elk niveau van de voorspellende variabele.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in Python
Hoe kwadratische regressie uit te voeren in Python