Hoe kwantielregressie uit te voeren in r

Lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te begrijpen.

Wanneer we lineaire regressie uitvoeren, willen we doorgaans de gemiddelde waarde van de responsvariabele schatten.

We zouden in plaats daarvan echter een methode kunnen gebruiken die bekend staat als kwantielregressie om elke kwantiel- of percentielwaarde van de responswaarde te schatten, zoals het 70e percentiel, 90e percentiel, 98e percentiel, enz.

Om kwantielregressie in R uit te voeren, kunnen we de functie rq() uit het quantreg- pakket gebruiken, die de volgende syntaxis gebruikt:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

Goud:

• y: de responsvariabele
• x: de voorspellende variabele(n)
• data: de naam van de dataset
• tau: Het percentiel dat moet worden gevonden. De standaardwaarde is de mediaan (tau = 0,5), maar u kunt deze instellen op elk getal tussen 0 en 1.

Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u deze functie kunt gebruiken om kwantielregressie uit te voeren in R.

Stap 1: Voer de gegevens in

Voor dit voorbeeld gaan we een dataset aanmaken met daarin de gestudeerde uren en behaalde examenresultaten voor 100 verschillende studenten aan een universiteit:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Stap 2: Voer kwantielregressie uit

Vervolgens passen we een kwantielregressiemodel toe met bestudeerde uren als voorspellende variabele en examenscores als responsvariabele.

We zullen het model gebruiken om het verwachte 90e percentiel van examenscores te voorspellen op basis van het aantal bestudeerde uren:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

Uit het resultaat kunnen we de geschatte regressievergelijking zien:

Examenscore 90e percentiel = 60,25 + 2,437*(uren)

De 90e percentielscore voor alle studenten die 8 uur studeren zou bijvoorbeeld 79,75 moeten zijn:

90e percentiel van examenscore = 60,25 + 2,437*(8) = 79,75 .

De uitvoer geeft ook de bovenste en onderste betrouwbaarheidsgrenzen weer voor het snijpunt en de tijden van de voorspellende variabele.

Stap 3: Visualiseer de resultaten

We kunnen de regressieresultaten ook visualiseren door een spreidingsdiagram te maken met de aangepaste kwantielregressievergelijking over de grafiek heen:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

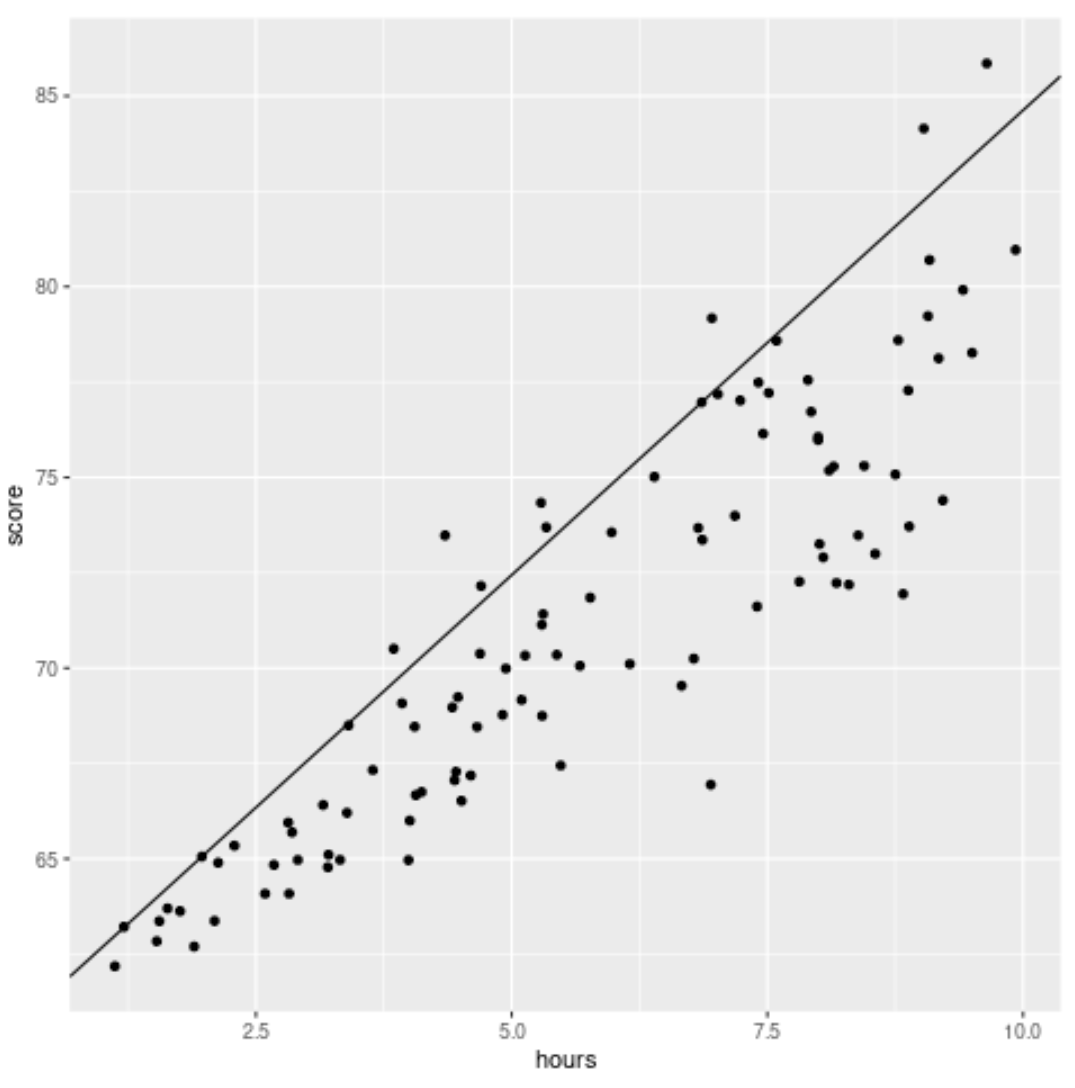
In tegenstelling tot een traditionele lineaire regressielijn moet u er rekening mee houden dat deze aangepaste lijn niet door het hart van de gegevens loopt. In plaats daarvan passeert het het geschatte 90e percentiel op elk niveau van de voorspellende variabele.

We kunnen het verschil zien tussen de aangepaste kwantielregressievergelijking en de eenvoudige lineaire regressievergelijking door het argument geom_smooth() toe te voegen:

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

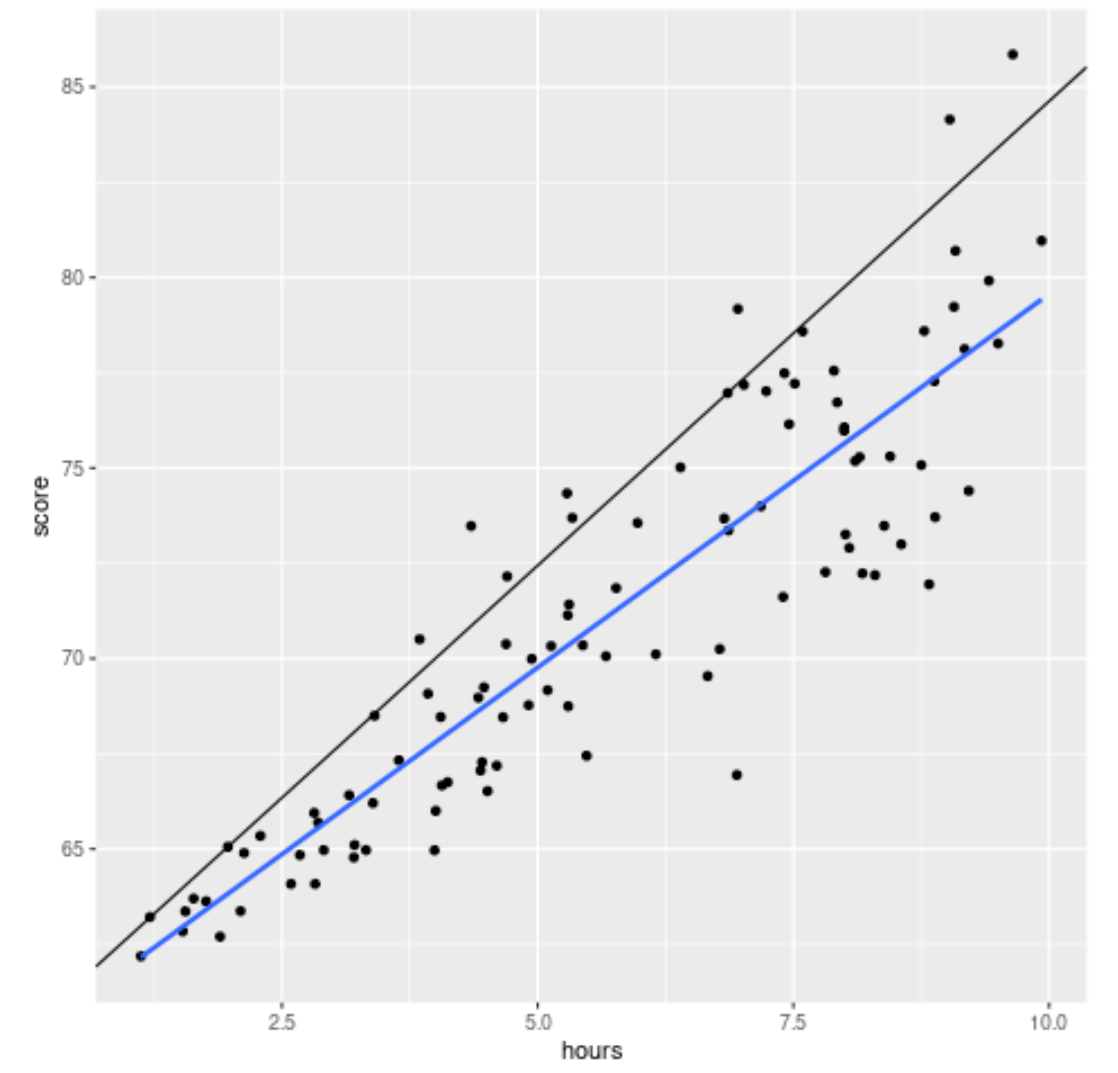
De zwarte lijn geeft de kwantielregressielijn weer, aangepast voor het 90e percentiel, en de blauwe lijn geeft de eenvoudige lineaire regressielijn weer, die de gemiddelde waarde van de responsvariabele schat.

Zoals verwacht loopt de eenvoudige lineaire regressielijn door de gegevens en toont ons de geschatte gemiddelde waarde van examenscores op elk uurniveau.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe kwadratische regressie uit te voeren in R