Kwartielen

In dit artikel leggen we uit wat kwartielen zijn. U vindt de definitie van elk kwartiel, hoe u deze kunt berekenen en enkele concrete voorbeelden. We laten u ook zien hoe u kwartielen voor gegroepeerde gegevens kunt berekenen. Bovendien kunt u kwartielen van elke dataset berekenen met een online rekenmachine.

Wat zijn kwartielen?

In de statistieken zijn kwartielen de drie waarden die een reeks geordende gegevens in vier gelijke delen verdelen. Het eerste, tweede en derde kwartiel vertegenwoordigen dus respectievelijk 25%, 50% en 75% van alle statistische gegevens.

Kwartielen worden weergegeven door een hoofdletter Q en de kwartielindex, dus het eerste kwartiel is Q ₁ , het tweede kwartiel is Q ₂ en het derde kwartiel is Q ₃ .

👉 U kunt de onderstaande rekenmachine gebruiken om kwartielen van elke dataset te berekenen.

Opgemerkt moet worden dat kwartielen een maatstaf zijn voor de niet-centrale positie, op dezelfde manier als kwintielen, decielen en percentielen. U kunt op deze webpagina controleren wat elk van deze kwantieltypen is.

eerste kwartiel

Het eerste kwartiel , ook wel kwartiel 1 genoemd, is de waarde groter dan 25% van de statistische gegevens in een steekproef. Met andere woorden: het eerste kwartiel vertegenwoordigt meer dan 25% van de waargenomen gegevens.

Het eerste kwartiel wordt uitgedrukt door het symbool Q ₁ en wordt gebruikt om de kleinste gegevenswaarden in de steekproef aan te duiden.

tweede kwartiel

Het tweede kwartiel , ook wel kwartiel 2 genoemd, is de waarde groter dan 50% van de statistische gegevens in een steekproef. Daarom verdeelt het tweede kwartiel de dataset in twee helften en valt samen met de mediaan en het vijfde deciel.

Het symbool voor het tweede kwartiel is _Q2 .

derde kwartiel

Het derde kwartiel , ook wel het 3e kwartiel genoemd, is de waarde die groter is dan 75% van de statistische gegevens in een steekproef. Met andere woorden: het derde kwartiel vertegenwoordigt meer dan 75% van de verzamelde gegevens.

Het derde kwartiel wordt uitgedrukt door het symbool Q ₃ en vertegenwoordigt de grootste waarden in de steekproef.

Hoe kwartielen te berekenen

Om de positie van de kwartielen van een statistische gegevensset te berekenen , moet u het aantal kwartielen vermenigvuldigen met de som van het totale aantal gegevens plus één en het resultaat delen door vier.

De formule voor de kwartielen is daarom als volgt:

Let op: deze formule vertelt ons de positie van het kwartiel, niet de waarde van het kwartiel. Het kwartiel zijn de gegevens die zich bevinden op de positie die door de formule wordt verkregen.

Soms geeft het resultaat van deze formule ons echter een decimaal getal. We moeten daarom twee gevallen onderscheiden, afhankelijk van of het resultaat een decimaal getal is of niet:

• Als het resultaat van de formule een getal zonder decimaal deel is, zijn het kwartiel de gegevens die zich op de positie bevinden die door de bovenstaande formule wordt aangegeven.
• Als het resultaat van de formule een getal met een decimaal deel is, wordt de kwartielwaarde berekend met behulp van de volgende formule:

Waar x _i en x _i+1 de getallen zijn van de posities waartussen het getal verkregen door de eerste formule zich bevindt, en d het decimale deel is van het getal verkregen door de eerste formule.

Misschien is het berekenen van kwartielen erg ingewikkeld voor je, omdat er met veel dingen rekening moet worden gehouden. Maar aan de hand van de twee voorbeelden in het volgende gedeelte zul je zien hoe het eigenlijk heel eenvoudig is.

Opmerking : in de wetenschappelijke gemeenschap bestaat er geen consensus over hoe je kwartielen moet berekenen, dus je kunt een statistiekboek vinden waarin het iets anders wordt uitgelegd.

Voorbeelden van het berekenen van kwartielen

Om volledig te begrijpen hoe kwartielen worden berekend, vind je hieronder twee opgeloste oefeningen. In het eerste geval zijn de kwartielen gehele getallen en in het tweede geval zijn de kwartielen decimale getallen, zodat je kunt zien welke twee gevallen je kunt vinden.

voorbeeld 1

• Bereken de drie kwartielen van de volgende gegevensset:

Zoals we hierboven zagen, is de formule voor het bepalen van kwartielen:

In dit geval n is het totale aantal waarnemingen 15, we moeten daarom n vervangen door 15 en k door 1 om het eerste kwartiel te vinden:

Daarom is het eerste kwartiel het getal op positie vier van de geordende lijst met waarden, wat in dit geval 39 is.

Op dezelfde manier berekenen we het tweede kwartiel door de coëfficiënt k te vervangen door een 2:

Kwartiel 2 is dus het achtste getal in de gesorteerde lijst, wat overeenkomt met de waarde 48.

Tenslotte passen we nog een laatste keer de formule toe met k =3 om het derde kwartiel te berekenen:

Kwartiel 3 komt overeen met de gegevens op de twaalfde positie, namelijk 60.

Voorbeeld 2

• Zoek de drie kwartielen van de volgende gegevensreeksen:

In dit tweede voorbeeld hebben we 24 waarnemingen, dus de getallen verkregen uit de kwartielformule zijn decimaal.

We berekenen eerst de positie van het eerste kwartiel door k te vervangen door 1 in de algemene formule:

Maar we hebben het decimale getal 6,25, dus het eerste kwartiel ligt tussen de zesde en zevende data, die respectievelijk 22 en 25 zijn. Om het exacte kwartiel te berekenen, moeten we daarom de volgende formule toepassen:

In dit geval is x _i gelijk aan 22, x _i+1 25 en is d het decimale deel van het verkregen getal, dat wil zeggen 0,25. Nog:

Nu doen we dezelfde procedure om het tweede kwartiel te vinden:

Opnieuw krijgen we een decimaal getal uit de formule, in dit geval is het 12,5. We moeten daarom dezelfde formule gebruiken met het twaalfde en dertiende getal in de gegevenstabel, wat overeenkomt met 49 en 50:

Ten slotte herhalen we hetzelfde proces om het derde kwartiel te verkrijgen:

Maar het getal 18,75 ligt tussen het getal 18 en 19, dus het derde kwartiel zal tussen de waarden van deze posities (71 en 73) liggen. Om precies te zijn, dit is de waarde die we verkrijgen uit de volgende uitdrukking:

kwartiel rekenmachine

Sluit een statistische gegevensset aan op de onderstaande rekenmachine om kwartielen te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Kwartielen in gegroepeerde gegevens

Om kwartielen te berekenen wanneer gegevens in intervallen zijn gegroepeerd, moeten we eerst het interval of de bak vinden waarin het kwartiel valt met behulp van de volgende formule:

Het kwartiel zal zich daarom in het interval bevinden waarvan de absolute cumulatieve frequentie onmiddellijk groter is dan het getal verkregen met de vorige uitdrukking.

En zodra we weten tot welk interval het kwartiel behoort, moeten we de volgende formule toepassen om de exacte waarde van het kwartiel te vinden:

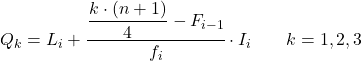
Goud:

• _Li is de ondergrens van het interval waarin het kwartiel ligt.
• n is het totale aantal waarnemingen.
• Fi _-1 is de cumulatieve absolute frequentie van het vorige interval.
• _fi is de absolute frequentie van het interval waarin het kwartiel ligt.
• I _i is de breedte van het kwartielinterval.

Als voorbeeld is hier een oefening om kwartielen in een reeks gegroepeerde gegevens te berekenen:

Om het eerste kwartiel te berekenen, moet u eerst het interval bepalen waarin dit valt. Om dit te doen, passen we de volgende formule toe:

Het eerste kwartiel bevindt zich dus in het interval waarvan de cumulatieve absolute frequentie onmiddellijk groter is dan 7,75, in dit geval is het het interval [50,60) waarvan de cumulatieve absolute frequentie 15 is. En zodra we het kwartielinterval kennen, gebruiken we de tweede procesformule :

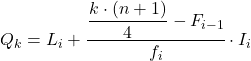
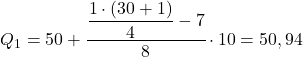
We passen dezelfde procedure opnieuw toe om het tweede kwartiel te verkrijgen. We bepalen eerst het interval waar het kwartiel ligt:

Het interval waarvan de cumulatieve absolute frequentie onmiddellijk groter is dan 15,5 is [60,70), met een cumulatieve absolute frequentie van 26. Het tweede kwartiel is daarom:

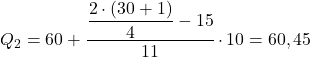
En ten slotte herhalen we het proces om het derde kwartiel te vinden. We berekenen eerst het interval dat het kwartiel bevat:

De cumulatieve absolute frequentie onmiddellijk boven 23,25 is 26, dus het derde kwartielbereik is [60,70). We passen daarom de formule toe om het kwartiel met dit interval te berekenen:

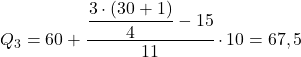
Waar worden kwartielen voor gebruikt?

Kwartielen zijn een maatstaf voor de positie, dus worden ze gebruikt om te weten hoe gegevens zijn gepositioneerd. Met andere woorden: de waarden van de drie kwartielen stellen ons in staat te weten of een willekeurig gegevensitem in de steekproef erg groot, erg klein is of dat het een gemiddelde waarde is.

Als we willekeurig een stukje data uit de steekproef nemen, kunnen we zien of de waarde ervan hoog of laag is door het te vergelijken met de kwartielen. Als de willekeurige gegevenswaarde kleiner is dan het eerste kwartiel, zal het een kleine waarde zijn, maar als de waarde groter is dan het derde kwartiel, zal het een grote waarde zijn. Evenzo, als de waarde van genoemde gegevens tussen het eerste en het derde kwartiel ligt, is het een tussenliggende waarde.

Aan de andere kant worden kwartielen ook gebruikt om andere statistische maatstaven te berekenen, zoals het interkwartielbereik (of interkwartielbereik), en om diagrammen te maken, zoals de box- enwhiskerplot (of boxplot).