Inleiding tot lasso-regressie

Bij gewone meervoudige lineaire regressie gebruiken we een reeks p- voorspellingsvariabelen en een responsvariabele om in een model van de vorm te passen:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Goud:

• Y : De responsvariabele
• _Xj : de j ^-de voorspellende variabele
• _βj : Het gemiddelde effect op Y van een toename van één eenheid in _Xj , waarbij alle andere voorspellers vast blijven
• ε : De foutterm

De waarden van β ₀ , β ₁ , B ₂ , …, β _p worden gekozen met behulp van de kleinste kwadratenmethode , die de som van de kwadraten van de residuen (RSS) minimaliseert:

RSS = Σ(y _i – ŷ _i ) ²

Goud:

• Σ : Een Grieks symbool dat som betekent
• y _i : de werkelijke responswaarde voor de ^i-de waarneming
• ŷ _i : De voorspelde responswaarde op basis van het meervoudige lineaire regressiemodel

Wanneer voorspellende variabelen echter sterk gecorreleerd zijn, kan multicollineariteit een probleem worden. Dit kan schattingen van modelcoëfficiënten onbetrouwbaar maken en een hoge variantie vertonen. Dat wil zeggen dat wanneer het model wordt toegepast op een nieuwe dataset die het nog nooit eerder heeft gezien, het waarschijnlijk slecht zal presteren.

Eén manier om dit probleem te omzeilen is door een methode te gebruiken die bekend staat als lasso regressie , die in plaats daarvan het volgende probeert te minimaliseren:

RSS + λΣ|β _j |

waarbij j van 1 naar p gaat en λ ≥ 0.

Deze tweede term in de vergelijking staat bekend als de opnameboete .

Wanneer λ = 0 heeft deze strafterm geen effect en levert lasso-regressie dezelfde coëfficiëntschattingen op als de kleinste kwadraten.

Naarmate λ echter de oneindigheid nadert, wordt de verwijderingsstraf invloedrijker en worden voorspellende variabelen die niet in het model geïmporteerd kunnen worden, tot nul teruggebracht en sommige zelfs uit het model verwijderd.

Waarom Lasso-regressie gebruiken?

Het voordeel van lasso-regressie ten opzichte van regressie met de kleinste kwadraten is de afweging tussen bias en variantie .

Bedenk dat Mean Square Error (MSE) een metriek is die we kunnen gebruiken om de nauwkeurigheid van een bepaald model te meten en die als volgt wordt berekend:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Variantie + Bias ² + Onherleidbare fout

Het basisidee van lasso-regressie is om een kleine vertekening te introduceren, zodat de variantie aanzienlijk kan worden verminderd, wat leidt tot een lagere algehele MSE.

Om dit te illustreren, bekijken we de volgende grafiek:

Merk op dat naarmate λ toeneemt, de variantie aanzienlijk afneemt met een zeer kleine toename van de bias. Vanaf een bepaald punt neemt de variantie echter minder snel af en leidt de afname van de coëfficiënten tot een significante onderschatting ervan, wat leidt tot een scherpe toename van de bias.

We kunnen uit de grafiek zien dat de MSE van de test het laagst is als we een waarde voor λ kiezen die een optimale afweging tussen vertekening en variantie oplevert.

Wanneer λ = 0 heeft de strafterm bij lasso-regressie geen effect en levert daarom dezelfde coëfficiëntschattingen op als de kleinste kwadraten. Door λ echter tot een bepaald punt te verhogen, kunnen we de algehele MSE van de test verminderen.

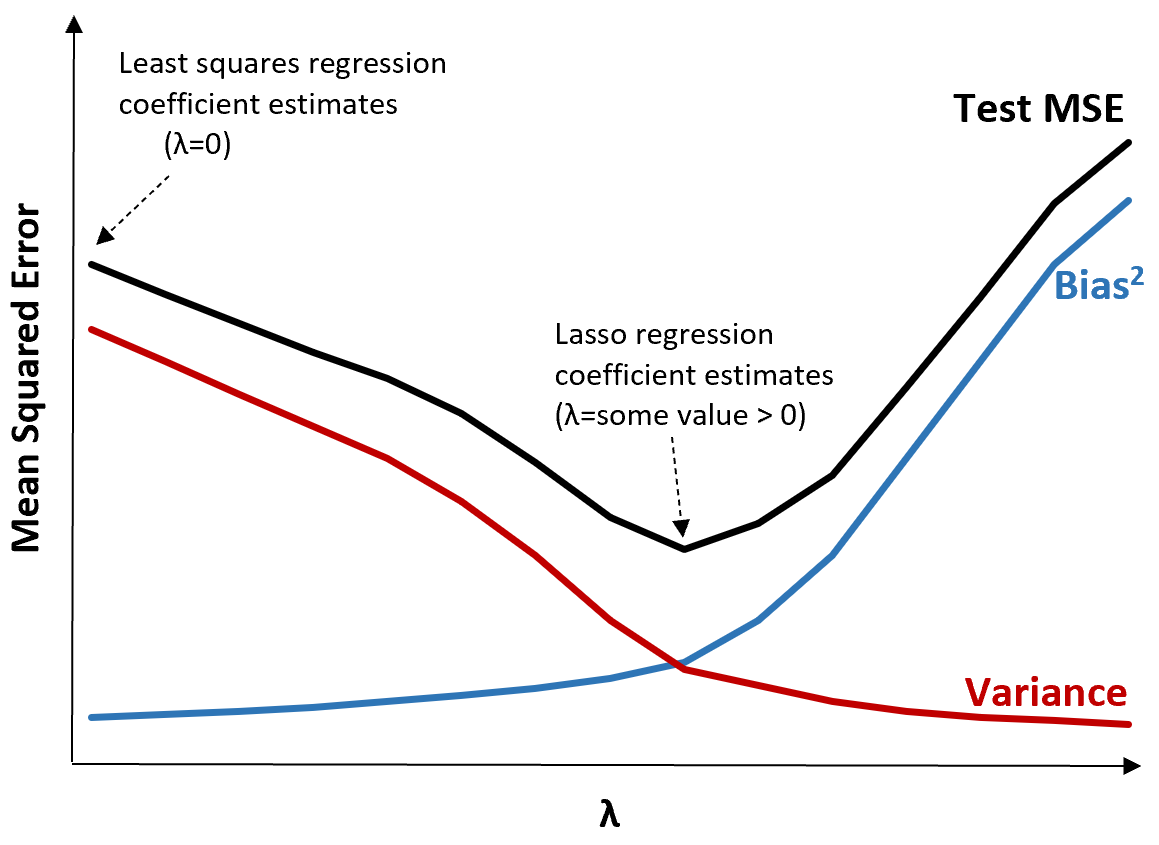
Dit betekent dat modelaanpassing door middel van lasso-regressie kleinere testfouten zal opleveren dan modelaanpassing door middel van kleinste-kwadratenregressie.

Lasso-regressie versus Ridge-regressie

Lasso-regressie en Ridge-regressie staan beide bekend als regularisatiemethoden omdat ze allebei proberen de resterende kwadratensom (RSS) en een bepaalde strafterm te minimaliseren.

Met andere woorden, ze beperken of regulariseren de schattingen van de modelcoëfficiënten.

De strafvoorwaarden die zij gebruiken zijn echter iets anders:

• Lasso-regressie probeert RSS + λΣ|β _j | te minimaliseren
• Ridge-regressie probeert RSS + λΣβ _j ² te minimaliseren

Wanneer we ridge-regressie gebruiken, worden de coëfficiënten van elke voorspeller teruggebracht tot nul, maar geen enkele kan volledig naar nul gaan.

Omgekeerd, als we lasso-regressie gebruiken, is het mogelijk dat sommige coëfficiënten volledig nul worden als λ groot genoeg wordt.

In technische termen is lasso-regressie in staat ‘sparse’ modellen te produceren, dat wil zeggen modellen die slechts een subset van voorspellende variabelen bevatten.

Dit roept de vraag op: is ridge-regressie of lasso-regressie beter?

Het antwoord: het hangt ervan af!

In gevallen waarin slechts een klein aantal voorspellende variabelen significant is, werkt lasso-regressie doorgaans beter omdat het in staat is om onbelangrijke variabelen volledig tot nul terug te brengen en ze uit het model te verwijderen.

Wanneer echter veel voorspellende variabelen significant zijn in het model en hun coëfficiënten ongeveer gelijk zijn, werkt nokregressie meestal beter omdat alle voorspellers in het model blijven.

Om te bepalen welk model het meest effectief is in het maken van voorspellingen, voeren we k-voudige kruisvalidatie uit. Welk model ook de laagste gemiddelde kwadratische fout (MSE) oplevert, is het beste model om te gebruiken.

Stappen om een lasso-regressie in de praktijk uit te voeren

De volgende stappen kunnen worden gebruikt om een lasso-regressie uit te voeren:

Stap 1: Bereken de correlatiematrix en VIF-waarden voor de voorspellende variabelen.

Eerst moeten we een correlatiematrix maken en de VIF-waarden (variantie-inflatiefactor) voor elke voorspellende variabele berekenen.

Als we een sterke correlatie detecteren tussen de voorspellende variabelen en hoge VIF-waarden (sommige teksten definiëren een „hoge“ VIF-waarde als 5, terwijl andere 10 gebruiken), dan is lasso-regressie waarschijnlijk geschikt.

Als er echter geen multicollineariteit in de gegevens aanwezig is, is het wellicht niet nodig om lasso-regressie uit te voeren. In plaats daarvan kunnen we gewone regressie met de kleinste kwadraten uitvoeren.

Stap 2: Pas het lasso-regressiemodel aan en kies een waarde voor λ.

Zodra we hebben vastgesteld dat lasso-regressie geschikt is, kunnen we het model aanpassen (met behulp van populaire programmeertalen zoals R of Python) met behulp van de optimale waarde voor λ.

Om de optimale waarde voor λ te bepalen, kunnen we meerdere modellen fitten met verschillende waarden voor λ en λ kiezen als de waarde die de laagste MSE-test oplevert.

Stap 3: Vergelijk lasso-regressie met ridge-regressie en gewone regressie met de kleinste kwadraten.

Ten slotte kunnen we ons lasso-regressiemodel vergelijken met een ridge-regressiemodel en een kleinste kwadraten-regressiemodel om te bepalen welk model de laagste MSE-test oplevert met behulp van k-voudige kruisvalidatie.

Afhankelijk van de relatie tussen de voorspellende variabelen en de responsvariabele is het heel goed mogelijk dat een van deze drie modellen in verschillende scenario’s beter presteert dan de andere.

Lasso-regressie in R & Python

In de volgende tutorials wordt uitgelegd hoe u lasso-regressie uitvoert in R en Python:

Lasso-regressie in R (stap voor stap)
Lasso-regressie in Python (stap voor stap)