Lasso-regressie in r (stap voor stap)

Lasso-regressie is een methode die we kunnen gebruiken om een regressiemodel te fitten wanneer multicollineariteit in de gegevens aanwezig is.

In een notendop probeert regressie met de kleinste kwadraten coëfficiëntschattingen te vinden die de resterende som van de kwadraten (RSS) minimaliseren:

RSS = Σ(y _i – ŷ _i )2

Goud:

• Σ : Een Grieks symbool dat som betekent
• y _i : de werkelijke responswaarde voor de ^i-de waarneming
• ŷ _i : De voorspelde responswaarde op basis van het meervoudige lineaire regressiemodel

Omgekeerd probeert lasso-regressie het volgende te minimaliseren:

RSS + λΣ|β _j |

waarbij j van 1 naar p voorspellende variabelen gaat en λ ≥ 0.

Deze tweede term in de vergelijking staat bekend als de opnameboete . Bij lasso-regressie selecteren we een waarde voor λ die de laagst mogelijke MSE-test (mean square error) oplevert.

Deze tutorial biedt een stapsgewijs voorbeeld van hoe u een lasso-regressie uitvoert in R.

Stap 1: Gegevens laden

Voor dit voorbeeld gebruiken we de ingebouwde dataset van R, genaamd mtcars . We zullen hp gebruiken als de responsvariabele en de volgende variabelen als voorspellers:

• mpg
• gewicht
• shit
• qsec

Om lasso-regressie uit te voeren, zullen we functies uit het glmnet- pakket gebruiken. Dit pakket vereist dat de responsvariabele een vector is en dat de set voorspellende variabelen van de klasse data.matrix is.

De volgende code laat zien hoe u onze gegevens kunt definiëren:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Stap 2: Pas het Lasso-regressiemodel toe

Vervolgens zullen we de functie glmnet() gebruiken om het lasso-regressiemodel aan te passen en alpha=1 te specificeren.

Houd er rekening mee dat het instellen van alfa op 0 gelijk is aan het gebruik van nokregressie en het instellen van alfa op een waarde tussen 0 en 1 gelijk is aan het gebruik van een elastisch net.  

Om te bepalen welke waarde we voor lambda moeten gebruiken, zullen we k-voudige kruisvalidatie uitvoeren en de lambda-waarde identificeren die de laagste testgemiddelde kwadratische fout (MSE) oplevert.

Merk op dat de functie cv.glmnet() automatisch een k-voudige kruisvalidatie uitvoert met behulp van k = 10 keer.

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

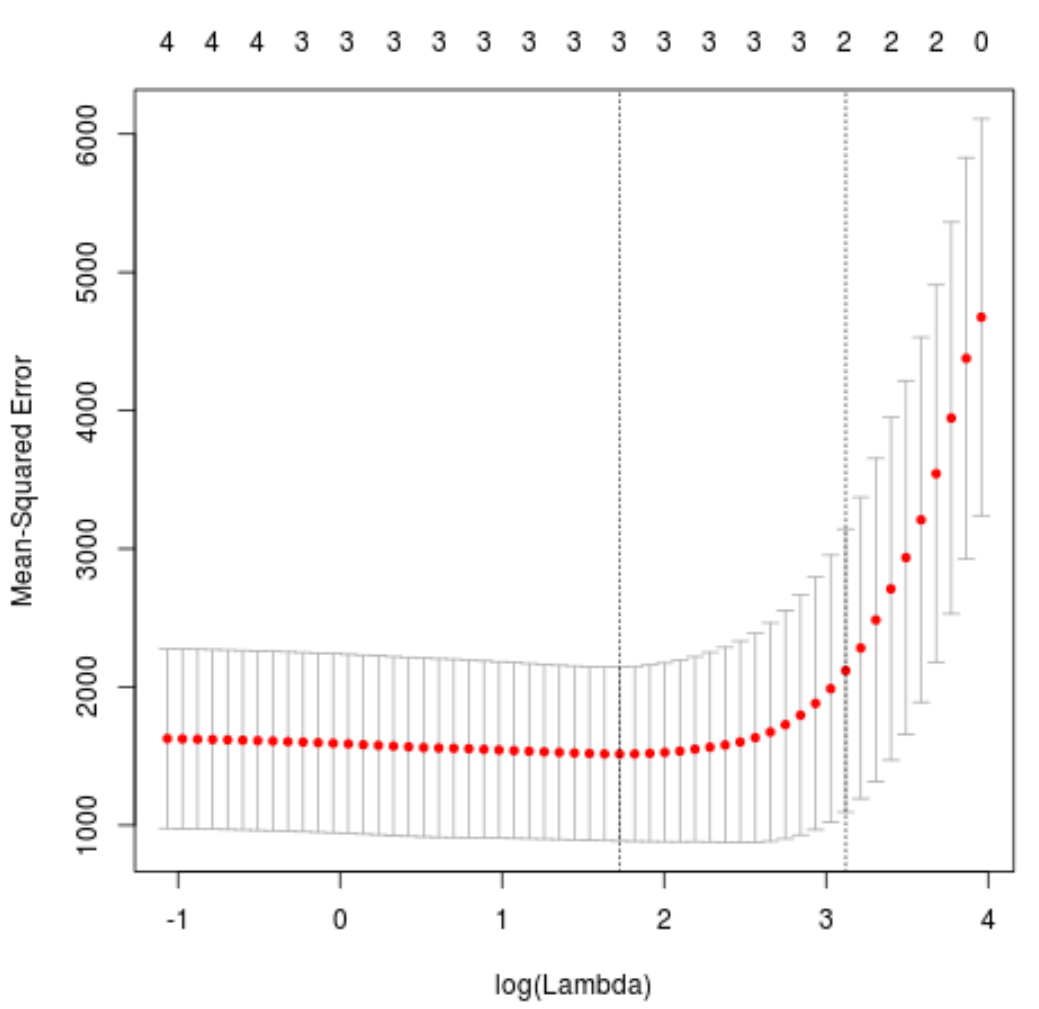
De lambdawaarde die de MSE-test minimaliseert blijkt 5,616345 te zijn.

Stap 3: Analyseer het uiteindelijke model

Ten slotte kunnen we het uiteindelijke model analyseren dat wordt geproduceerd door de optimale lambdawaarde.

We kunnen de volgende code gebruiken om de coëfficiëntschattingen voor dit model te verkrijgen:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

Er wordt geen coëfficiënt weergegeven voor de drat- voorspeller omdat lasso-regressie de coëfficiënt tot nul heeft teruggebracht. Dit betekent dat hij volledig uit het model werd verwijderd omdat hij niet genoeg invloed had.

Merk op dat dit een belangrijk verschil is tussen ridge-regressie en lasso-regressie . Ridge-regressie reduceert alle coëfficiënten naar nul, maar lasso-regressie heeft het potentieel om voorspellers uit het model te verwijderen door de coëfficiënten volledig tot nul terug te brengen.

We kunnen het uiteindelijke lasso-regressiemodel ook gebruiken om voorspellingen te doen over nieuwe waarnemingen. Stel dat we een nieuwe auto hebben met de volgende kenmerken:

• mpg: 24
• gewicht: 2,5
• prijs: 3,5
• qsec: 18,5

De volgende code laat zien hoe u het gepaste lasso-regressiemodel kunt gebruiken om de pk- waarde van deze nieuwe waarneming te voorspellen:

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

Op basis van de ingevoerde waarden voorspelt het model dat deze auto een pk- waarde van 109,0842 zal hebben.

Ten slotte kunnen we de R-kwadraat van het model berekenen op basis van de trainingsgegevens:

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

Het R-kwadraat blijkt 0,8047064 te zijn. Dat wil zeggen dat het beste model 80,47% van de variatie in de responswaarden van de trainingsgegevens kon verklaren.

De volledige R-code die in dit voorbeeld wordt gebruikt, vindt u hier .