Wat is latijnse hypercube-sampling?

Latin hypercube sampling is een methode die gebruikt kan worden om willekeurige getallen te bemonsteren waarbij de monsters uniform verdeeld zijn over een monsterruimte.

Het wordt veel gebruikt om steekproeven te genereren, de zogenaamde gecontroleerde willekeurige steekproeven , en wordt vaak toegepast bij Monte Carlo-analyses omdat het het aantal simulaties dat nodig is om nauwkeurige resultaten te verkrijgen aanzienlijk kan verminderen.

Voorbeeld introductie

Om het idee van Latijnse hypercube-sampling te begrijpen, overweeg het volgende eenvoudige voorbeeld:

Stel dat we een steekproef van 2 waarden willen verkrijgen uit een normaal verdeelde dataset met een gemiddelde van 0 en een standaarddeviatie van 1.

Als we een echte willekeurige getallengenerator hebben gebruikt om dit voorbeeld te verkrijgen, is het mogelijk dat beide waarden groter zijn dan 0 of dat beide waarden kleiner zijn dan 0.

Als we echter Latijnse hypercube-sampling zouden gebruiken om dit monster te verkrijgen, zou het gegarandeerd zijn dat de ene waarde groter dan 0 zou zijn en de andere kleiner dan 0, omdat we de monsterruimte specifiek zouden kunnen verdelen in een gebied met waarden groter dan 0 en een regio met waarden kleiner dan 0, selecteer vervolgens een willekeurige steekproef uit elke regio.

Eendimensionale Latijnse hypercube-sampling

Het idee achter eendimensionale Latijnse hypercube-steekproef is eenvoudig: verdeel een gegeven CDF in n verschillende regio’s en kies willekeurig een waarde in elke regio om een steekproef met grootte n te verkrijgen.

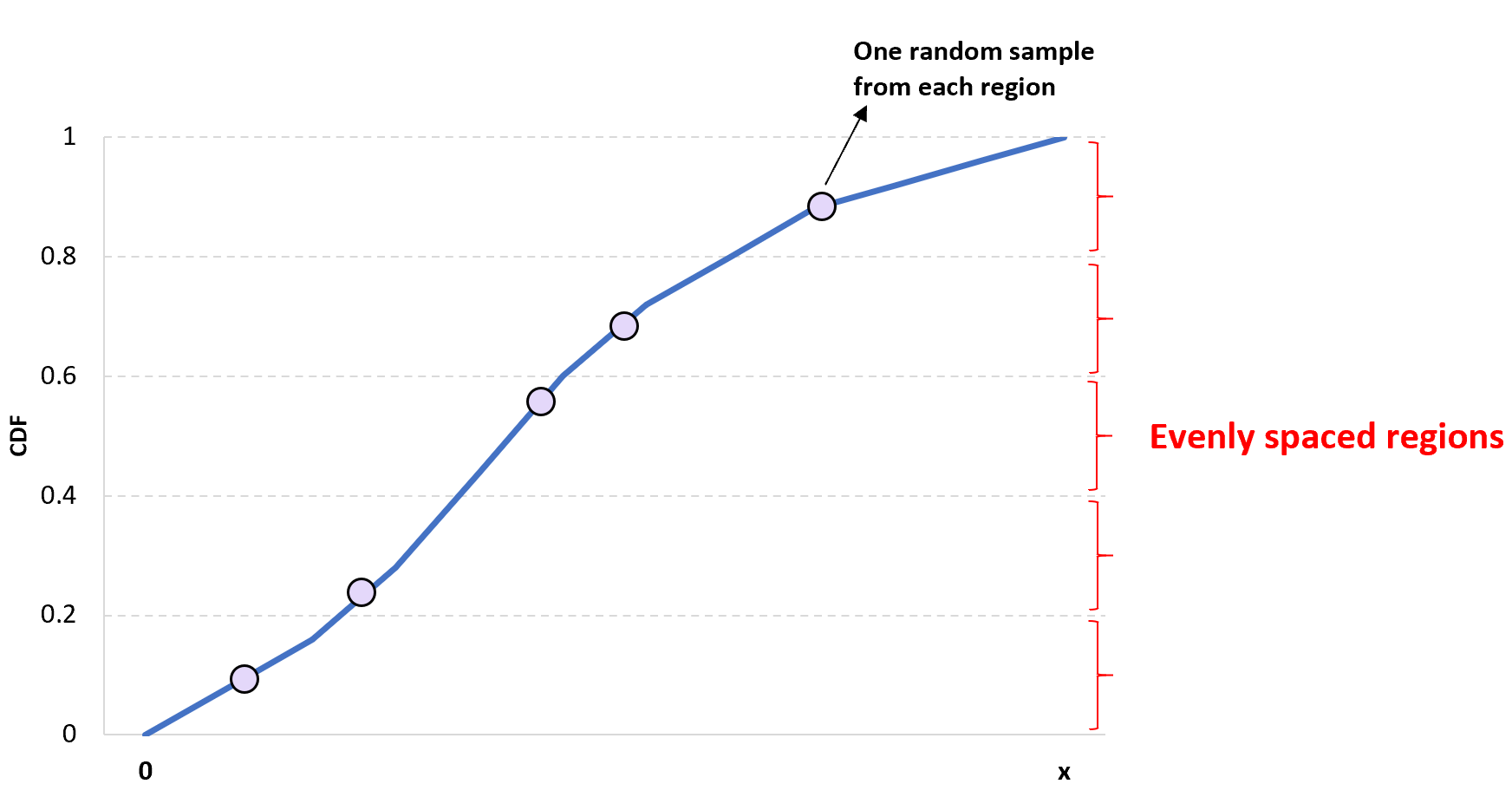
Het voordeel van deze aanpak is dat deze ervoor zorgt dat ten minste één waarde uit elke regio in de steekproef wordt opgenomen.

Bemonstering van tweedimensionale Latijnse hyperkubussen

We kunnen het idee van eendimensionale Latijnse hypercube-sampling ook gemakkelijk uitbreiden naar twee dimensies.

Voor twee variabelen, x en y, kunnen we de steekproefruimte van elke variabele verdelen in n gelijkmatig verdeelde gebieden en een willekeurige steekproef uit elke steekproefruimte selecteren om willekeurige waarden op twee dimensies te verkrijgen.

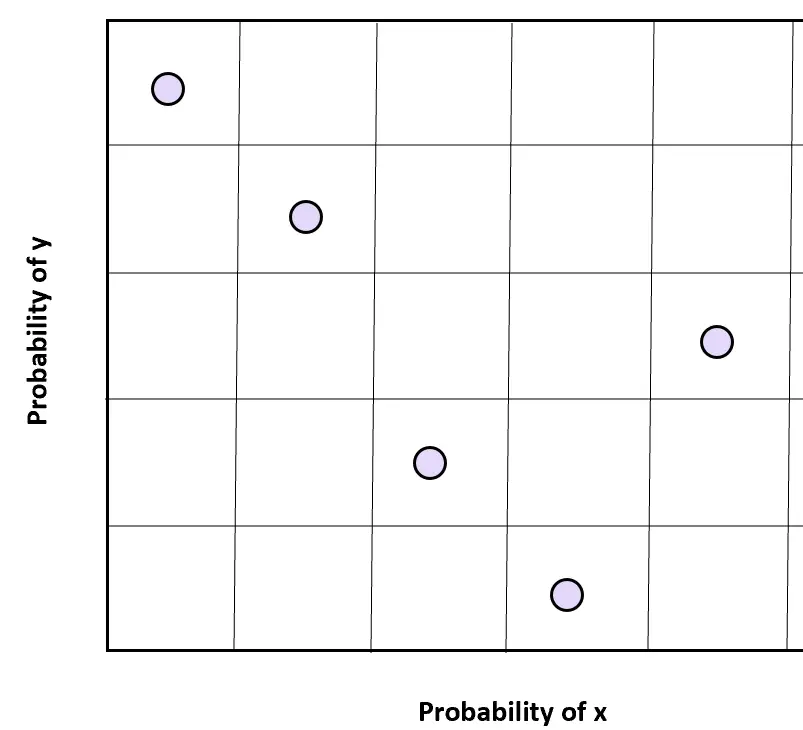
Het is belangrijk op te merken dat de twee variabelen onafhankelijk moeten zijn om met deze bemonsteringstechniek de gewenste resultaten te bereiken.

N-dimensionale Latijnse hyperkubusbemonstering

Om Latijnse hypercube-sampling in grotere dimensies uit te voeren, kunnen we het idee van tweedimensionale Latijnse hypercube-sampling eenvoudigweg uitbreiden naar nog meer dimensies.

Elke variabele wordt eenvoudigweg verdeeld in gelijkmatig verdeelde gebieden en willekeurige steekproeven worden vervolgens uit elke regio gekozen om een gecontroleerde willekeurige steekproef te verkrijgen.

Gerelateerd: Wat zijn hoogdimensionale gegevens?

Waarom Latin Hypercube-sampling gebruiken?

Het belangrijkste voordeel van Latijnse hypercube-steekproeven is dat er steekproeven worden geproduceerd die de werkelijke onderliggende verdeling weerspiegelen en dat er vaak veel kleinere steekproeven nodig zijn dan bij eenvoudige willekeurige steekproeven .

Deze steekproefmethode kan met name nuttig zijn als u werkt met gegevens met een groot aantal dimensies en willekeurige steekproeven moet verkrijgen die zeker de werkelijke onderliggende distributie van de gegevens weerspiegelen.