Hoe de variantie-inflatiefactor (vif) in sas te berekenen

Bij regressieanalyse treedt multicollineariteit op wanneer twee of meer voorspellende variabelen sterk met elkaar gecorreleerd zijn, zodat ze geen unieke of onafhankelijke informatie verschaffen in het regressiemodel.

Als de mate van correlatie tussen variabelen hoog genoeg is, kan dit problemen veroorzaken bij het aanpassen en interpreteren van het regressiemodel.

Eén manier om multicollineariteit te detecteren is door een metriek te gebruiken die bekend staat als de variantie-inflatiefactor (VIF) , die de correlatie en sterkte van de correlatie tussen verklarende variabelen in een regressiemodel meet.

In deze zelfstudie wordt uitgelegd hoe u VIF in SAS berekent.

Voorbeeld: VIF berekenen in SAS

Voor dit voorbeeld maken we een gegevensset die de kenmerken van 10 basketbalspelers beschrijft:

 /*create dataset*/
data my_data;
    input rating points assists rebounds;
    datalines ;
90 25 5 11
85 20 7 8
82 14 7 10
88 16 8 6
94 27 5 6
90 20 7 9
76 12 6 6
75 15 9 10
87 14 9 10
86 19 5 7
;
run ;

/*view dataset*/
proc print data =my_data; 

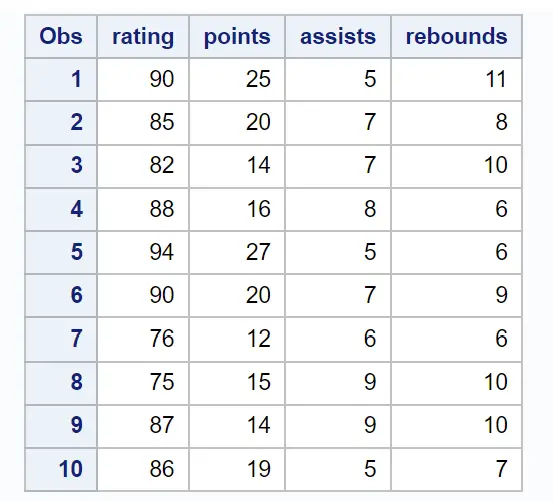
Laten we zeggen dat we een meervoudig lineair regressiemodel willen passen met behulp van scoring als de responsvariabele en points , assists en rebounds als de voorspellende variabelen.

We kunnen PROC REG gebruiken om dit regressiemodel uit te rusten met de VIF- optie om VIF-waarden te berekenen voor elke voorspellende variabele in het model:

 /*fit regression model and calculate VIF values*/
proc reg data =my_data;
    model rating = points assists rebounds / lively ;
run ; 

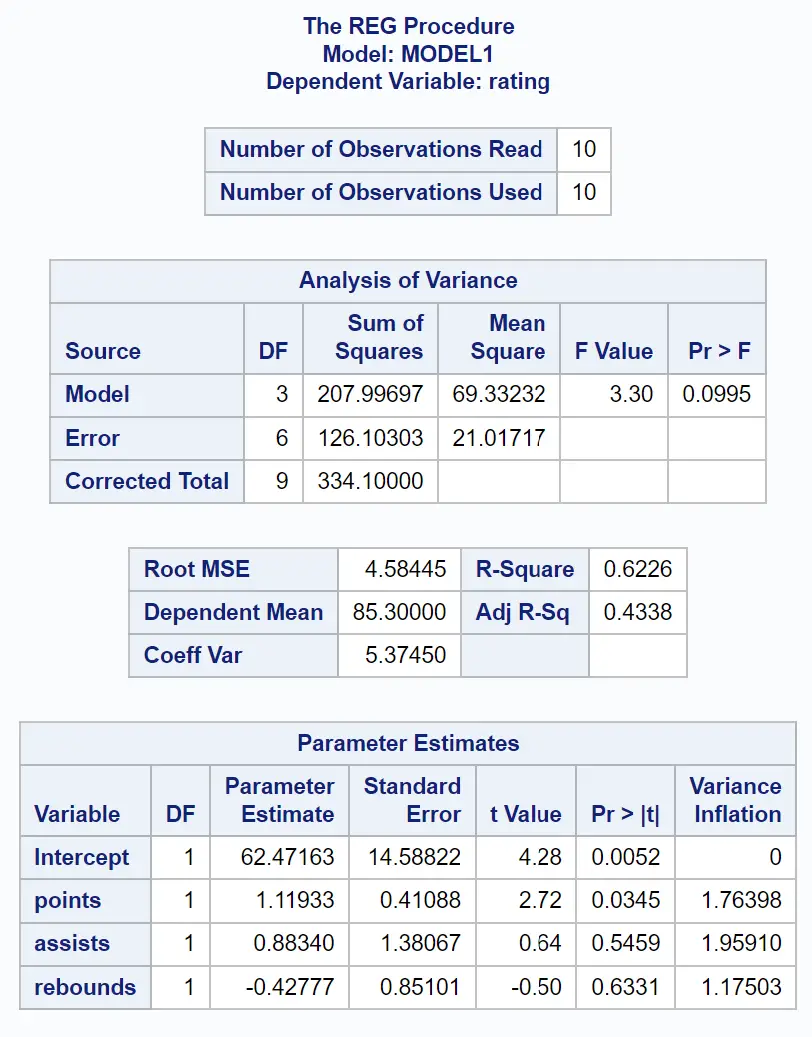
Uit de tabel Parameterschattingen kunnen we de VIF-waarden voor elk van de voorspellende variabelen zien:

• punten: 1,76398
• assists: 1.96591
• rebounds: 1,17503

Opmerking: Negeer de VIF voor “Intercept” in de sjabloon, aangezien deze waarde niet relevant is.

De VIF-waarde begint bij 1 en heeft geen bovengrens. Een algemene regel voor het interpreteren van VIF’s is:

• Een waarde van 1 geeft aan dat er geen correlatie bestaat tussen een bepaalde voorspellende variabele en enige andere voorspellende variabele in het model.
• Een waarde tussen 1 en 5 duidt op een gematigde correlatie tussen een bepaalde voorspellende variabele en andere voorspellende variabelen in het model, maar deze is vaak niet ernstig genoeg om speciale aandacht te vereisen.
• Een waarde groter dan 5 duidt op een potentieel ernstige correlatie tussen een bepaalde voorspellende variabele en andere voorspellende variabelen in het model. In dit geval zijn de coëfficiëntschattingen en p-waarden in de regressieresultaten waarschijnlijk onbetrouwbaar.

Omdat elk van de VIF-waarden van de voorspellende variabelen in ons regressiemodel dichtbij 1 ligt, is multicollineariteit in ons voorbeeld geen probleem.

Hoe om te gaan met multicollineariteit

Als u vaststelt dat multicollineariteit een probleem is in uw regressiemodel, zijn er verschillende veelgebruikte manieren om dit op te lossen:

1. Verwijder een of meer van de sterk gecorreleerde variabelen.

Dit is in de meeste gevallen de snelste oplossing en is vaak een acceptabele oplossing omdat de variabelen die u verwijdert sowieso overbodig zijn en weinig unieke of onafhankelijke informatie aan het model toevoegen.

2. Combineert de voorspellende variabelen op een bepaalde manier lineair, bijvoorbeeld door ze op een of andere manier toe te voegen of af te trekken.

Door dit te doen, kunt u een nieuwe variabele maken die de informatie van beide variabelen omvat en heeft u niet langer een multicollineariteitsprobleem.

3. Voer een analyse uit die is ontworpen om rekening te houden met sterk gecorreleerde variabelen, zoals hoofdcomponentenanalyse of PLS-regressie (partiële kleinste kwadraten).

Deze technieken zijn specifiek ontworpen om sterk gecorreleerde voorspellende variabelen te verwerken.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe u een restplot in SAS maakt
Hoe de kookafstand in SAS te berekenen