Hoe u de levene-test uitvoert in spss

Levene’s test wordt gebruikt om te bepalen of twee of meer groepen gelijke varianties hebben.

Het wordt veel gebruikt omdat veel statistische tests berusten op de aanname dat groepen gelijke varianties hebben.

In deze tutorial wordt uitgelegd hoe u de Levene-test uitvoert in SPSS.

Voorbeeld: Levene-test in SPSS

Onderzoekers willen weten of drie verschillende meststoffen tot verschillende niveaus van plantengroei leiden.

Ze selecteren willekeurig 30 verschillende planten en verdelen ze in drie groepen van 10, waarbij elke groep een andere meststof wordt toegediend. Na een maand meten ze de hoogte van elke plant.

De volgende schermafbeelding toont de hoeveelheid groei (in inches) voor elke individuele plant, samen met de meststof (1, 2 of 3) die op de plant is aangebracht:

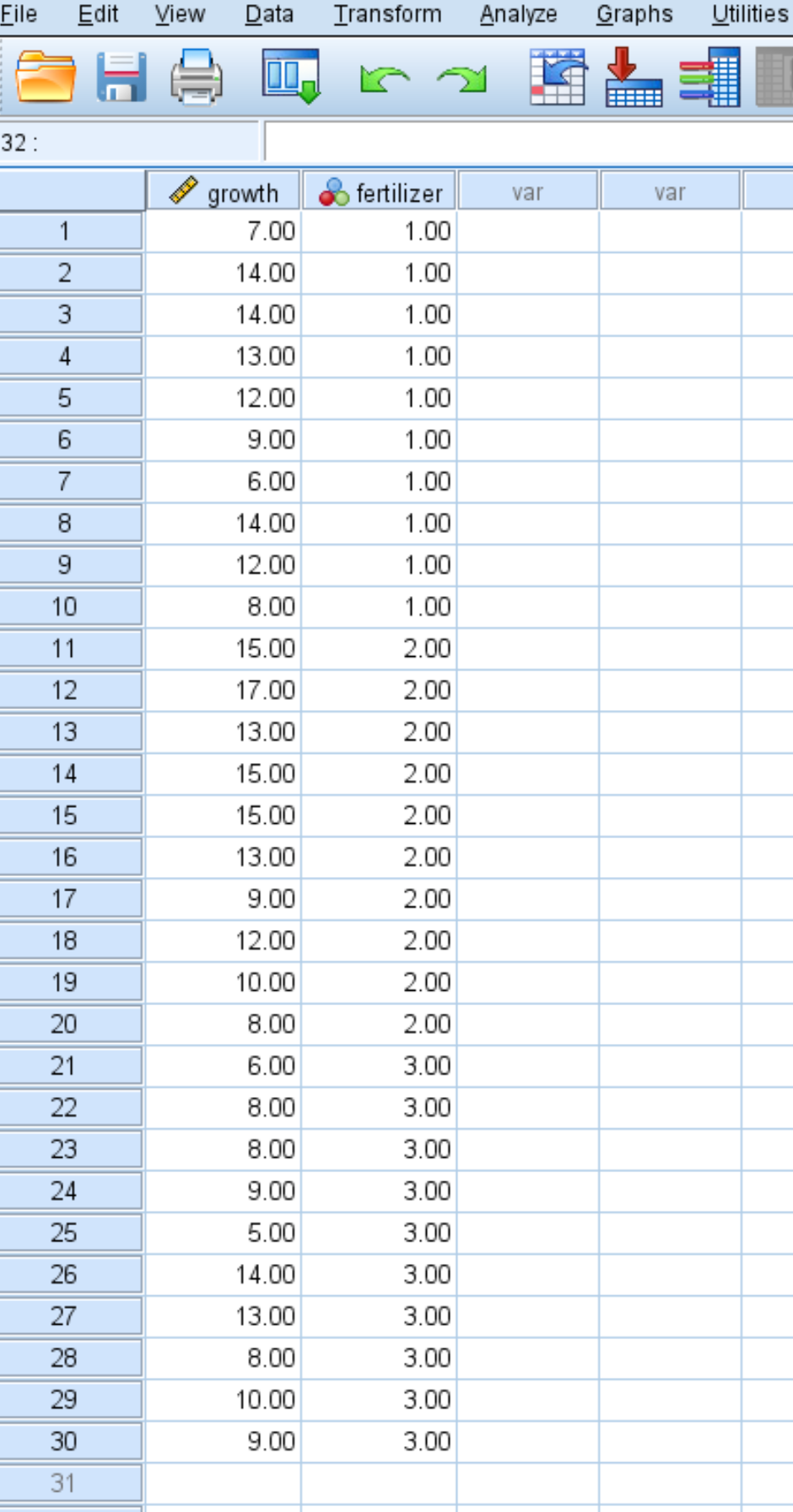
Volg de volgende stappen om Levene’s test in SPSS uit te voeren om te bepalen of de drie groepen al dan niet gelijke varianties hebben.

Stap 1: Kies de optie Ontdekken.

Klik op het tabblad Analyseren , vervolgens op Beschrijvende statistieken en vervolgens op Verkennen :

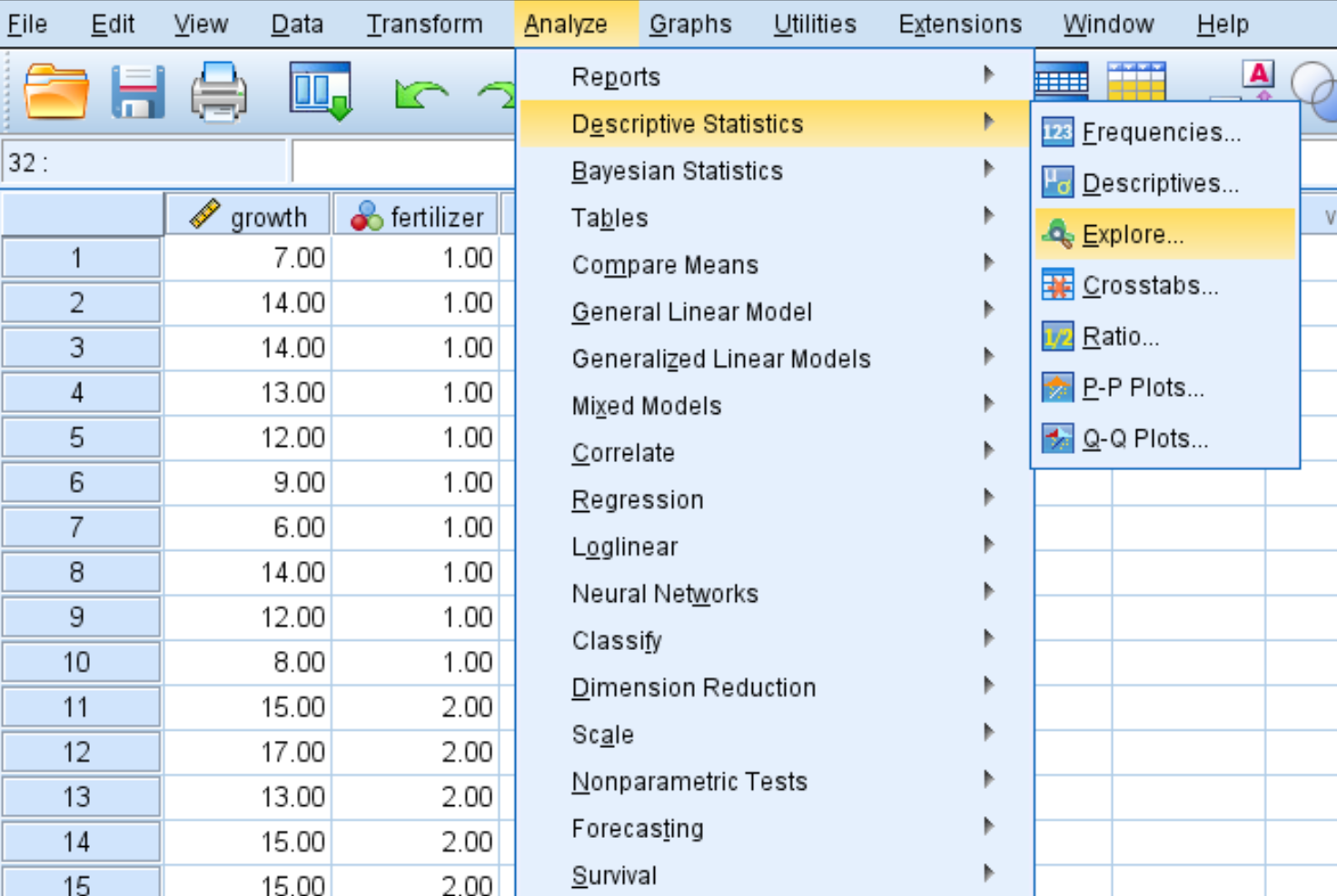
Stap 2: Vul de benodigde waarden in om de test uit te voeren.

Sleep groei naar het vak onder Afhankelijke lijst en sleep bemesten   in het vak onder Lijst met factoren.

Klik vervolgens op Plots en zorg ervoor dat Power Estimation is geselecteerd. Klik vervolgens op doorgaan . Klik vervolgens op OK .

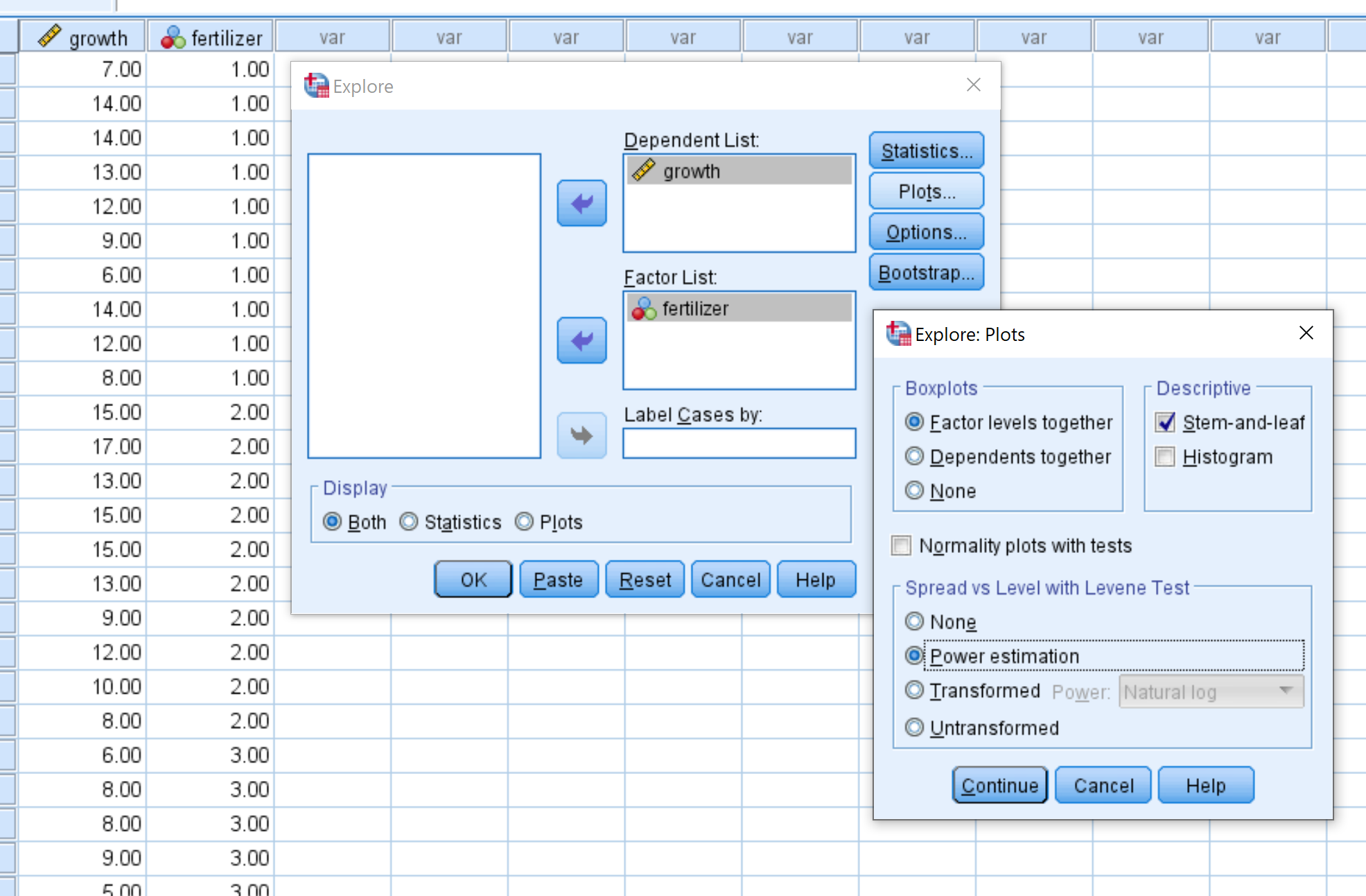
Stap 3: Interpreteer de resultaten.

Zodra u op OK klikt, worden de Levene-testresultaten weergegeven:

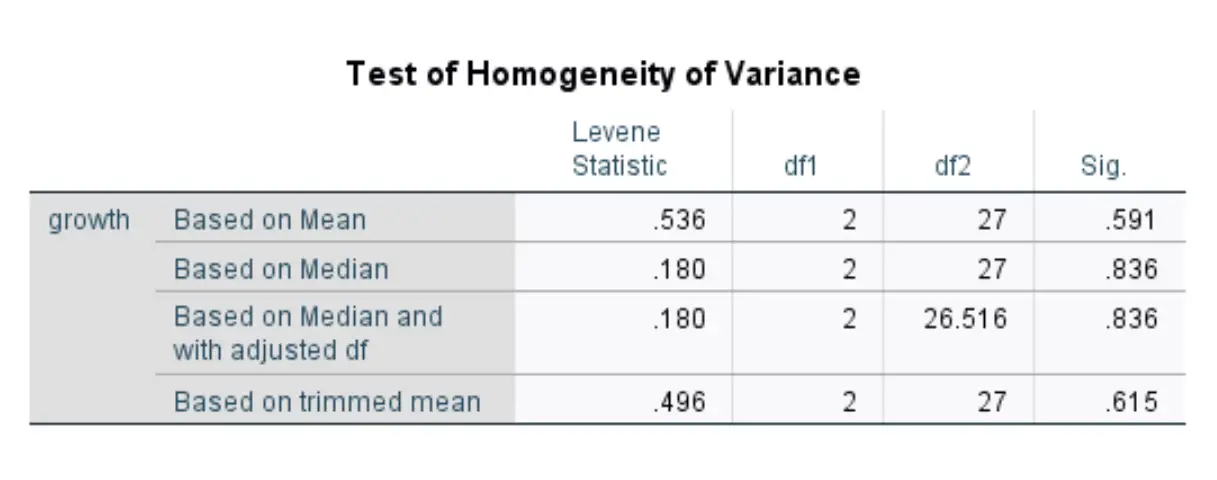
Deze tabel toont teststatistieken voor vier verschillende versies van de Levene-test. De getallen waarin we geïnteresseerd zijn, staan in de eerste rij, die de resultaten van de Levene-test weergeeft op basis van het gemiddelde.

De teststatistiek is 0,536 en de overeenkomstige p-waarde is 0,591* .

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we niet voldoende bewijs hebben om te zeggen dat de variantie in plantengroei tussen de drie meststoffen significant verschillend is.

Met andere woorden: de drie groepen hebben gelijke varianties. Als we een statistische test zouden uitvoeren (zoals een eenrichtings-ANOVA ) die ervan uitgaat dat elke groep een gelijke variantie heeft, dan zou aan deze veronderstelling worden voldaan.

* Deze p-waarde komt overeen met een F-statistiek van 0,536 met teller df = 2 en noemer df = 27. Deze p-waarde kan ook worden berekend met de F-verdelingscalculator.