Inleiding tot eenvoudige lineaire regressie

Eenvoudige lineaire regressie is een statistische methode die u kunt gebruiken om de relatie tussen twee variabelen, x en y, te begrijpen.

Een variabele, x , staat bekend als een voorspellende variabele .

De andere variabele, y , staat bekend als de responsvariabele .

Stel dat we bijvoorbeeld de volgende gegevensset hebben met het gewicht en de lengte van zeven individuen:

Laat gewicht de voorspellende variabele zijn en laat lengte de responsvariabele zijn.

Als we deze twee variabelen grafisch weergeven met behulp van een spreidingsdiagram, met het gewicht op de x-as en de hoogte op de y-as, ziet het er zo uit:

Stel dat we de relatie tussen gewicht en lengte willen begrijpen. Uit het spreidingsdiagram kunnen we duidelijk zien dat naarmate het gewicht toeneemt, de lengte ook de neiging heeft toe te nemen, maar om deze relatie tussen gewicht en lengte daadwerkelijk te kwantificeren moeten we lineaire regressie gebruiken.

Met behulp van lineaire regressie kunnen we de lijn vinden die het beste bij onze gegevens past. Deze lijn staat bekend als de regressielijn met de kleinste kwadraten en kan worden gebruikt om ons te helpen de relaties tussen gewicht en lengte te begrijpen.

Meestal gebruikt u software zoals Microsoft Excel, SPSS of een grafische rekenmachine om de vergelijking voor deze lijn te vinden.

De formule voor de lijn met de beste pasvorm is geschreven:

ŷ = _b0 + _b1 x

waarbij ŷ de voorspelde waarde van de responsvariabele is, b ₀ het snijpunt is, b ₁ de regressiecoëfficiënt is en x de waarde van de voorspellende variabele is.

Gerelateerd: 4 voorbeelden van het gebruik van lineaire regressie in het echte leven

Vind de “meest geschikte lijn”

Voor dit voorbeeld kunnen we eenvoudigweg onze gegevens in de statistische lineaire regressiecalculator pluggen en op Berekenen drukken:

De rekenmachine vindt automatisch de regressielijn met de kleinste kwadraten :

ŷ = 32,7830 + 0,2001x

Als we uitzoomen op ons vorige spreidingsdiagram en deze lijn aan de grafiek toevoegen, ziet het er zo uit:

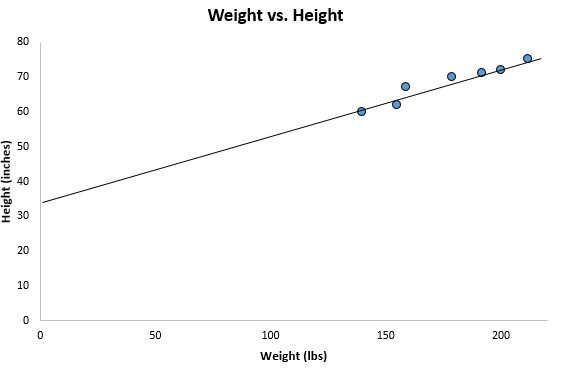
Merk op hoe onze gegevenspunten nauw verspreid zijn rond deze lijn. Deze regressielijn met de kleinste kwadraten is inderdaad de lijn die het meest geschikt is voor onze gegevens tussen alle mogelijke lijnen die we zouden kunnen tekenen.

Hoe een regressielijn met de kleinste kwadraten te interpreteren

Hier leest u hoe u deze regressielijn met de kleinste kwadraten interpreteert: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Dit betekent dat wanneer het variabele gewicht van de voorspeller nul pond is, de voorspelde lengte 32,7830 inch is. Soms kan het nuttig zijn om de waarde van b ₀ te weten, maar in dit specifieke voorbeeld heeft het geen zin om b ₀ te interpreteren, aangezien een persoon geen nul pond kan wegen.

_b1 = 0,2001 . Dit betekent dat een toename van één eenheid in x gepaard gaat met een toename van 0,2001 eenheid in y . In dit geval gaat een gewichtstoename van één pond gepaard met een toename van de lengte van 0,2001 inch.

Hoe de regressielijn met de kleinste kwadraten te gebruiken

Met behulp van deze regressielijn met de kleinste kwadraten kunnen we vragen beantwoorden zoals:

Hoe lang moeten we verwachten van iemand die 170 pond weegt?

Om deze vraag te beantwoorden, kunnen we eenvoudigweg 170 in onze regressielijn voor x invoegen en voor y oplossen:

ŷ = 32,7830 + 0,2001(170) = 66,8 inch

Hoe lang moeten we verwachten van iemand die 150 pond weegt?

Om deze vraag te beantwoorden, kunnen we 150 in onze regressielijn voor x invoegen en voor y oplossen:

ŷ = 32,7830 + 0,2001(150) = 62,798 inch

Let op: Wanneer u een regressievergelijking gebruikt om vragen als deze te beantwoorden, zorg er dan voor dat u voor de voorspellende variabele alleen waarden gebruikt die binnen het bereik van de voorspellende variabele in de dataset liggen. oorsprong die we hebben gebruikt om de regressielijn met de kleinste kwadraten te genereren. De gewichten in onze dataset varieerden bijvoorbeeld tussen 140 en 212 pond. Het is dus logisch om vragen over de verwachte lengte te beantwoorden als het gewicht tussen de 140 en 212 pond ligt.

De determinatiecoëfficiënt

Eén manier om te meten hoe goed de regressielijn met de kleinste kwadraten bij de gegevens past, is door de determinatiecoëfficiënt te gebruiken, genaamd R ² .

De determinatiecoëfficiënt is het deel van de variantie in de responsvariabele dat kan worden verklaard door de voorspellende variabele.

De determinatiecoëfficiënt kan variëren van 0 tot 1. Een waarde van 0 geeft aan dat de responsvariabele helemaal niet kan worden verklaard door de voorspellende variabele. Een waarde van 1 geeft aan dat de responsvariabele perfect en zonder fouten kan worden verklaard door de voorspellende variabele.

Een R ² tussen 0 en 1 geeft aan in hoeverre de responsvariabele verklaard kan worden door de voorspellende variabele. Een ^R2 van 0,2 geeft bijvoorbeeld aan dat 20% van de variantie in de responsvariabele kan worden verklaard door de voorspellende variabele; een R ² van 0,77 geeft aan dat 77% van de variantie in de responsvariabele kan worden verklaard door de voorspellende variabele.

Merk op dat we in ons vorige resultaat een R ² van 0,9311 hebben verkregen, wat aangeeft dat 93,11% van de variabiliteit in lengte kan worden verklaard door de gewichtsvoorspellende variabele:

Dit vertelt ons dat gewicht een zeer goede indicator is voor de lengte.

Lineaire regressieaannames

Om de resultaten van een lineair regressiemodel geldig en betrouwbaar te laten zijn, moeten we verifiëren dat aan de volgende vier aannames wordt voldaan:

1. Lineaire relatie: Er bestaat een lineaire relatie tussen de onafhankelijke variabele, x, en de afhankelijke variabele, y.

2. Onafhankelijkheid: De residuen zijn onafhankelijk. In het bijzonder is er geen correlatie tussen opeenvolgende residuen in tijdreeksgegevens.

3. Homoscedasticiteit: de residuen hebben een constante variantie op elk niveau van x.

4. Normaliteit: De modelresiduen zijn normaal verdeeld.

Als aan een of meer van deze aannames niet wordt voldaan, kunnen de resultaten van onze lineaire regressie onbetrouwbaar of zelfs misleidend zijn.

Raadpleeg dit artikel voor een uitleg van elke aanname, hoe u kunt bepalen of aan de aanname wordt voldaan en wat u moet doen als niet aan de aanname wordt voldaan.