Lineaire regressie uitvoeren in google spreadsheets

Lineaire regressie is een methode die kan worden gebruikt om de relatie tussen een of meer verklarende variabelen en een responsvariabele te kwantificeren.

We gebruiken eenvoudige lineaire regressie als er slechts één verklarende variabele is en meervoudige lineaire regressie als er twee of meer verklarende variabelen zijn.

Beide typen regressies kunnen worden uitgevoerd met de functie LIJNSCH() van Google Spreadsheets, die de volgende syntaxis gebruikt:

LIJNSCH (bekende_data_y, bekende_data_x, berekenen_b, uitgebreid)

Goud:

• bekende_data_y: reeks antwoordwaarden
• bekende_data_x: Tabel met verklarende waarden
• berekenen_b: geeft aan of het snijpunt al dan niet moet worden berekend. Dit is standaard WAAR en we laten het zo voor lineaire regressie.
• uitgebreid: geeft aan of er al dan niet aanvullende regressiestatistieken moeten worden verstrekt die verder gaan dan alleen de helling en het snijpunt. Dit is standaard ONWAAR, maar we zullen in onze voorbeelden specificeren dat dit WAAR is.

De volgende voorbeelden laten zien hoe u deze functie in de praktijk kunt gebruiken.

Eenvoudige lineaire regressie in Google Spreadsheets

Stel dat we inzicht willen krijgen in de relatie tussen gestudeerde uren en examenresultaten. studeren voor een examen en het cijfer dat op het examen is behaald.

Om deze relatie te onderzoeken, kunnen we een eenvoudige lineaire regressie uitvoeren met bestudeerde uren als verklarende variabele en examenscores als responsvariabele.

De volgende schermafbeelding laat zien hoe u een eenvoudige lineaire regressie kunt uitvoeren met behulp van een gegevensset van 20 leerlingen, waarbij de volgende formule wordt gebruikt in cel D2:

= LIJN ( B2:B21 , A2:A21 , WAAR , WAAR )

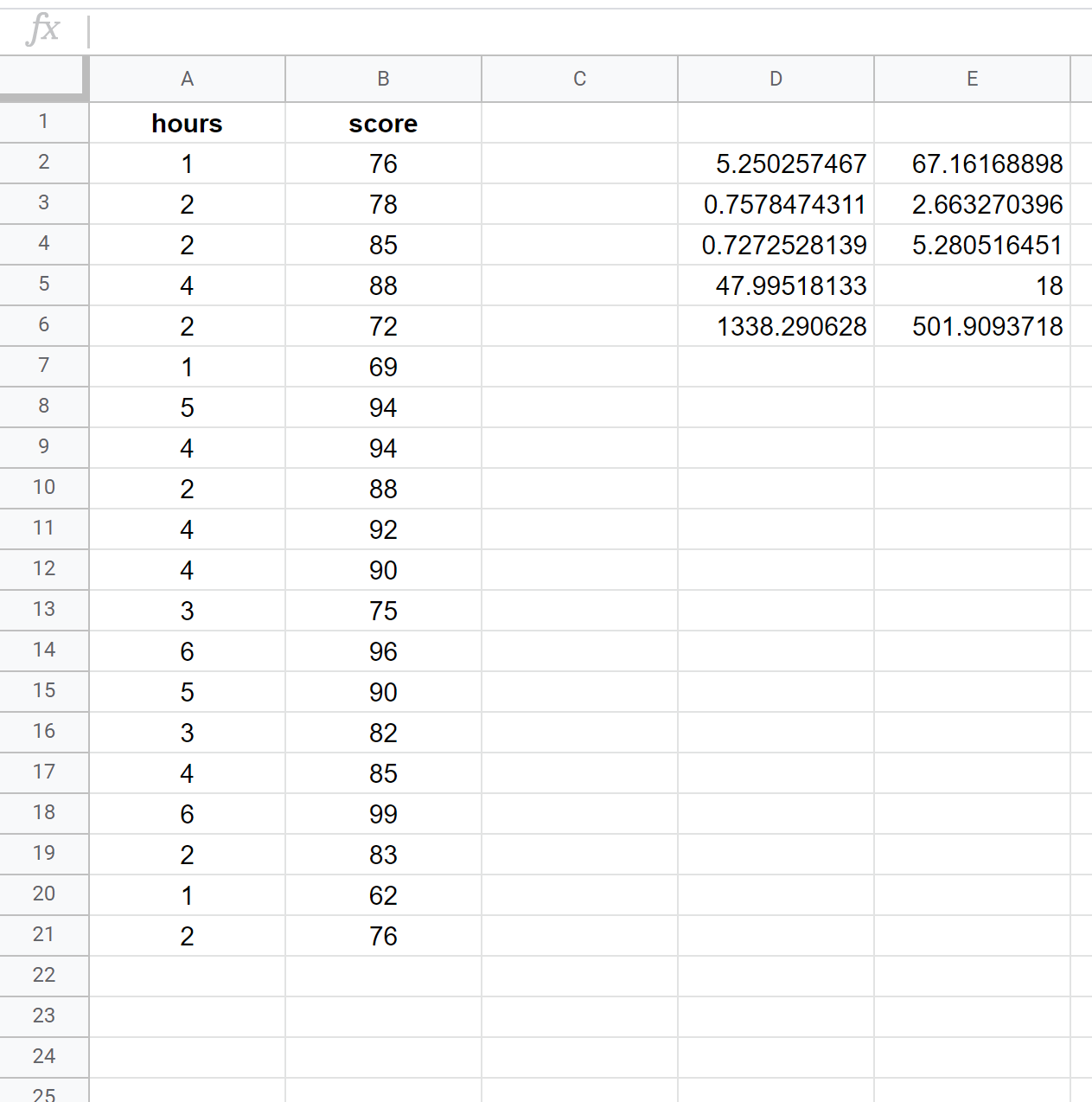
De volgende schermafbeelding biedt annotaties voor de uitvoer:

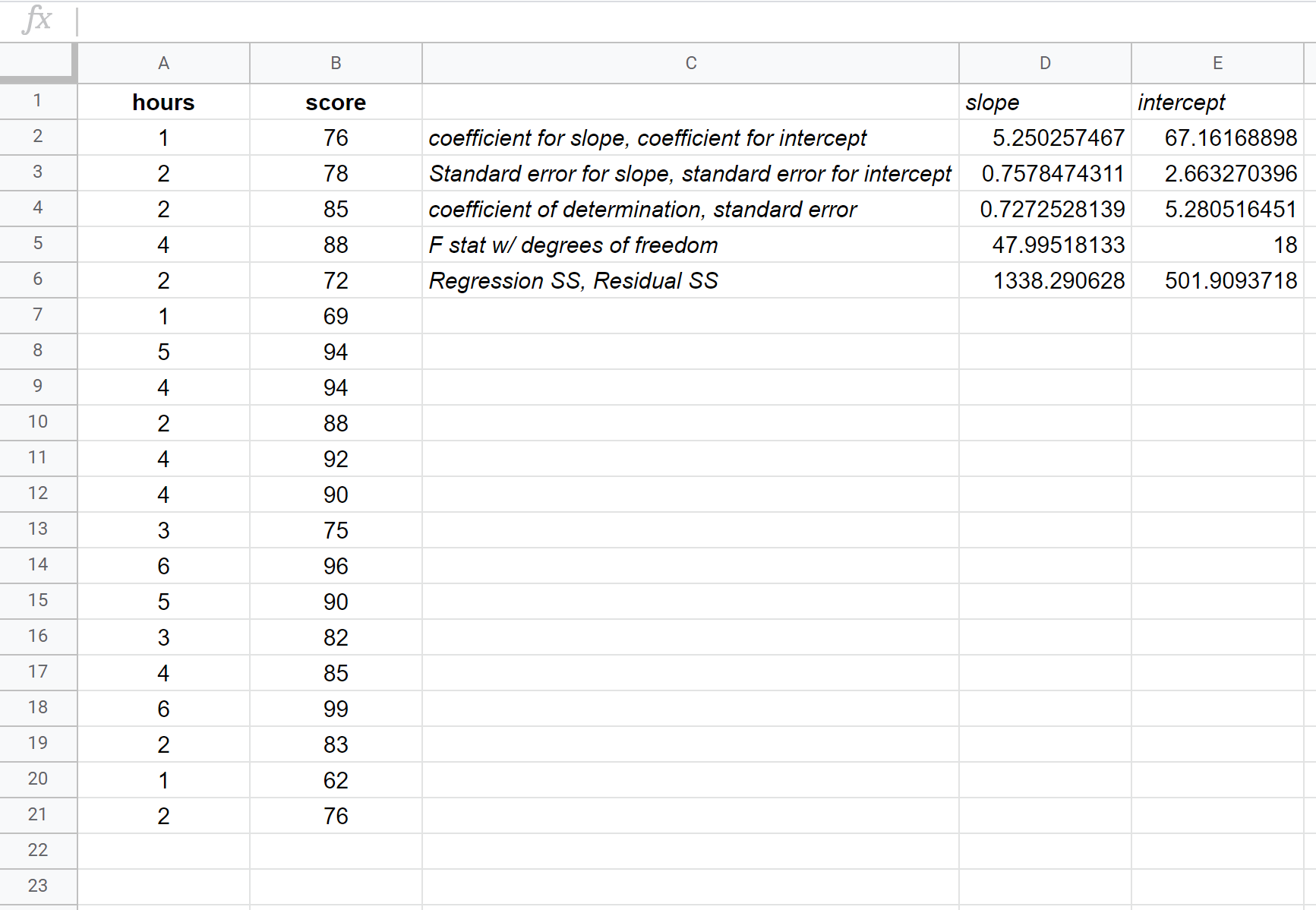
Zo interpreteert u de meest relevante cijfers in het resultaat:

R Vierkant: 0,72725 . Dit wordt de determinatiecoëfficiënt genoemd. Het is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabele. In dit voorbeeld kan ongeveer 72,73% van de variatie in examenscores worden verklaard door het aantal gestudeerde uren.

Standaardfout: 5.2805 . Dit is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. In dit voorbeeld wijken de waargenomen waarden gemiddeld 5,2805 eenheden af van de regressielijn.

Coëfficiënten: De coëfficiënten geven ons de getallen die nodig zijn om de geschatte regressievergelijking te schrijven. In dit voorbeeld is de geschatte regressievergelijking:

Examenscore = 67,16 + 5,2503*(uren)

We interpreteren de urencoëfficiënt zo dat voor elk extra bestudeerd uur de examenscore gemiddeld met 5,2503 zou moeten stijgen. We interpreteren de coëfficiënt van het intercept zo dat de verwachte examenscore voor een student die nul uur studeert 67,16 is.

Met deze geschatte regressievergelijking kunnen we de verwachte examenscore voor een student berekenen, op basis van het aantal uren studie. Een student die bijvoorbeeld drie uur studeert, moet een examenscore van 82,91 behalen:

Examenscore = 67,16 + 5,2503*(3) = 82,91

Meerdere lineaire regressie in Google Spreadsheets

Stel dat we willen weten of het aantal uren dat wordt gestudeerd en het aantal afgelegde voorbereidende examens van invloed zijn op het cijfer dat een student krijgt voor een bepaald toelatingsexamen voor de universiteit.

Om deze relatie te onderzoeken, kunnen we een meervoudige lineaire regressie uitvoeren met behulp van bestudeerde uren en voorbereidende examens als verklarende variabelen en examenresultaten als responsvariabele.

De volgende schermafbeelding laat zien hoe u meervoudige lineaire regressie kunt uitvoeren met behulp van een gegevensset van 20 leerlingen, waarbij de volgende formule wordt gebruikt in cel E2:

= RECHTS ( C2:C21 , A2:B21 , WAAR , WAAR )

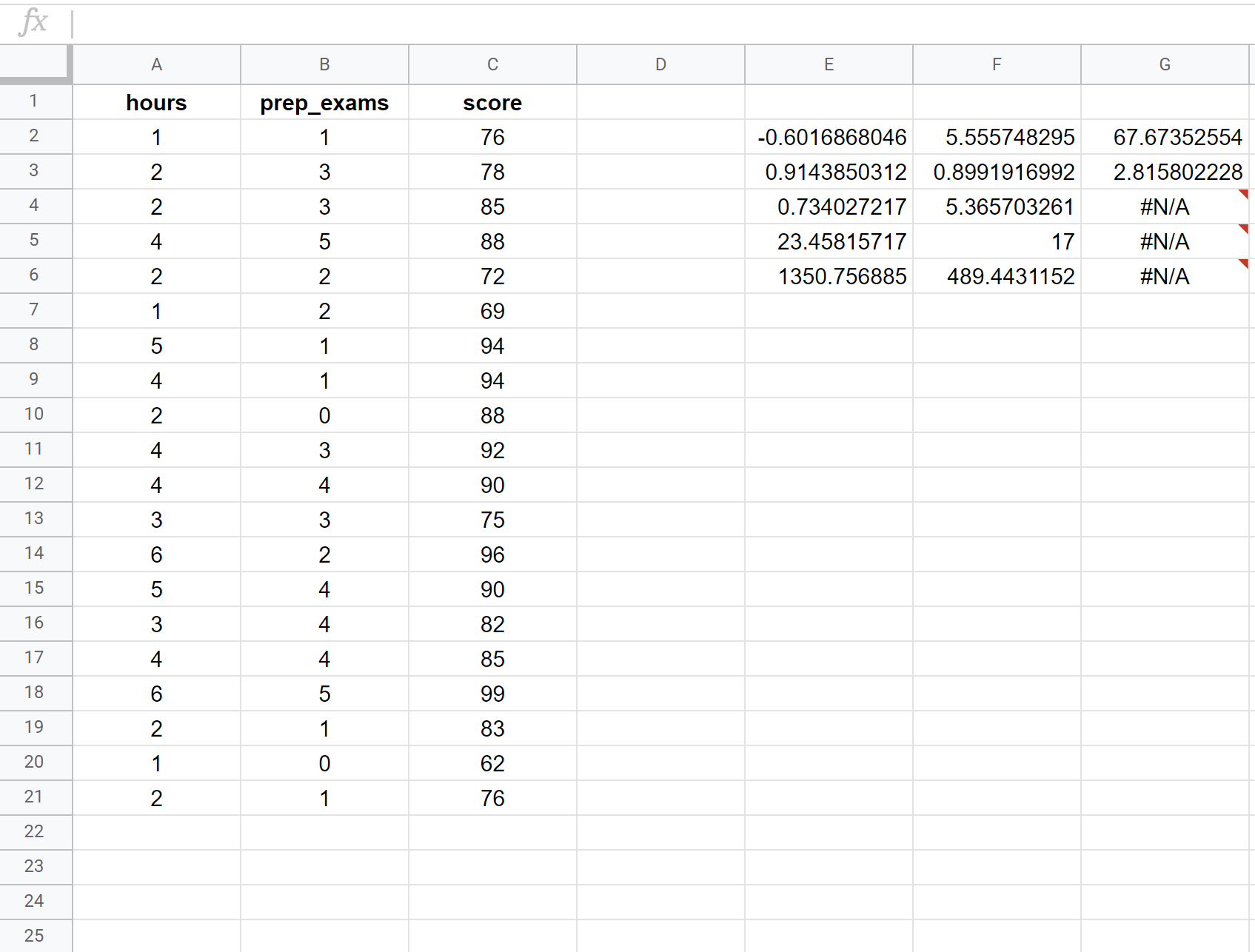
Zo interpreteert u de meest relevante cijfers in het resultaat:

R Kwadraat: 0,734 . Dit wordt de determinatiecoëfficiënt genoemd. Het is het deel van de variantie van de responsvariabele dat kan worden verklaard door de verklarende variabelen. In dit voorbeeld wordt 73,4% van de variatie in examenscores verklaard door het aantal gestudeerde uren en het aantal afgelegde voorbereidende examens.

Standaardfout: 5.3657 . Dit is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. In dit voorbeeld wijken de waargenomen waarden gemiddeld 5,3657 eenheden af van de regressielijn.

Geschatte regressievergelijking: We kunnen de coëfficiënten uit de modeluitvoer gebruiken om de volgende geschatte regressievergelijking te maken:

Examenscore = 67,67 + 5,56*(uren) – 0,60*(voorbereidende examens)

Met deze geschatte regressievergelijking kunnen we de verwachte examenscore voor een student berekenen, op basis van het aantal uren studie en het aantal oefenexamens dat hij/zij aflegt. Een student die bijvoorbeeld drie uur studeert en een voorbereidend examen aflegt, zou een cijfer van 83,75 moeten krijgen:

Examenscore = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in Google Spreadsheets kunt uitvoeren:

Hoe polynomiale regressie uit te voeren in Google Spreadsheets
Hoe u een restplot maakt in Google Spreadsheets