Hoe lineaire regressie uit te voeren op een ti-84-rekenmachine

Lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen een verklarende variabele, x, en een responsvariabele, y, te begrijpen.

In deze tutorial wordt uitgelegd hoe u lineaire regressie uitvoert op een TI-84-rekenmachine.

Voorbeeld: lineaire regressie op een TI-84-rekenmachine

Stel dat we inzicht willen krijgen in de relatie tussen het aantal uren dat een student voor een examen studeert en het cijfer dat hij voor dat examen krijgt.

Om deze relatie te onderzoeken, kunnen we de volgende stappen uitvoeren op een TI-84-rekenmachine om een eenvoudige lineaire regressie uit te voeren met bestudeerde uren als verklarende variabele en examencijfer als responsvariabele.

Stap 1: Voer de gegevens in.

Eerst voeren we de gegevenswaarden in voor de verklarende variabele en de responsvariabele. Druk op Stat en vervolgens op BEWERKEN . Vul in kolom L1 de volgende waarden in voor de verklarende variabele (gestudeerde uren) en in kolom L2 de waarden voor de responsvariabele (examenscore):

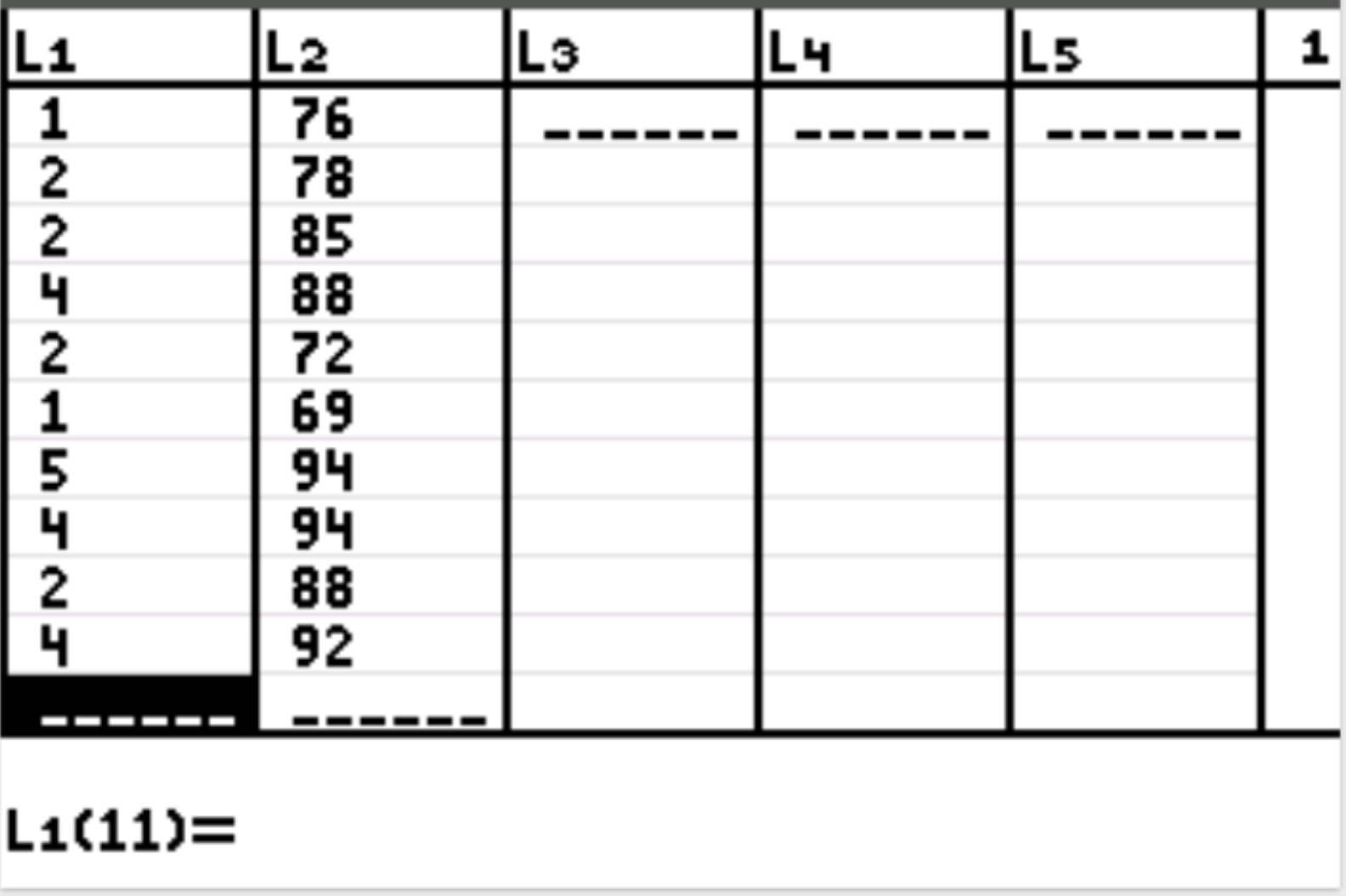
Stap 2: Voer lineaire regressie uit.

Vervolgens zullen we een lineaire regressie uitvoeren. Druk op Stat en scroll vervolgens naar CALC . Scroll vervolgens naar 8: Linreg(a+bx) en druk op Enter .

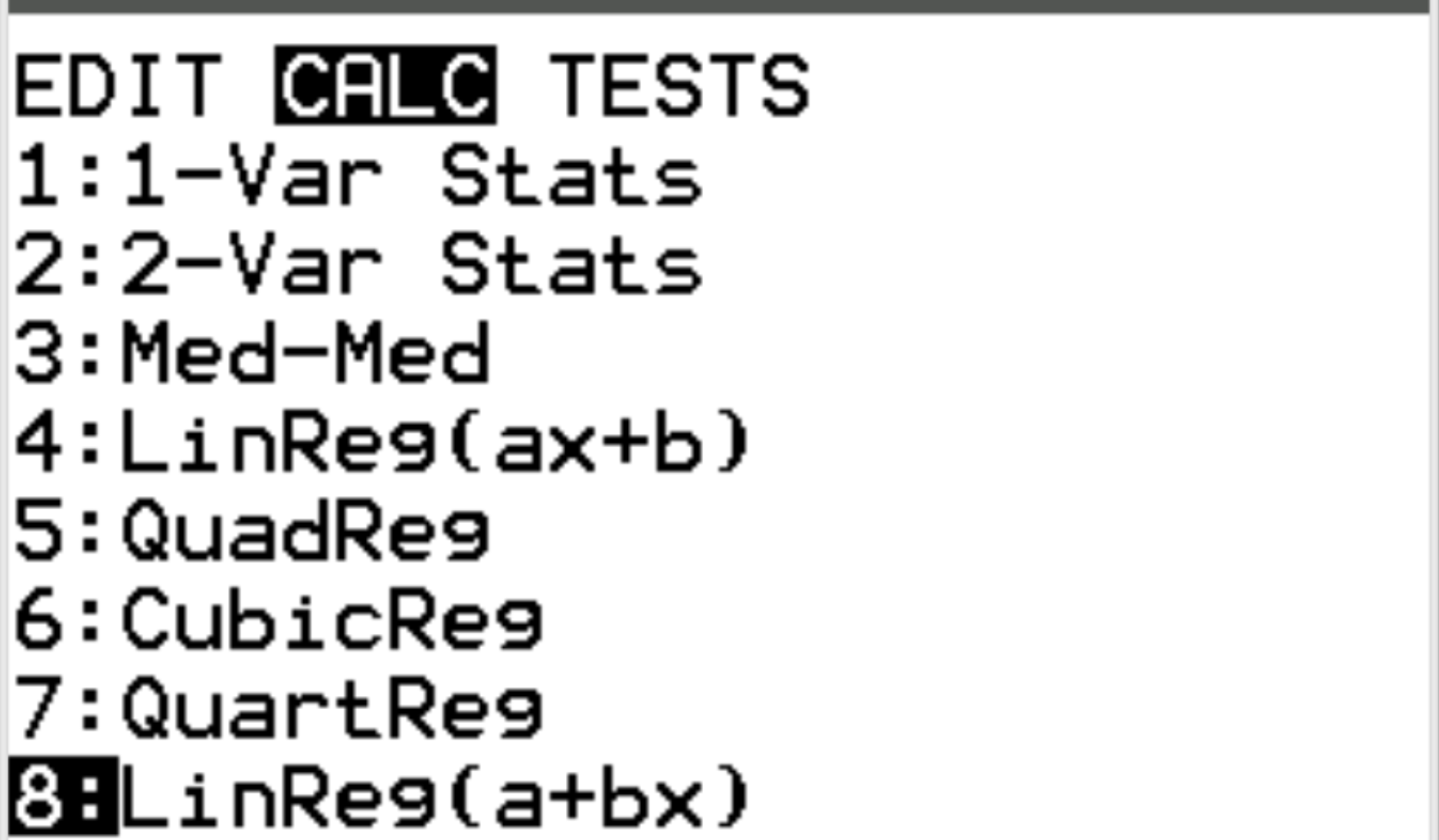
Zorg ervoor dat voor Xlist en Ylist L1 en L2 zijn geselecteerd, aangezien dit de kolommen zijn die we hebben gebruikt om onze gegevens in te voeren. Laat FreqList leeg. Blader omlaag naar Bereken en druk op Enter . De volgende uitvoer verschijnt automatisch:

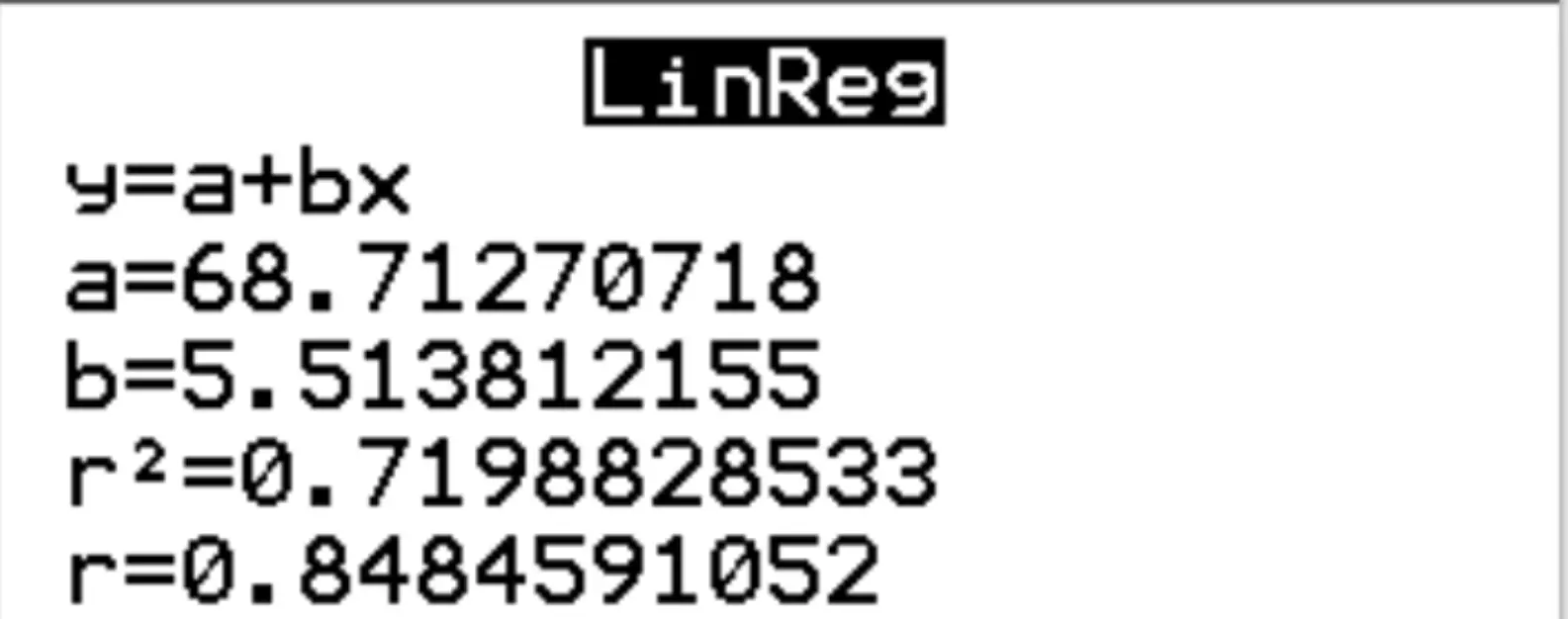
Stap 3: Interpreteer de resultaten.

Uit de resultaten kunnen we zien dat de geschatte regressievergelijking is:

examenscore = 68,7127 + 5,5138*(uren)

We interpreteren de urencoëfficiënt zo dat voor elk extra bestudeerd uur de examenscore gemiddeld met 5,5138 zou moeten stijgen. We interpreteren de coëfficiënt van het intercept zo dat de verwachte examenscore voor een student die nul uur studeert 68,7127 is.

Met deze geschatte regressievergelijking kunnen we de verwachte examenscore voor een student berekenen, op basis van het aantal uren studie.

Een student die bijvoorbeeld drie uur studeert, moet een examenscore van 85,25 behalen:

examenscore = 68,7127 + 5,5138*(3) = 85,25

We kunnen ook zien dat de r kwadraat voor het regressiemodel r ² = 0,7199 is.

Deze waarde staat bekend als de determinatiecoëfficiënt. Het is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabele. In dit voorbeeld kan 71,99% van de variatie in examenscores worden verklaard door het aantal gestudeerde uren.

Aanvullende bronnen

Hoe maak je een resterend plot op een TI-84-rekenmachine?
Hoe kwadratische regressie uit te voeren op een TI-84-rekenmachine
Hoe u exponentiële regressie uitvoert op een TI-84-rekenmachine
Logaritmische regressie uitvoeren op een TI-84-rekenmachine