Hoe de functie lm() in r te gebruiken om lineaire modellen te passen
De functie lm() in R wordt gebruikt om lineaire regressiemodellen aan te passen.
Deze functie gebruikt de volgende basissyntaxis:
lm(formule, gegevens, …)
Goud:
- formule: De lineaire modelformule (bijv. y ~ x1 + x2)
- data: de naam van het datablok dat de gegevens bevat
Het volgende voorbeeld laat zien hoe u deze functie in R kunt gebruiken om het volgende te doen:
- Pas een regressiemodel toe
- Bekijk de samenvatting van de fit van het regressiemodel
- Bekijk modeldiagnostische plots
- Teken het gepaste regressiemodel
- Maak voorspellingen met behulp van het regressiemodel
Pas het regressiemodel aan
De volgende code laat zien hoe u de functie lm() gebruikt om een lineair regressiemodel in R te passen:
#define data df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12), y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22)) #fit linear regression model using 'x' as predictor and 'y' as response variable model <- lm(y ~ x, data=df)
Samenvatting van het regressiemodel weergeven
We kunnen vervolgens de functie summary() gebruiken om de samenvatting van de fit van het regressiemodel weer te geven:
#view summary of regression model
summary(model)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.4793 -0.9772 -0.4772 1.4388 4.6328
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675
Zo interpreteert u de belangrijkste waarden in het model:
- F-statistiek = 18,35, overeenkomstige p-waarde = 0,002675. Omdat deze p-waarde kleiner is dan 0,05 is het model als geheel statistisch significant.
- Meerdere R kwadraat = 0,6964. Dit vertelt ons dat 69,64% van de variatie in de responsvariabele, y, kan worden verklaard door de voorspellende variabele, x.
- Geschatte coëfficiënt van x : 1,2780. Dit vertelt ons dat elke extra eenheidstoename in x gepaard gaat met een gemiddelde toename van 1,2780 in y.
We kunnen vervolgens de coëfficiëntschattingen uit de uitvoer gebruiken om de geschatte regressievergelijking te schrijven:
y = 11,1432 + 1,2780*(x)
Bonus : u kunt hier een complete gids vinden voor het interpreteren van elke waarde van regressie-uitvoer in R.
Bekijk modeldiagnostische plots
We kunnen vervolgens de functie plot() gebruiken om de diagnostische plots van het regressiemodel te plotten:
#create diagnostic plots
plot(model)
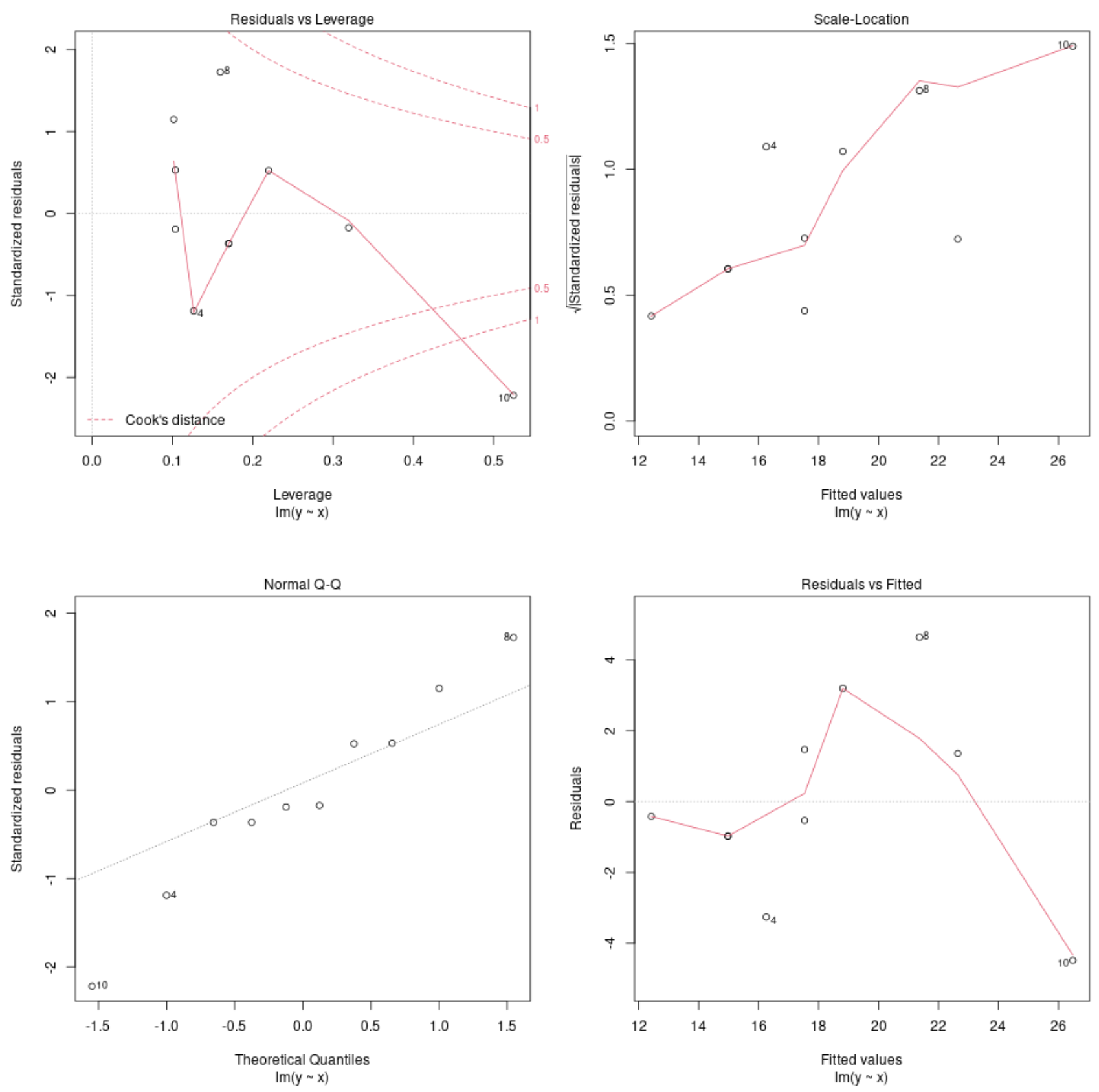
Met deze grafieken kunnen we de residuen van het regressiemodel analyseren om te bepalen of het model geschikt is om voor de gegevens te gebruiken.
Raadpleeg deze tutorial voor een volledige uitleg over het interpreteren van de diagnostische plots van een model in R.
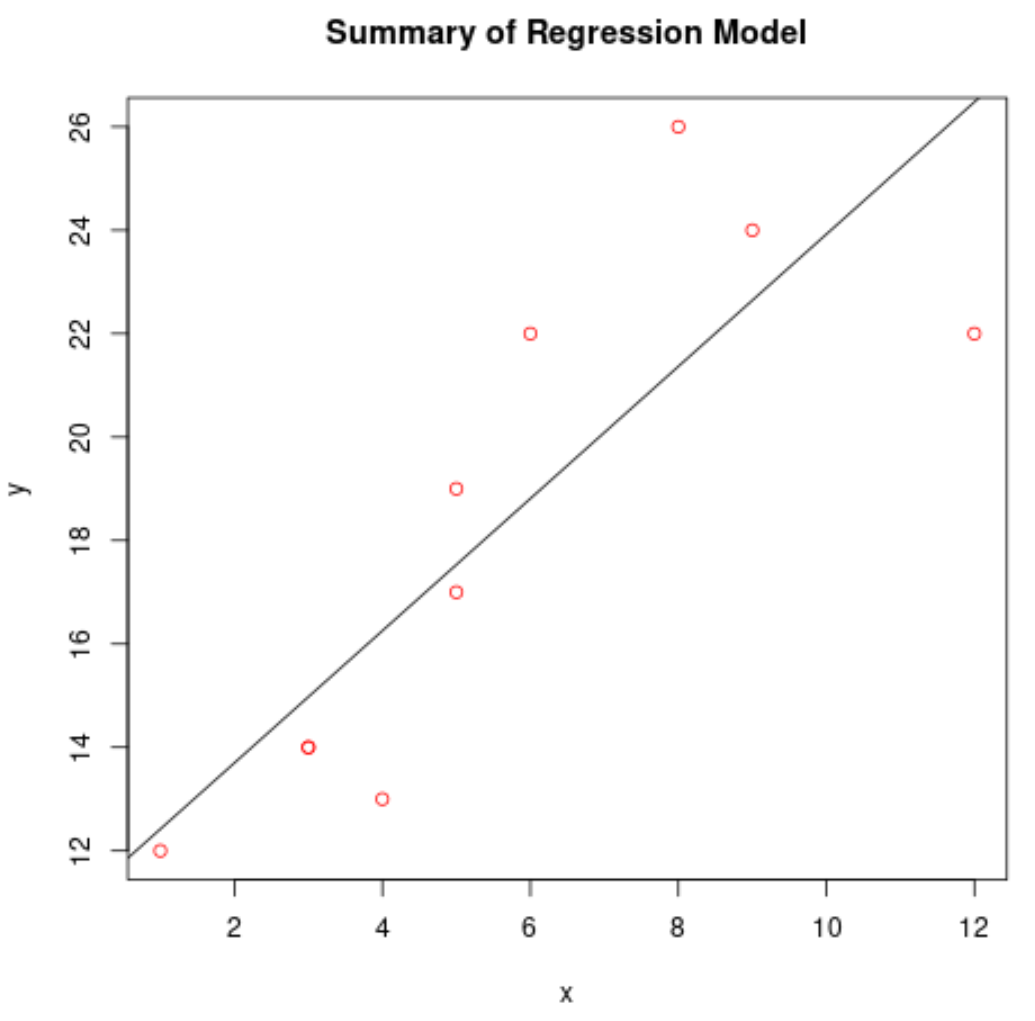
Teken het gepaste regressiemodel
We kunnen de functie abline() gebruiken om het gepaste regressiemodel te plotten:
#create scatterplot of raw data plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ') #add fitted regression line abline(model)
Gebruik het regressiemodel om voorspellingen te doen
We kunnen de functie voorspellen() gebruiken om de responswaarde voor een nieuwe waarneming te voorspellen:
#define new observation
new <- data. frame (x=c(5))
#use the fitted model to predict the value for the new observation
predict(model, newdata = new)
1
17.5332
Het model voorspelt dat deze nieuwe waarneming een responswaarde van 17,5332 zal hebben.
Aanvullende bronnen
Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe stapsgewijze regressie uit te voeren in R