Lognormale verdeling
In dit artikel wordt uitgelegd wat lognormale verdeling in statistieken is. U zult dus ontdekken wat de eigenschappen zijn van de lognormale verdeling en de grafiek van dit type kansverdeling.
Wat is de lognormale verdeling?
De lognormale verdeling , of lognormale verdeling , is een kansverdeling die een willekeurige variabele definieert waarvan de logaritme een normale verdeling volgt.
Als de variabele X dus een normale verdeling heeft, heeft de exponentiële functie ex x een lognormale verdeling.
![]()
Merk op dat de lognormale verdeling alleen kan worden gebruikt als de variabelewaarden positief zijn, aangezien de logaritme een functie is die slechts één positief argument nodig heeft.
Onder de verschillende toepassingen van de lognormale verdeling in de statistiek onderscheiden we het gebruik van deze verdeling om financiële investeringen te analyseren en betrouwbaarheidsanalyses uit te voeren.
De lognormale verdeling is ook bekend als de Tinaut-verdeling , soms ook geschreven als de lognormale verdeling of log-normale verdeling .
Plot van de lognormale verdeling
Nu we de definitie van de lognormale verdeling kennen, zullen we in deze sectie zien hoe de grafische weergave van de lognormale verdeling varieert afhankelijk van de waarden van het rekenkundig gemiddelde en de standaarddeviatie.
De grafiek van de dichtheidsfunctie van de lognormale verdeling is als volgt:
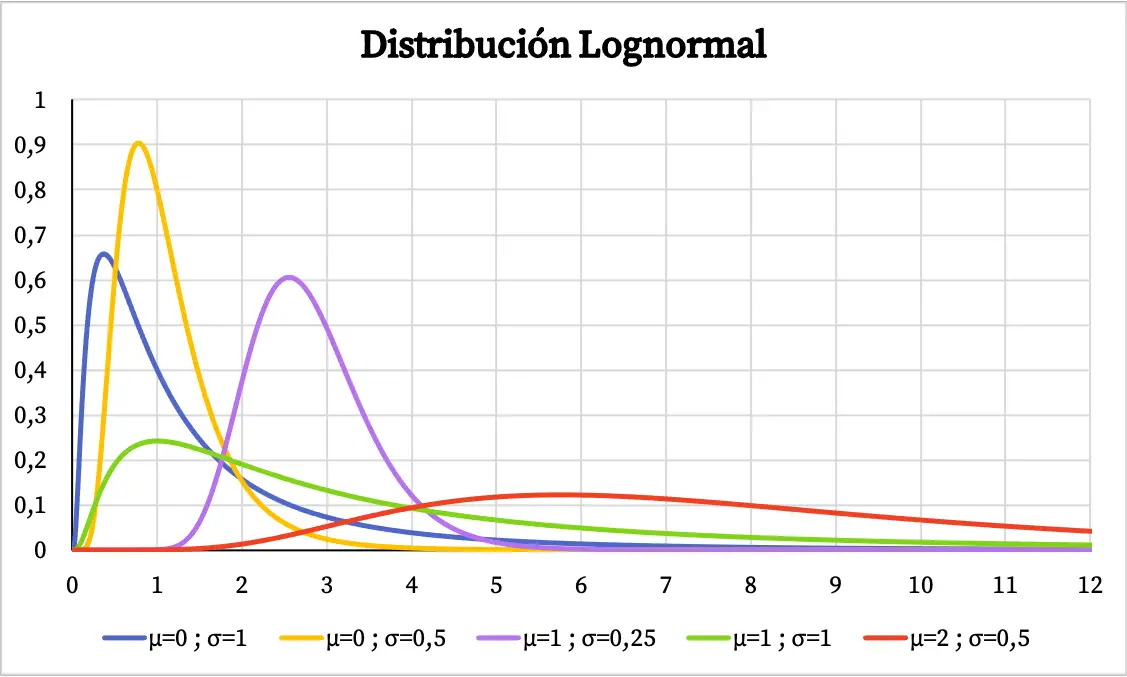
Aan de andere kant is de cumulatieve waarschijnlijkheidsgrafiek van de lognormale verdeling als volgt:
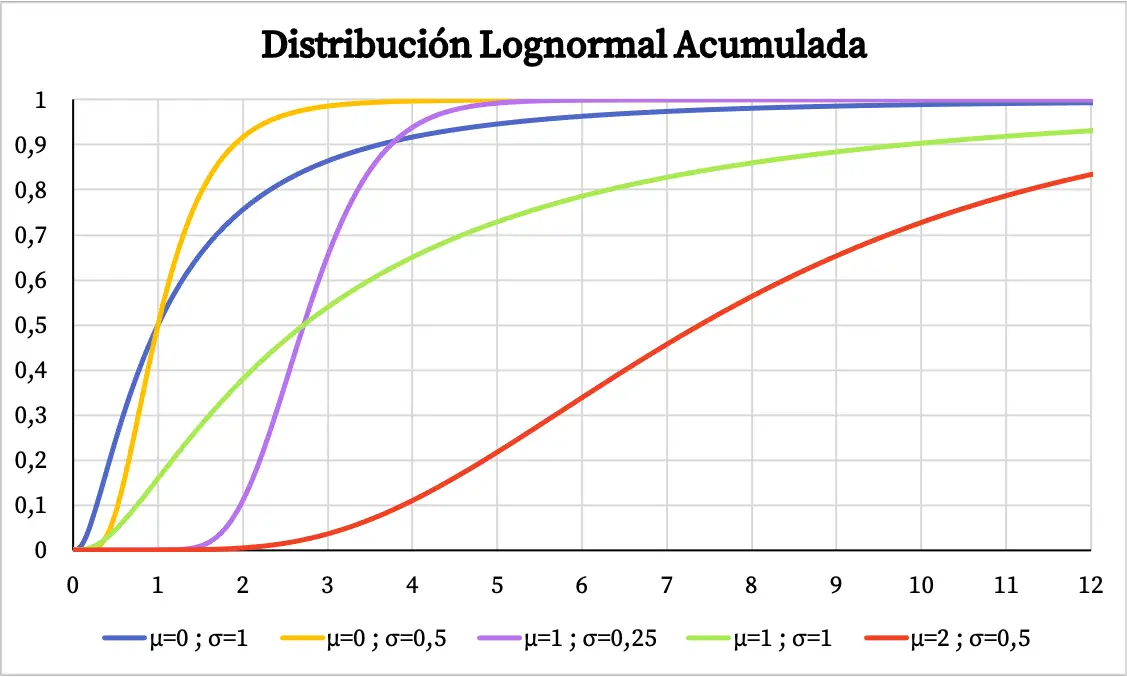
Kenmerken van de lognormale verdeling
De lognormale verdeling heeft de volgende kenmerken:
- De lognormale verdeling wordt gedefinieerd door de waarde van twee parameters, het rekenkundig gemiddelde μ en de variantie σ 2 .
![]()
- Het domein van de lognormale verdeling bestaat uit positieve reële getallen, omdat de logaritme geen negatieve of nulwaarden accepteert.
![]()
- De verwachting van een lognormale verdeling is gelijk aan het getal e verhoogd tot de som van het gemiddelde plus de variantie gedeeld door twee.
![]()
- Aan de andere kant kan de variantie van een lognormale verdeling worden berekend met de volgende uitdrukking:
![]()
- De modus van de lognormale verdeling is equivalent aan het getal e verhoogd tot het gemiddelde van de verdeling.
![]()
- De scheefheidscoëfficiënt van de lognormale verdeling kan worden bepaald door de volgende formule toe te passen:
![]()
- De formule voor de dichtheidsfunctie van de lognormale verdeling is:
![]()
- De formule voor de cumulatieve waarschijnlijkheidsfunctie van de lognormale verdeling is:
![]()
Goud
![]()
is de cumulatieve waarschijnlijkheidsfunctie van een standaard normale verdeling .
- Het rekenkundig gemiddelde van een lognormale verdeling is groter dan de waarde van de mediaan.
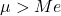
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder