Logaritmische regressie

In dit artikel wordt uitgelegd wat logaritmische regressie is en hoe deze wordt uitgevoerd. Bovendien kunt u een voorbeeld van logaritmische regressie zien om het concept volledig te begrijpen.

Wat is logaritmische regressie?

Logaritmische regressie is een regressiemodel dat een logaritme in de vergelijking bevat. Concreet wordt bij een logaritmische regressie de logaritme van de onafhankelijke variabele genomen. De vergelijking voor een logaritmisch regressiemodel is dus y=a+b·ln(x).

Logaritmische regressie is erg handig voor het aanpassen van een regressiemodel wanneer de voorbeeldgegevens een logaritmische curve vormen, zodat het regressiemodel beter bij de voorbeeldgegevens past. Hieronder zullen we zien wanneer u logaritmische regressie moet uitvoeren.

Logaritmische regressie is dus een soort niet-lineaire regressie, net als exponentiële regressie en polynomiale regressie.

Logaritmische regressieformule

Een logaritmisch regressiemodel omvat het nemen van de logaritme van de onafhankelijke variabele. Daarom is de formule voor de vergelijking van een logaritmische regressie y=a+b·ln(x).

Goud:

• 

  is de afhankelijke variabele.

• 

  is de onafhankelijke variabele.

• 

  zijn de regressiecoëfficiënten.

Merk op dat y=a+b·ln(x) feitelijk de vergelijking van een lijn is, maar in plaats van te verwijzen naar de oorspronkelijke variabelen x en y, verwijst deze naar de variabelen ln(x) en y.

Wanneer logaritmische regressie uitvoeren?

We moeten logaritmische regressie uitvoeren als de grafiek van de voorbeeldgegevens een logaritmische curve is, dat wil zeggen als de grafiek van de punten vergelijkbaar is met de grafiek van een logaritmische functie.

Kijk naar het onderstaande spreidingsdiagram. Er werd een lineair regressiemodel aan een dataset aangepast. Zoals je kunt zien is de lijn geen slechte benadering van de gegevens, maar als je voorzichtig bent, stijgen de waarden aan het begin van de grafiek sneller dan aan het einde, waardoor de lijn niet helemaal overeenkomt met de waarnemingen .

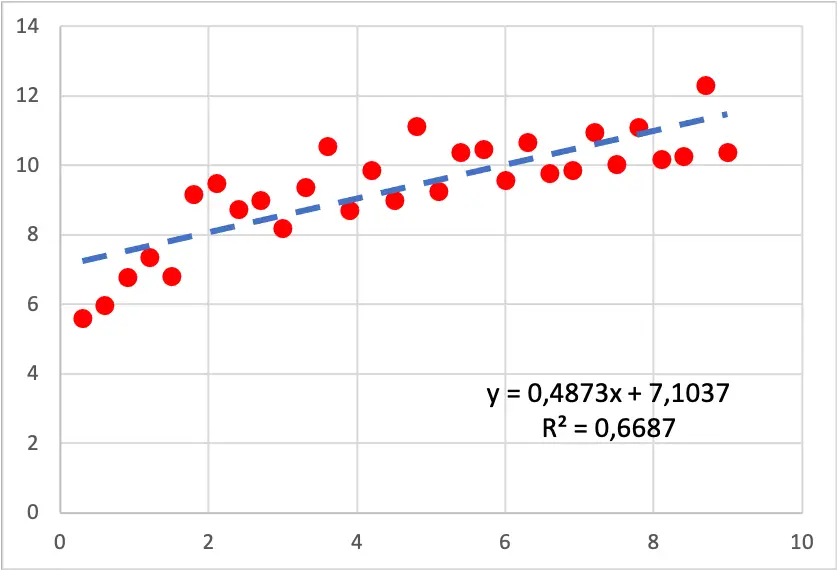
Het is dus de moeite waard om een logaritmisch regressiemodel te maken, omdat het lijkt alsof de gegevens een logaritmische curve volgen. Het resultaat verkregen uit het logaritmische regressiemodel is als volgt:

Zoals u in de vorige grafiek kunt zien, past het resulterende logaritmische regressiemodel beter bij de voorbeeldgegevens. In feite is de determinatiecoëfficiënt gestegen van 66,87% naar 80,05%, zodat het model de gegevenssteekproef nu beter kan verklaren. Daarom is het in dit geval beter om logistische regressie te gebruiken om een vergelijking te vinden die de gegevenswaarde benadert.

Andere soorten niet-lineaire regressie

De drie meest voorkomende gevallen van niet-lineaire regressie zijn:

• Logaritmische regressie : de logaritme van de onafhankelijke variabele wordt genomen.
• Exponentiële regressie : de onafhankelijke variabele is de exponent van de vergelijking.
• Polynoomregressie : de regressiemodelvergelijking heeft de vorm van een polynoom.