Logistieke regressie

Von Dr.benjamin anderson August 2, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat logistieke regressie in de statistiek is. Op dezelfde manier vindt u de logistische regressieformule, wat de verschillende soorten logistische regressie zijn en bovendien een opgeloste logistische regressieoefening.

Wat is logistische regressie?

In de statistieken is logistische regressie een type regressiemodel dat wordt gebruikt om de uitkomst van een categorische variabele te voorspellen. Dat wil zeggen dat logistieke regressie wordt gebruikt om de waarschijnlijkheid te modelleren dat een categorische variabele een bepaalde waarde aanneemt op basis van de onafhankelijke variabelen.

Het meest gebruikelijke logistieke regressiemodel is binaire logistische regressie, waarbij er slechts twee mogelijke uitkomsten zijn: „mislukking“ of „succes“ ( Bernoulli-verdeling ). “Mislukking” wordt weergegeven door de waarde 0, terwijl “succes” wordt weergegeven door de waarde 1.

De kans dat een student slaagt voor een examen op basis van de uren die hij of zij aan studeren heeft besteed, kan bijvoorbeeld worden bestudeerd met behulp van een logistisch regressiemodel. In dit geval zou falen het resultaat zijn van ‘mislukking’ en aan de andere kant zou succes het gevolg zijn van ‘succes’.

Logistieke regressieformule

De vergelijking voor een logistisch regressiemodel is:

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

Daarom wordt in een logistisch regressiemodel de waarschijnlijkheid van het verkrijgen van het ‘succes’-resultaat, dat wil zeggen dat de afhankelijke variabele de waarde 1 aanneemt, berekend met de volgende formule:

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

Goud:

$p$

is de kans dat de afhankelijke variabele 1 is.
$\beta_0$

is de constante van het logistische regressiemodel.
$\beta_i$

is de regressiecoëfficiënt van variabele i.
$x_i$

is de waarde van variabele i.

Voorbeeld van een logistiek regressiemodel

Nu we de definitie van logistische regressie kennen, gaan we een concreet voorbeeld bekijken van hoe we een model van dit type regressie kunnen maken.

In de volgende tabel is een reeks van twintig gegevens verzameld die betrekking hebben op de studie-uren van elke student en op het feit of hij wel of niet geslaagd is voor een statistiekexamen. Voer een logistisch regressiemodel uit en bereken de kans dat een student slaagt als hij of zij 4 uur heeft gestudeerd.

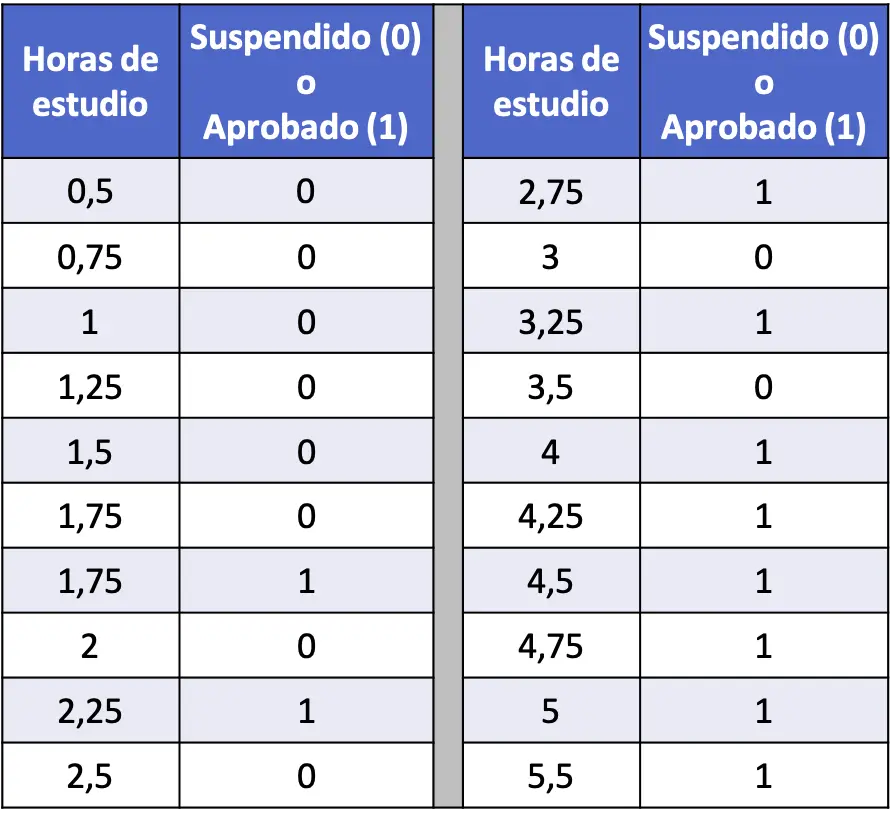
In dit geval is de verklarende variabele het aantal studie-uren en de responsvariabele of de student niet geslaagd (0) of geslaagd (1) is. Daarom hebben we in ons model alleen de coëfficiënt

$\beta_0$

en de coëfficiënt

$\beta_1$

, omdat er maar één onafhankelijke variabele is.

$\beta_0 \qquad \beta_1$

Handmatige bepaling van regressiecoëfficiënten is zeer bewerkelijk, daarom wordt aanbevolen computersoftware zoals Minitab te gebruiken. De waarden van de regressiecoëfficiënten berekend met Minitab zijn dus als volgt:

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

Het logistische regressiemodel is daarom als volgt:

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

Hieronder ziet u de voorbeeldgegevens en de logistische regressiemodelvergelijking grafisch weergegeven:

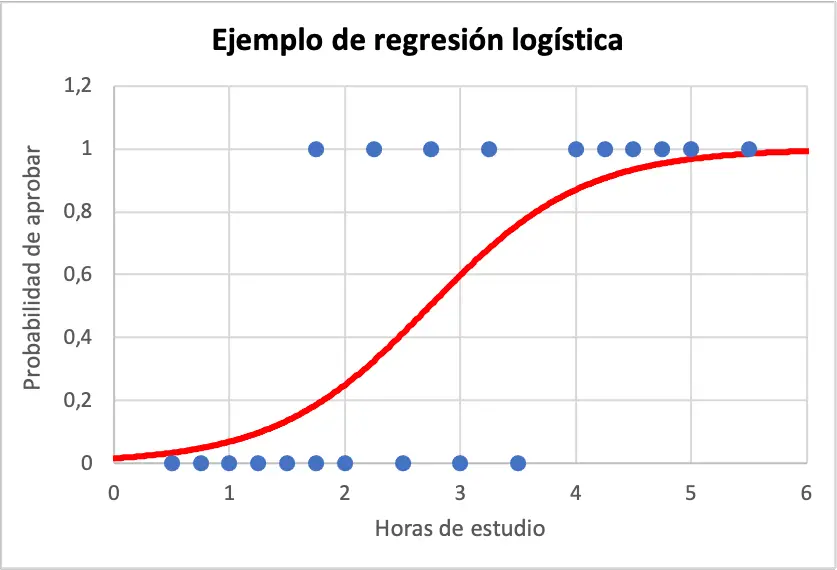
Om dus de waarschijnlijkheid te berekenen dat een student zal slagen als hij of zij 4 uur heeft gestudeerd, gebruikt u eenvoudigweg de vergelijking die is verkregen uit het logistische regressiemodel:

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

Kortom, als een student vier uur studeert, heeft hij een kans van 86,99% om het examen te halen.

Soorten logistieke regressie

Er zijn drie soorten logistische regressie :

Binaire logistieke regressie : de afhankelijke variabele kan slechts twee waarden hebben (0 en 1).
Multinomiale logistische regressie : de afhankelijke variabele heeft meer dan twee mogelijke waarden.
Ordinale logistische regressie : mogelijke uitkomsten hebben een natuurlijke volgorde.

Logistieke regressie en lineaire regressie

Ten slotte zullen we samenvattend zien wat het verschil is tussen een logistische regressie en een lineaire regressie, aangezien het meest gebruikte regressiemodel in de statistiek het lineaire model is.

Lineaire regressie wordt gebruikt om numeriek afhankelijke variabelen te modelleren. Bovendien is bij lineaire regressie de relatie tussen de verklarende variabelen en de responsvariabele lineair.

Daarom is het belangrijkste verschil tussen logistische regressie en lineaire regressie het type afhankelijke variabele. Bij een logistieke regressie is de afhankelijke variabele categorisch, terwijl de afhankelijke variabele bij een lineaire regressie numeriek is.

Logistische regressie wordt dus gebruikt om een uitkomst tussen twee mogelijke opties te voorspellen, terwijl lineaire regressie helpt een numerieke uitkomst te voorspellen.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder