Hoe logistische regressie uit te voeren in sas

Logistische regressie is een methode die we kunnen gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is.

Logistische regressie maakt gebruik van een methode die bekend staat als maximale waarschijnlijkheidsschatting om een vergelijking van de volgende vorm te vinden:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Goud:

• _Xj : de j ^-de voorspellende variabele
• β _j : schatting van de coëfficiënt voor de j ^-de voorspellende variabele

De formule aan de rechterkant van de vergelijking voorspelt de logkans dat de responsvariabele de waarde 1 aanneemt.

In het volgende stapsgewijze voorbeeld ziet u hoe u een logistisch regressiemodel in SAS kunt passen.

Stap 1: Maak de gegevensset

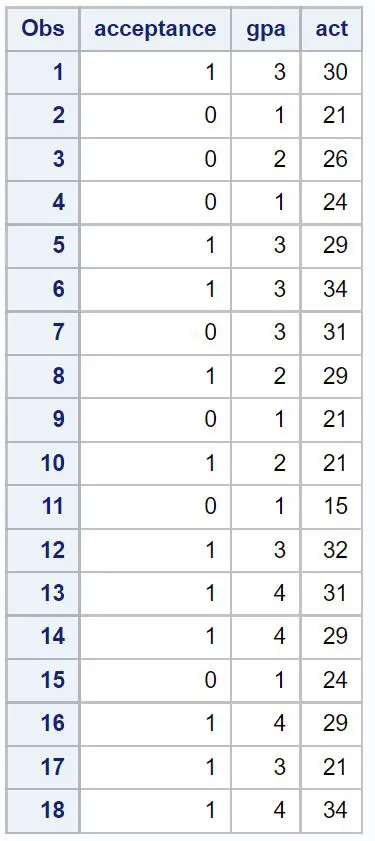
Eerst zullen we voor 18 studenten een dataset maken met informatie over de volgende drie variabelen:

• Toelating tot een bepaalde universiteit (1 = ja, 0 = nee)
• GPA (schaal van 1 tot 4)
• ACT-score (schaal van 1 tot 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

Stap 2: Pas het logistische regressiemodel aan

Vervolgens zullen we proc-logistiek gebruiken om in het logistische regressiemodel te passen, waarbij we „acceptatie“ gebruiken als de responsvariabele en „gpa“ en „act“ als de voorspellende variabelen.

Opmerking : SAS moet afnemend worden opgegeven om de waarschijnlijkheid te voorspellen dat de responsvariabele de waarde 1 zal aannemen. SAS voorspelt standaard de waarschijnlijkheid dat de responsvariabele de waarde 0 zal aannemen.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

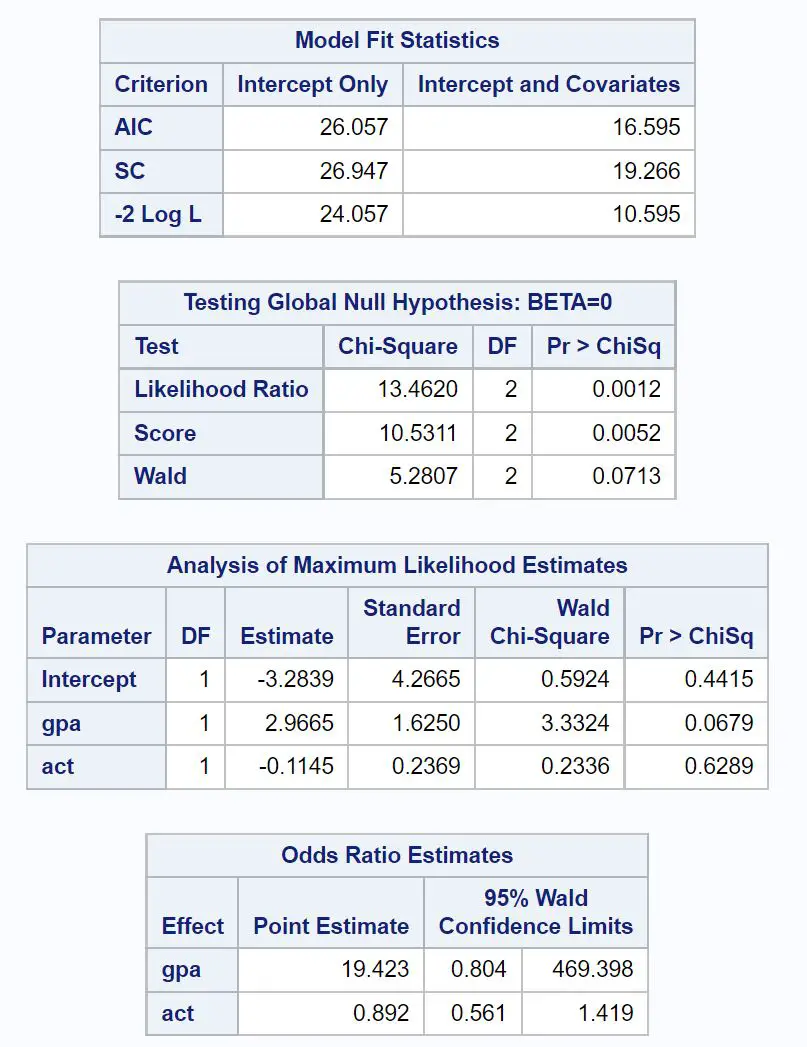
De eerste interessante tabel is getiteld Model Fit Statistics .

Uit deze tabel kunnen we de AIC-waarde van het model zien, die 16.595 blijkt te zijn. Hoe lager de AIC-waarde, hoe beter het model in de gegevens kan passen.

Er is echter geen drempel voor wat als een „goede“ AIC-waarde wordt beschouwd. In plaats daarvan gebruiken we AIC om de fit van meerdere modellen met dezelfde dataset te vergelijken. Het model met de laagste AIC-waarde wordt over het algemeen als het beste beschouwd.

De volgende interessante tabel is getiteld Testing the Global Null Hypothesis: BETA=0 .

Uit deze tabel kunnen we de chi-kwadraatwaarde van de waarschijnlijkheidsratio van 13,4620 zien met een overeenkomstige p-waarde van 0,0012 .

Omdat deze p-waarde kleiner is dan 0,05, vertelt dit ons dat het logistische regressiemodel als geheel statistisch significant is.

Vervolgens kunnen we de coëfficiëntschattingen analyseren in de tabel met de titel Analyse van maximale waarschijnlijkheidsschattingen .

Uit deze tabel kunnen we de coëfficiënten voor gpa en act zien, die de gemiddelde verandering aangeven in de logkans om toegelaten te worden tot de universiteit bij een stijging van één eenheid in elke variabele.

Bijvoorbeeld:

• Een stijging van één eenheid in de GPA-waarde gaat gepaard met een gemiddelde stijging van 2,9665 in de logkans om te worden toegelaten tot de universiteit.
• Een stijging met één eenheid in de ACT-score gaat gepaard met een gemiddelde daling van 0,1145 in de logkans om toegelaten te worden tot de universiteit.

De overeenkomstige p-waarden in het resultaat geven ons ook een idee van hoe effectief elke voorspellende variabele is bij het voorspellen van de waarschijnlijkheid van acceptatie:

• GPA P-waarde: 0,0679
• ACT P-waarde: 0,6289

Dit vertelt ons dat GPA een statistisch significante voorspeller lijkt te zijn van acceptatie door een universiteit, terwijl de ACT-score niet statistisch significant lijkt te zijn.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere regressiemodellen in SAS kunt passen:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS