Logistische regressie versus lineaire regressie: de belangrijkste verschillen
Twee van de meest gebruikte regressiemodellen zijn lineaire regressie en logistische regressie .
Beide soorten regressiemodellen worden gebruikt om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te kwantificeren, maar er zijn een paar belangrijke verschillen tussen de twee modellen:
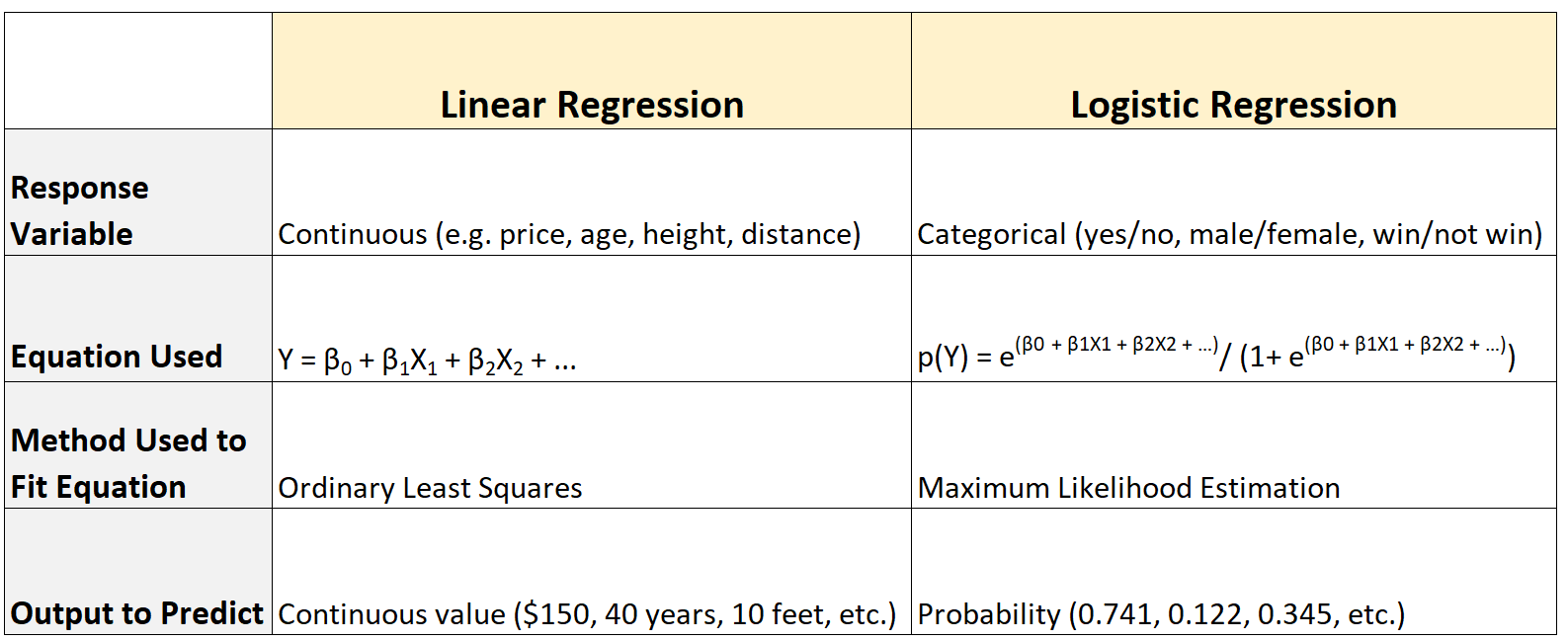
Hier is een samenvatting van de verschillen:
Verschil #1: Type responsvariabele
Een lineair regressiemodel wordt gebruikt wanneer de responsvariabele een continue waarde aanneemt, zodat:
- Prijs
- Hoogte
- Leeftijd
- Afstand
Omgekeerd wordt een logistisch regressiemodel gebruikt wanneer de responsvariabele een categorische waarde aanneemt, zoals:
- Ja of nee
- Man of vrouw
- Winnen of niet winnen
Verschil #2: gebruikte vergelijking
Bij lineaire regressie wordt de volgende vergelijking gebruikt om de relatie tussen de voorspellende variabele(n) en de responsvariabele samen te vatten:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Goud:
- Y: de responsvariabele
- Xj : de j -de voorspellende variabele
- βj : Het gemiddelde effect op Y van een toename van één eenheid in Xj , waarbij alle andere voorspellers vast blijven
Omgekeerd gebruikt logistische regressie de volgende vergelijking:
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p
Deze vergelijking wordt gebruikt om de waarschijnlijkheid te voorspellen dat een individuele waarneming in een bepaalde categorie valt.
Verschil #3: Methode die wordt gebruikt om aan de vergelijking te voldoen
Lineaire regressie maakt gebruik van een methode die bekend staat als gewone kleinste kwadraten om de best passende regressievergelijking te vinden.
Omgekeerd gebruikt logistische regressie een methode die bekend staat als maximale waarschijnlijkheidsschatting om de best passende regressievergelijking te vinden.
Verschil #4: te voorspellen output
Lineaire regressie voorspelt een continue waarde als output. Bijvoorbeeld:
- Prijs ($ 150, $ 199, $ 400, enz.)
- Hoogte (14 inch, 2 voet, 94,32 centimeter, enz.)
- Leeftijd (2 maanden, 6 jaar, 41,5 jaar, enz.)
- Afstand (1,23 mijl, 4,5 kilometer, enz.)
Omgekeerd voorspelt logistische regressie waarschijnlijkheden als uitkomst. Bijvoorbeeld:
- 40,3% kans om toegelaten te worden tot een universiteit.
- 93,2% kans om een spel te winnen.
- 34,2% kans dat een wet wordt aangenomen.
Wanneer logistische of lineaire regressie gebruiken?
De volgende oefenproblemen kunnen u helpen beter te begrijpen wanneer u logistische regressie of lineaire regressie moet gebruiken.
Probleem #1: Jaarinkomen
Stel dat een econoom voorspellende variabelen (1) wekelijkse gewerkte uren en (2) jaren opleiding wil gebruiken om het jaarinkomen van individuen te voorspellen.
In dit scenario zou hij lineaire regressie gebruiken omdat de responsvariabele (jaarinkomen) continu is.
Probleem #2: acceptatie door de universiteit
Stel dat een toelatingsfunctionaris van een universiteit de voorspellende variabelen (1) GPA en (2) ACT-score wil gebruiken om de waarschijnlijkheid te voorspellen dat een student wordt toegelaten tot een bepaalde universiteit.
In dit scenario zou ze logistieke regressie gebruiken omdat de responsvariabele categorisch is en slechts twee waarden kan aannemen: geaccepteerd of niet geaccepteerd.
Probleem #3: Vastgoedprijzen
Stel dat een makelaar de voorspellende variabelen (1) vierkante meters, (2) aantal slaapkamers en (3) aantal badkamers wil gebruiken om de verkoopprijzen van huizen te voorspellen.
In dit scenario zou ze lineaire regressie gebruiken omdat de responsvariabele (prijs) continu is.
Probleem #4: Spamdetectie
Stel dat een computerprogrammeur de voorspellende variabelen (1) het aantal woorden en (2) het land van herkomst wil gebruiken om de waarschijnlijkheid te voorspellen dat een bepaalde e-mail spam is.
In dit scenario zou logistische regressie worden gebruikt omdat de responsvariabele categorisch is en slechts twee waarden kan aannemen: spam of geen spam.
Aanvullende bronnen
De volgende tutorials bieden meer details over lineaire regressie:
- Inleiding tot eenvoudige lineaire regressie
- Inleiding tot meervoudige lineaire regressie
- 4 voorbeelden van het gebruik van lineaire regressie in het echte leven
De volgende tutorials bieden meer details over logistische regressie:
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder