Logistieke regressie uitvoeren in python (stap voor stap)

Logistische regressie is een methode die we kunnen gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is.

Logistische regressie maakt gebruik van een methode die bekend staat als maximale waarschijnlijkheidsschatting om een vergelijking van de volgende vorm te vinden:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Goud:

• _Xj : de j ^-de voorspellende variabele
• β _j : schatting van de coëfficiënt voor de j ^-de voorspellende variabele

De formule aan de rechterkant van de vergelijking voorspelt de logkans dat de responsvariabele de waarde 1 aanneemt.

Dus als we een logistisch regressiemodel passen, kunnen we de volgende vergelijking gebruiken om de waarschijnlijkheid te berekenen dat een bepaalde waarneming de waarde 1 aanneemt:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Vervolgens gebruiken we een bepaalde waarschijnlijkheidsdrempel om de waarneming als 1 of 0 te classificeren.

We zouden bijvoorbeeld kunnen zeggen dat waarnemingen met een waarschijnlijkheid groter dan of gelijk aan 0,5 als „1“ worden geclassificeerd en dat alle andere waarnemingen als „0“ worden geclassificeerd.

Deze zelfstudie biedt een stapsgewijs voorbeeld van het uitvoeren van logistische regressie in R.

Stap 1: Importeer de benodigde pakketten

Eerst zullen we de benodigde pakketten importeren om logistieke regressie in Python uit te voeren:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Stap 2: Gegevens laden

Voor dit voorbeeld gebruiken we de standaarddataset uit het boek Introduction to Statistical Learning . We kunnen de volgende code gebruiken om een samenvatting van de dataset te laden en weer te geven:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

Deze dataset bevat de volgende informatie over 10.000 personen:

• standaard: geeft aan of een persoon in gebreke is gebleven of niet.
• student: geeft aan of een persoon student is of niet.
• saldo: Gemiddeld saldo dat door een individu wordt bijgehouden.
• inkomen: inkomen van het individu.

We zullen de studentenstatus, banksaldo en inkomen gebruiken om een logistisch regressiemodel te construeren dat de waarschijnlijkheid voorspelt dat een bepaald individu in gebreke blijft.

Stap 3: Maak trainings- en testvoorbeelden

Vervolgens splitsen we de dataset op in een trainingsset om het model op te trainen en een testset om het model op te testen .

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

Stap 4: Pas het logistische regressiemodel aan

Vervolgens zullen we de functie LogisticRegression() gebruiken om een logistisch regressiemodel aan de dataset te koppelen:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

Stap 5: Modeldiagnostiek

Zodra we het regressiemodel hebben aangepast, kunnen we de prestaties van ons model op de testdataset analyseren.

Eerst zullen we de verwarringsmatrix voor het model maken:

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

Uit de verwarringsmatrix kunnen we zien dat:

• #Echte positieve voorspellingen: 2886
• #Echte negatieve voorspellingen: 0
• #Vals-positieve voorspellingen: 113
• #Vals-negatieve voorspellingen: 1

We kunnen ook het nauwkeurigheidsmodel verkrijgen, dat ons het percentage correctievoorspellingen vertelt dat door het model wordt gedaan:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

Dit vertelt ons dat het model in 96,2% van de gevallen de juiste voorspelling deed over de vraag of een individu wel of niet in gebreke zou blijven.

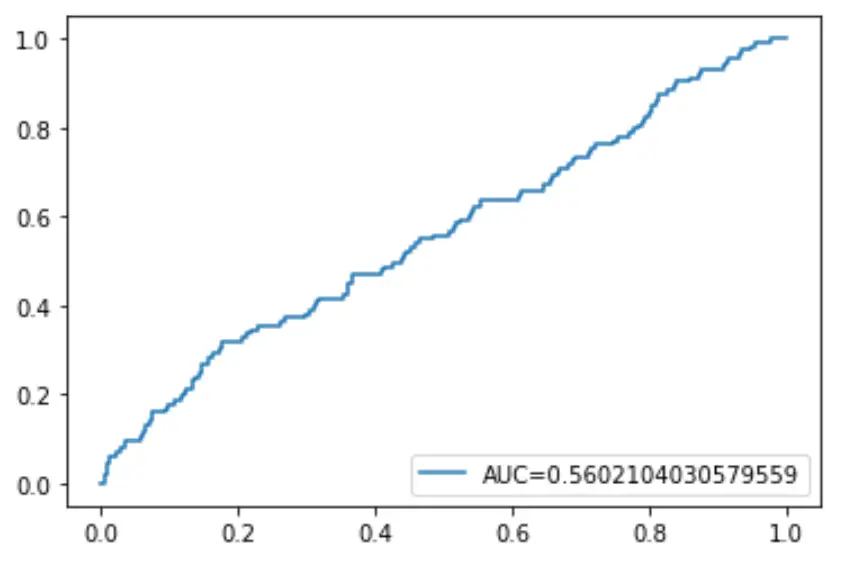
Ten slotte kunnen we de Receiver Operating Characteristic (ROC)-curve uitzetten, die het percentage echte positieven weergeeft dat door het model wordt voorspeld wanneer de voorspellingswaarschijnlijkheidsdrempel wordt verlaagd van 1 naar 0.

Hoe hoger de AUC (gebied onder de curve), hoe nauwkeuriger ons model de resultaten kan voorspellen:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()