Hoe loess-regressie in r uit te voeren (met voorbeeld)

LOESS-regressie , ook wel lokale regressie genoemd, is een methode die lokale aanpassing gebruikt om een regressiemodel aan te passen aan een reeks gegevens.

Het volgende stapsgewijze voorbeeld laat zien hoe u LOESS-regressie uitvoert in R.

Stap 1: Creëer de gegevens

Laten we eerst het volgende dataframe in R maken:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Stap 2: Pas meerdere LOESS-regressiemodellen toe

We kunnen de löss() -functie gebruiken om meerdere LOESS-regressiemodellen in deze dataset te passen, met verschillende waarden voor de span- parameter:

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

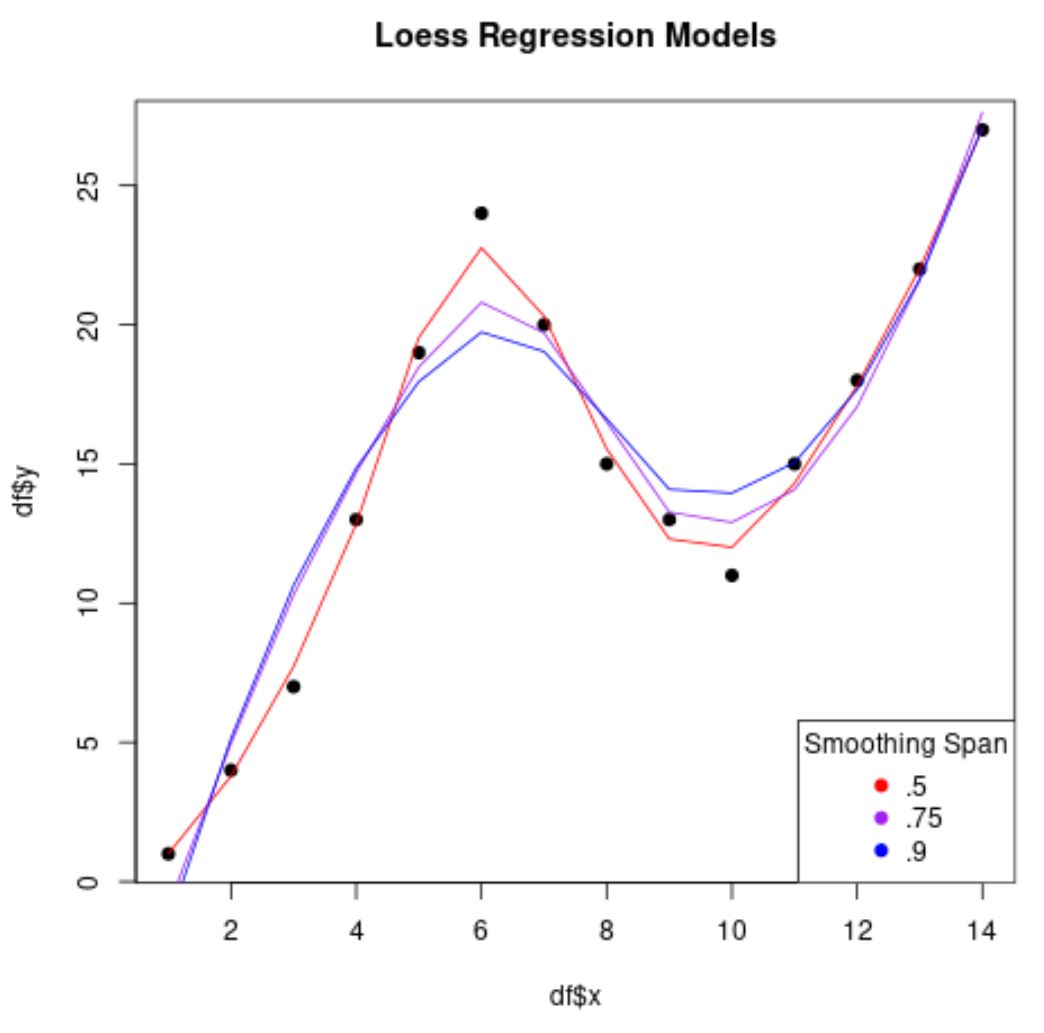
Merk op dat hoe lager de waarde die we gebruiken voor span , hoe minder “glad” het regressiemodel zal zijn en hoe meer het model zal proberen de gegevenspunten te passen.

Stap 3: Gebruik K-Fold Cross-Validation om het beste model te vinden

Om de optimale omvangswaarde te vinden die we kunnen gebruiken, kunnen we k-voudige kruisvalidatie uitvoeren met behulp van functies in het caret- pakket:

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

We kunnen zien dat de spanwaarde die de laagste waarde voor de root mean square error (RMSE) opleverde, 0,7 is.

Voor ons uiteindelijke LOESS-regressiemodel zouden we er dus voor kiezen om een waarde van 0,7 te gebruiken voor het span- argument in de löss()- functie.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over regressiemodellen in R:

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe logistische regressie uit te voeren in R
Hoe kwantielregressie uit te voeren in R
Hoe gewogen regressie uit te voeren in R