Mae versus rmse: welke maatstaf moet u gebruiken?

Regressiemodellen worden gebruikt om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te kwantificeren.

Wanneer we een regressiemodel passen, willen we begrijpen hoe goed het model in staat is de waarden van de voorspellende variabelen te gebruiken om de waarde van de responsvariabele te voorspellen.

Twee maatstaven die we vaak gebruiken om te kwantificeren hoe goed een model bij een dataset past, zijn de gemiddelde absolute fout (MAE) en de root mean square error (RMSE), die als volgt worden berekend:

MAE : Een metriek die ons het gemiddelde absolute verschil vertelt tussen voorspelde waarden en werkelijke waarden in een dataset. Hoe lager de MAE, hoe beter een model bij een dataset past.

MAE = 1/n * Σ|y _i – ŷ _i |

Goud:

• Σ is een symbool dat “som” betekent
• y _i is de waargenomen waarde voor de ^i-de waarneming
• ŷ _i is de voorspelde waarde voor de i- ^de waarneming
• n is de steekproefomvang

RMSE : Een metriek die ons de vierkantswortel vertelt van het wortelgemiddelde kwadratische verschil tussen de voorspelde waarden en de werkelijke waarden in een dataset. Hoe lager de RMSE, hoe beter een model bij een dataset past.

Het wordt als volgt berekend:

RMSE = √ Σ(y _ik – ŷ _ik ) ² / n

Goud:

• Σ is een symbool dat “som” betekent
• ŷ _i is de voorspelde waarde voor de i- ^de waarneming
• y _i is de waargenomen waarde voor de ^i-de waarneming
• n is de steekproefomvang

Voorbeeld: Berekening van RMSE en MAE

Stel dat we een regressiemodel gebruiken om te voorspellen hoeveel punten 10 spelers zullen scoren in een basketbalwedstrijd.

De volgende tabel toont de door het model voorspelde punten, vergeleken met de daadwerkelijke punten die door de spelers zijn gescoord:

Met behulp van de MAE-calculator kunnen we berekenen dat de MAE 3,2 is.

Dit vertelt ons dat het gemiddelde absolute verschil tussen de door het model voorspelde waarden en de werkelijke waarden 3,2 bedraagt.

Met behulp van de RMSE-calculator kunnen we berekenen dat de RMSE gelijk is aan 4 .

Dit vertelt ons dat de vierkantswortel van de wortel van het gemiddelde kwadratische verschil tussen de voorspelde gescoorde punten en de daadwerkelijk gescoorde punten 4 is.

Houd er rekening mee dat elke metriek ons een idee geeft van het typische verschil tussen de voorspelde waarde van het model en de werkelijke waarde in de dataset, maar de interpretatie van elke metriek is enigszins anders.

RMSE versus MAE: welke maatstaf moet u gebruiken?

Als je meer gewicht wilt toekennen aan waarnemingen die verder van het gemiddelde liggen (dat wil zeggen als een afwijking van 20 meer dan twee keer zo erg is als een afwijking van 10), is het beter om de RMSE te gebruiken om fouten te meten, omdat de RMSE gevoeliger voor waarnemingen verder van het gemiddelde.

Als ‚offset‘ zijn op 20 echter twee keer zo erg is als ‚offset‘ zijn op 10, dan is het beter om de MAE te gebruiken.

Om dit te illustreren, stel dat we een speler hebben die een duidelijke uitschieter is in termen van het aantal gescoorde punten:

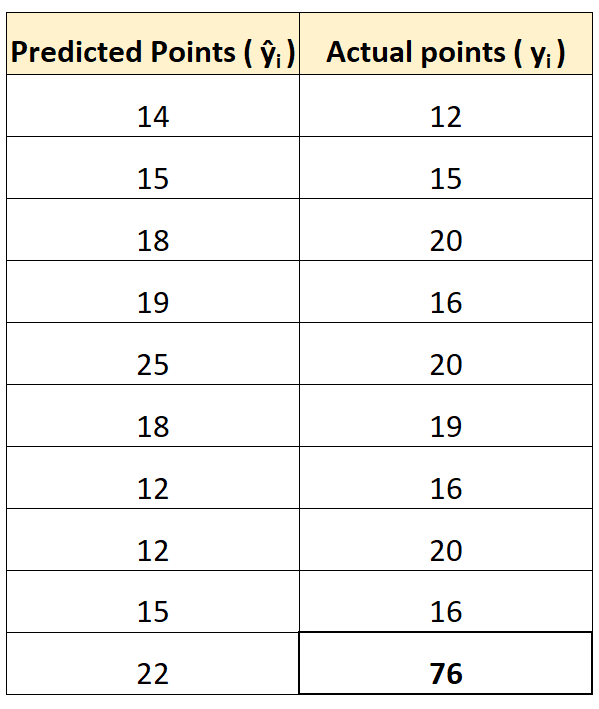
Met behulp van de eerder genoemde online rekenmachines kunnen we de MAE en RMSE als volgt berekenen:

• MAE : 8
• RMSE : 16.4356

Merk op dat de RMSE veel meer stijgt dan de MAE.

Dit komt omdat RMSE kwadratische verschillen in zijn formule gebruikt en het kwadratische verschil tussen de waargenomen waarde van 76 en de voorspelde waarde van 22 vrij groot is. Dit resulteert in een aanzienlijke stijging van de RMSE-waarde.

In de praktijk passen we doorgaans meerdere regressiemodellen in een dataset en berekenen we voor elk model slechts één van deze statistieken.

We zouden bijvoorbeeld drie verschillende regressiemodellen kunnen passen en de RMSE voor elk model kunnen berekenen. We zouden dan het model met de laagste RMSE-waarde als het ‘beste’ model selecteren, omdat dit het model is dat de voorspellingen doet die het dichtst bij de werkelijke waarden in de dataset liggen.

Zorg er in beide gevallen voor dat u voor elk model dezelfde statistiek berekent. Bereken bijvoorbeeld niet de MAE voor het ene model en de RMSE voor een ander model en vergelijk vervolgens deze twee metingen.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u MAE kunt berekenen met behulp van verschillende statistische software:

Hoe de gemiddelde absolute fout in Excel te berekenen
Hoe de gemiddelde absolute fout in R te berekenen
Hoe de gemiddelde absolute fout in Python te berekenen

In de volgende tutorials wordt uitgelegd hoe u RMSE kunt berekenen met behulp van verschillende statistische software:

Hoe de gemiddelde vierkante fout in Excel te berekenen
Hoe de gemiddelde kwadratische fout in R te berekenen
Hoe de gemiddelde kwadratische fout in Python te berekenen