Mann-whitney u-test
Een Mann-Whitney U-test (ook wel een Wilcoxon-rangsomtest genoemd) wordt gebruikt om verschillen tussen twee onafhankelijke steekproeven te vergelijken wanneer de steekproefverdelingen niet normaal verdeeld zijn en de steekproefomvang klein is (n <30).
Het wordt beschouwd als het niet-parametrische equivalent van de onafhankelijke t-test met twee steekproeven .
Hier zijn enkele voorbeelden van wanneer u een Mann-Whitney U-test kunt gebruiken:
- U wilt de salarissen van vijf afgestudeerden van universiteit A vergelijken met de salarissen van vijf afgestudeerden van universiteit B. Salarissen zijn niet normaal verdeeld.
- Je wilt weten of het gewichtsverlies varieert voor twee groepen: 12 mensen die dieet A gebruiken en 10 mensen die dieet B gebruiken. Het gewichtsverlies is niet normaal verdeeld.
- Je wilt weten of de scores van 8 leerlingen uit klas A verschillen van die van 7 leerlingen uit klas B. De scores zijn niet normaal verdeeld.
In elk voorbeeld wil je twee groepen vergelijken, de steekproefverdelingen zijn niet normaal en de steekproefomvang is klein.
Een Mann-Whitney U-test is dus geschikt zolang aan de volgende aannames wordt voldaan.
Mann-Whitney U-testaannames
Voordat u een Mann-Whitney U-test uitvoert, moet u ervoor zorgen dat aan de volgende vier aannames wordt voldaan:
- Gewoon of continu: De variabele die u analyseert is ordinaal of continu. Voorbeelden van ordinale variabelen zijn Likert-items (bijvoorbeeld een vijfpuntsschaal variërend van “helemaal mee oneens” tot “helemaal mee eens”). Voorbeelden van continue variabelen zijn lengte (gemeten in inches), gewicht (gemeten in ponden) of testscores (gemeten van 0 tot 100).
- Onafhankelijkheid: Alle waarnemingen van beide groepen zijn onafhankelijk van elkaar.
- Vorm: De vormen van de verdelingen voor de twee groepen zijn ongeveer hetzelfde.
Als aan deze aannames wordt voldaan, kunt u een Mann-Whitney U-test uitvoeren.
Hoe u een Mann-Whitney U-test uitvoert
Om een Mann-Whitney U-test uit te voeren, volgen we de standaard procedure voor het testen van hypothesen in vijf stappen :
1. Geef de aannames weer.
In de meeste gevallen wordt de Mann-Whitney U-test uitgevoerd als een tweezijdige test. De nul- en alternatieve hypothesen zijn geschreven in de vorm:
H 0 : De twee populaties zijn gelijk
H a : De twee populaties zijn niet gelijk
2. Bepaal een significantieniveau dat voor de hypothese moet worden gebruikt.
Bepaal een significantieniveau. Veel voorkomende keuzes zijn .01, .05 en .1.
3. Zoek de teststatistiek.
De teststatistiek wordt aangegeven met U en is de kleinste van U 1 en U 2 , zoals hieronder gedefinieerd:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
waarbij n 1 en n 2 de steekproefgroottes zijn voor respectievelijk monsters 1 en 2, en R 1 en R 2 de som zijn van de rangen voor respectievelijk monsters 1 en 2.
De onderstaande voorbeelden laten zien hoe u deze teststatistiek in detail kunt vinden.
4. Verwerp de nulhypothese of verwerp deze niet.
Bepaal met behulp van de teststatistieken of u de nulhypothese wel of niet kunt verwerpen op basis van het significantieniveau en de kritische waarde in de Mann-Whitney U-tabel.
5. Interpreteer de resultaten.
Interpreteer de testresultaten in de context van de gestelde vraag.
Voorbeelden van het uitvoeren van een Mann-Whitney U-test
De volgende voorbeelden laten zien hoe u een Mann-Whitney U-test uitvoert.
voorbeeld 1
We willen weten of een nieuw medicijn effectief is in het voorkomen van paniekaanvallen. In totaal worden twaalf patiënten willekeurig verdeeld in twee groepen van zes en toegewezen aan het nieuwe medicijn of de placebo. Patiënten registreren vervolgens het aantal paniekaanvallen dat ze in de loop van een maand hebben ervaren.
De resultaten worden hieronder weergegeven:
| NIEUW MEDICIJN | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Voer een Mann-Whitney U-test uit om te zien of er een verschil is in het aantal paniekaanvallen onder patiënten in de placebogroep vergeleken met de nieuwe medicijngroep. Gebruik een significantieniveau van 0,05.
1. Geef de aannames weer.
H 0 : De twee populaties zijn gelijk
H a : De twee populaties zijn niet gelijk
2. Bepaal een significantieniveau dat voor de hypothese moet worden gebruikt.
Het probleem vertelt ons dat we een significantieniveau van 0,05 moeten gebruiken.
3. Zoek de teststatistiek.
Bedenk dat de teststatistiek U wordt genoemd en de kleinste is van U 1 en U 2 , zoals hieronder gedefinieerd:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
waarbij n 1 en n 2 de steekproefgroottes zijn voor respectievelijk monsters 1 en 2, en R 1 en R 2 de som zijn van de rangen voor respectievelijk monsters 1 en 2.
Om R 1 en R 2 te vinden, moeten we de waarnemingen van beide groepen combineren en ze ordenen van klein naar groot:
| NIEUW MEDICIJN | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Totaal monster: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Rangen: 1,5 , 1,5 , 3 , 4,5 , 4,5 , 6,5 , 6,5 , 8,5 , 8,5 , 10 , 11 , 12
R 1 = som van de rangen voor steekproef 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = som van de rangen voor monster 2 = 1,5+3+6,5+10+11+12 = 44
Vervolgens gebruiken we onze steekproefomvang n 1 en n 2 en onze rangschikking R 1 en R 2 om U 1 en U 2 te vinden.
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Onze teststatistieken zijn de kleinste van U1 en U2 , wat toevallig U=13 is.
Opmerking: we kunnen ook de Mann-Whitney U-testcalculator gebruiken om te bepalen dat U = 13.
4. Verwerp de nulhypothese of verwerp deze niet.
Door gebruik te maken van n 1 = 6 en n 2 = 6 met een significantieniveau van 0,05, vertelt de Mann-Whitney U-tabel ons dat de kritische waarde 5 is:
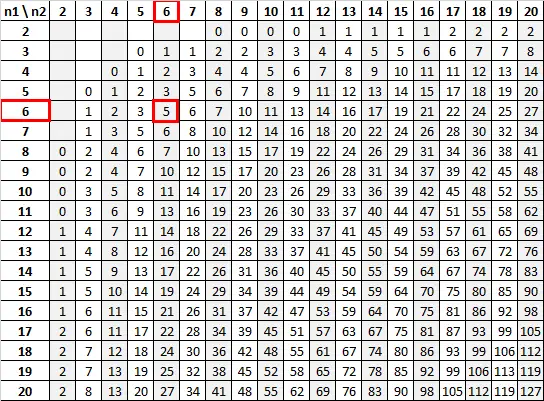
Omdat onze teststatistiek (13) groter is dan onze kritische waarde (5), slagen we er niet in de nulhypothese te verwerpen.
5. Interpreteer de resultaten.
Omdat we er niet in zijn geslaagd de nulhypothese te verwerpen, hebben we niet voldoende bewijs om te zeggen dat het aantal paniekaanvallen dat patiënten in de placebogroep ervaren, anders is dan dat in de nieuwe geneesmiddelengroep.
Voorbeeld 2
We willen weten of studenten een week lang 30 minuten per dag studeren ervoor zorgen dat studenten beter presteren op een toets. In totaal worden 15 patiënten willekeurig toegewezen aan een onderzoeksgroep of geen onderzoeksgroep. Na een week maken alle leerlingen dezelfde toets.
De testresultaten voor beide groepen worden hieronder weergegeven:
| STUDIE | GEEN STUDIE |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Voer een Mann-Whitney U-test uit om te zien of er een verschil is in de testscores voor de onderzoeksgroep vergeleken met de groep zonder onderzoek. Gebruik een significantieniveau van 0,01.
1. Geef de aannames weer.
H 0 : De twee populaties zijn gelijk
H a : De twee populaties zijn niet gelijk
2. Bepaal een significantieniveau dat voor de hypothese moet worden gebruikt.
Het probleem vertelt ons dat we een significantieniveau van 0,01 moeten gebruiken.
3. Zoek de teststatistiek.
Bedenk dat de teststatistiek U wordt genoemd en de kleinste is van U 1 en U 2 , zoals hieronder gedefinieerd:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
waarbij n 1 en n 2 de steekproefgroottes zijn voor respectievelijk monsters 1 en 2, en R 1 en R 2 de som zijn van de rangen voor respectievelijk monsters 1 en 2.
Om R 1 en R 2 te vinden, moeten we de waarnemingen van beide groepen combineren en ze ordenen van klein naar groot:
| STUDIE | GEEN STUDIE |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Totaal monster: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Rijen: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = som van de rangen voor monster 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = som van de rangen voor monster 2 = 1+2+3+4+6+11+13 = 40
Vervolgens gebruiken we onze steekproefomvang n 1 en n 2 en onze rangschikking R 1 en R 2 om U 1 en U 2 te vinden.
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Onze teststatistieken zijn de kleinste van U1 en U2 , wat toevallig U=12 is.
Opmerking: we kunnen ook de Mann-Whitney U-testcalculator gebruiken om te bepalen dat U = 12.
4. Verwerp de nulhypothese of verwerp deze niet.
Gebruikmakend van n 1 = 8 en n 2 = 7 met een significantieniveau van 0,01, vertelt de Mann-Whitney U-tabel ons dat de kritische waarde 6 is:
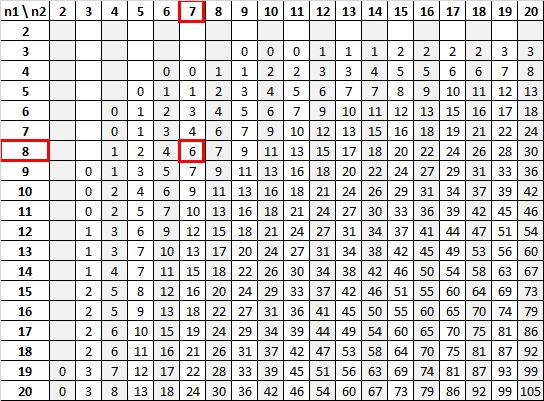
Omdat onze teststatistiek (12) groter is dan onze kritische waarde (6), slagen we er niet in de nulhypothese te verwerpen.
5. Interpreteer de resultaten.
Omdat we er niet in zijn geslaagd de nulhypothese te verwerpen, hebben we niet voldoende bewijs om te zeggen dat de toetsscores van studenten die wel studeerden anders zijn dan die van studenten die niet studeerden.
Aanvullende bronnen
Mann-Whitney U-testcalculator
Mann-Whitney U-tafel
Hoe u een Mann-Whitney U-test uitvoert in Excel
Hoe voer je een Mann-Whitney U-test uit in R
Hoe u een Mann-Whitney U-test uitvoert in Python
Hoe u een Mann-Whitney U-test uitvoert in SPSS
Een Mann-Whitney U-test uitvoeren in Stata
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder