De complete gids: manova-aannames controleren

Een MANOVA (multivariate variantieanalyse) wordt gebruikt om te analyseren hoe een of meer factorvariabelen meerdere responsvariabelen beïnvloeden.

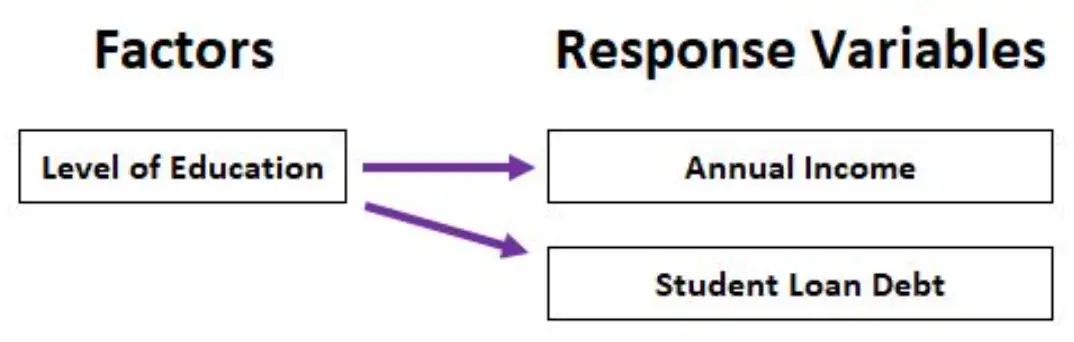
We zouden bijvoorbeeld een MANOVA kunnen gebruiken om te analyseren hoe het opleidingsniveau (middelbareschooldiploma, universitair diploma, bachelordiploma, masterdiploma) zowel het jaarinkomen als de totale studieschuld beïnvloedt.

Gerelateerd: De verschillen tussen ANOVA, ANCOVA, MANOVA en MANCOVA

Elke keer dat we een MANOVA uitvoeren, moeten we verifiëren dat aan de volgende aannames wordt voldaan:

1. Multivariate normaliteit – De responsvariabelen zijn multivariate normaal verdeeld binnen elke groep factorvariabelen.

2. Onafhankelijkheid – Elke waarneming wordt willekeurig en onafhankelijk uit de populatie getrokken.

3. Gelijke variantie – De populatiecovariantiematrices van elke groep zijn gelijk.

4. Geen multivariate uitschieters – Er zijn geen extreme multivariate uitschieters.

In dit artikel geven we een uitleg van elke aanname en hoe je kunt bepalen of aan de aanname is voldaan.

Aanname 1: Multivariate normaliteit

Een MANOVA gaat ervan uit dat de responsvariabelen multivariabel zijn en normaal verdeeld zijn binnen elke groep van de factorvariabele.

Als er voor elke combinatie van factor * responsvariabelen ten minste 20 waarnemingen zijn, kunnen we aannemen dat aan de aanname van multivariate normaliteit is voldaan.

Als er minder dan 20 waarnemingen zijn voor elke combinatie van factor*responsvariabelen, kunnen we een spreidingsdiagrammatrix maken om de residuen te visualiseren en visueel te controleren of aan deze aanname wordt voldaan.

Gelukkig is het algemeen bekend dat MANOVA robuust is tegen afwijkingen van de multivariate normaliteit, dus kleine tot matige afwijkingen zijn over het algemeen geen probleem.

Hypothese 2: Onafhankelijkheid

Een MANOVA gaat ervan uit dat elke waarneming willekeurig en onafhankelijk uit de populatie wordt getrokken.

Zolang een probabiliteitssteekproefmethode (elk lid van een populatie heeft een gelijke kans om geselecteerd te worden om in de steekproef opgenomen te worden) wordt gebruikt om de gegevens te verzamelen, kunnen we ervan uitgaan dat elke waarneming op een willekeurige en onafhankelijke manier is bemonsterd.

Voorbeelden van waarschijnlijkheidssteekproefmethoden zijn onder meer:

• Eenvoudige willekeurige steekproef
• Gestratificeerde willekeurige steekproeven
• Willekeurige clusterbemonstering
• Systematische willekeurige steekproeven

Aanname 3: gelijke variantie

Een MANOVA gaat ervan uit dat de populatiecovariantiematrices van elke groep gelijk zijn.

De meest gebruikelijke manier om deze hypothese te testen is door de M-test van Box te gebruiken. Het is bekend dat deze test behoorlijk streng is. Daarom gebruiken we doorgaans een significantieniveau van 0,001 om te bepalen of de populatiecovariantiematrices gelijk zijn of niet.

Als de p-waarde van Box’s M-test groter is dan 0,001, kunnen we aannemen dat aan deze veronderstelling is voldaan.

Gelukkig is een MANOVA, zelfs als de p-waarde van de test kleiner is dan 0,001, doorgaans robuust tegen afwijkingen van deze hypothese.

Om niet-gelijke covariantiematrices een probleem te laten zijn, moeten de verschillen tussen de covariantiematrices behoorlijk extreem zijn.

Hypothese 4: geen multivariate uitbijters

Een MANOVA gaat ervan uit dat er geen extreme multivariate uitschieters in de gegevens aanwezig zijn die de resultaten aanzienlijk kunnen beïnvloeden.

De meest gebruikelijke manier om deze aanname te verifiëren is door voor elke waarneming de Mahalanobis-afstand te berekenen, die de afstand tussen twee punten in een multivariate ruimte vertegenwoordigt.

Als de overeenkomstige p-waarde voor een Mahalanobis-afstand van een waarneming kleiner is dan 0,001, beschouwen we die waarneming doorgaans als een extreme uitbijter.

Raadpleeg de volgende tutorials om te zien hoe u de Mahalanobis-afstand in verschillende statistische software kunt berekenen:

• Hoe de Mahalanobis-afstand in R te berekenen
• Hoe de Mahalanobis-afstand in SPSS te berekenen
• Hoe Mahalanobis-afstand in Python te berekenen

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een MANOVA uitvoert in verschillende statistische software:

Hoe voer je een MANOVA uit in R
Hoe u een MANOVA uitvoert in SPSS
Hoe voer je een MANOVA uit in Stata