Hoe voer je een manova uit in stata

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of verschillende niveaus van een verklarende variabele al dan niet tot statistisch verschillende resultaten leiden bij bepaalde responsvariabelen.

We zouden bijvoorbeeld graag willen weten of drie onderwijsniveaus (associategraad, bachelorgraad, mastergraad) al dan niet tot statistisch verschillende jaarlijkse inkomsten leiden. In dit geval hebben we een verklarende variabele en een responsvariabele.

• Verklarende variabele: opleidingsniveau
• Responsvariabele: jaarinkomen

Een MANOVA is een uitbreiding van een eenrichtings-ANOVA waarbij er meer dan één responsvariabele is. We zouden bijvoorbeeld graag willen weten of het opleidingsniveau al dan niet leidt tot verschillende jaarinkomens en verschillende bedragen aan studieschulden. In dit geval hebben we één verklarende variabele en twee responsvariabelen:

• Verklarende variabele: opleidingsniveau
• Responsvariabelen: jaarinkomen, studieschuld

Omdat we meer dan één responsvariabele hebben, zou het in dit geval passend zijn om een MANOVA te gebruiken.

Vervolgens leggen we uit hoe u een MANOVA uitvoert in Stata.

Voorbeeld: MANOVA in Stata

Om te illustreren hoe je een MANOVA in Stata uitvoert, zullen we de volgende dataset gebruiken die de volgende drie variabelen bevat voor 24 personen:

• educ: studieniveau (0 = Associate, 1 = Bachelor, 2 = Master)
• inkomen: jaarinkomen
• schuld: totale studieschuld

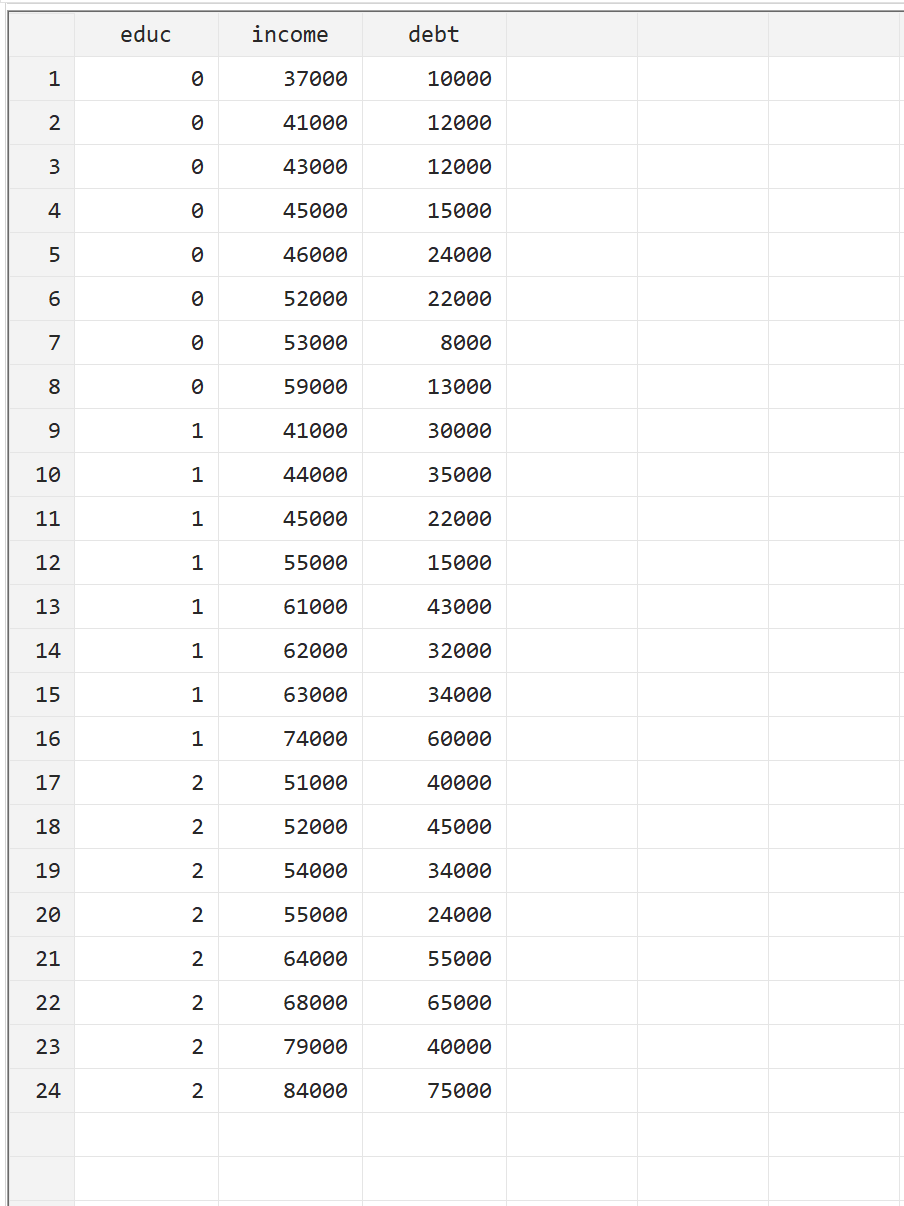
U kunt dit voorbeeld reproduceren door de gegevens zelf handmatig in te voeren door naar Gegevens > Gegevenseditor > Gegevenseditor (Bewerken) in de bovenste menubalk te navigeren.

Om de MANOVA uit te voeren met onderwijs als verklarende variabele en inkomen en schuld als antwoordvariabelen, kunnen we het volgende commando gebruiken:

inkomensschuld manova = onderwijs

Stata produceert vier unieke teststatistieken samen met de bijbehorende p-waarden:

Wilks‘ lambda: F-statistiek = 5,02, P-waarde = 0,0023.

Pillai-trace: F-statistiek = 4,07, P-waarde = 0,0071.

Lawley-Hotelling-trace: F-statistiek = 5,94, P-waarde = 0,0008.

Grootste Roy-wortel: F-statistiek = 13,10, P-waarde = 0,0002.

Voor een gedetailleerde uitleg over hoe elke teststatistiek wordt berekend, raadpleegt u dit artikel van het Penn State Eberly College of Science.

De p-waarde voor elke teststatistiek is kleiner dan 0,05, dus de nulhypothese wordt verworpen, ongeacht welke je gebruikt. Dit betekent dat we voldoende bewijs hebben om te zeggen dat het opleidingsniveau statistisch significante verschillen veroorzaakt in het jaarinkomen en de totale studieschuld.

Opmerking over p-waarden: De letter naast de p-waarde in de uitvoertabel geeft aan hoe de F-statistiek werd berekend (e = exacte berekening, a = geschatte berekening, u = bovengrens).