Prioriteringsmatrix (of prioriteitenmatrix)

In dit artikel wordt uitgelegd wat een prioriteringsmatrix, ook wel prioriteitenmatrix genoemd, is, wat de kenmerken ervan zijn en waarvoor deze wordt gebruikt. Op dezelfde manier kunt u zien hoe u een prioriteringsmatrix kunt maken en bovendien een voorbeeld dat stap voor stap wordt uitgelegd.

Wat is een prioriteitenmatrix?

Een prioriteringsmatrix (of prioriteitenmatrix ) is een matrix waarmee u verschillende opties kunt vergelijken op basis van verschillende criteria. Daarom wordt een prioriteringsmatrix gebruikt om verschillende opties te evalueren en er objectief één te kiezen.

Dat wil zeggen dat in een prioriteringsmatrix de verschillende beschikbare opties worden geclassificeerd op basis van de score die is behaald op basis van de eerder gekozen criteria, zodat een beslissing kan worden genomen op basis van een objectieve methode.

Normaal gesproken is elke rij van de matrix een optie waaruit u kunt kiezen, terwijl de kolommen van de matrix de selectiecriteria vertegenwoordigen. Het vak waar een rij en een kolom elkaar kruisen, is dus de score die deze optie op dit criterium krijgt.

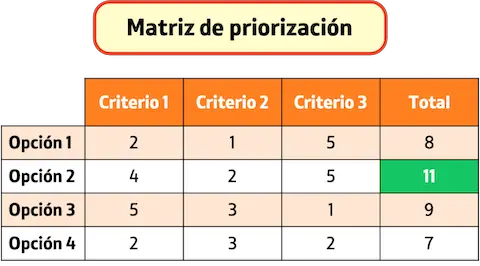
De prioriteringsmatrix wordt ook wel een multicriteriamatrix of een prioriteringsdiagram genoemd.

Hoe maak je een prioriteitenmatrix?

De stappen voor het maken van een prioriteitenmatrix zijn als volgt:

1. Definieer het doel van de prioriteitenmatrix : Voordat u begint met het maken van de prioriteitenmatrix, moet het doel van het maken van de matrix duidelijk zijn. Op deze manier wordt het gemakkelijker om de criteria te kiezen.
2. Identificeer opties : Maak een lijst van alle mogelijke opties die moeten worden geëvalueerd. In sommige gevallen zullen de opties al gedefinieerd zijn, in andere gevallen zul je vindingrijk moeten zijn en met alternatieven moeten komen.
3. Stel criteria vast : De gekozen criteria om de verschillende opties te scoren moeten aansluiten bij het doel van de prioriteringsmatrix. Daarom is het belangrijk om het doel van de matrix duidelijk te definiëren. Bovendien hoeven alleen de voor het project relevante criteria te worden ingevuld; te veel criteria kunnen ertoe leiden dat de gekozen optie niet de meest geschikte is.
4. Weging van de criteria : zodra de verschillende criteria zijn gedefinieerd, moeten ze worden gewogen op basis van het belang van elk ervan. Normaal gesproken gebeurt dit als een percentage, zodat het belangrijkste criterium overeenkomt met een hoger percentage en de som van alle gewichten 1 (of 100%) oplevert.
5. Evalueer de opties – Elke optie moet voor elk criterium een score krijgen. Het wordt aanbevolen dat het bereik van alle scores hetzelfde is, omdat het verschil in belangrijkheid van de criteria al wordt vastgesteld door de gewichten.
6. Selecteer de beste optie : Nadat alle opties voor elk criterium zijn beoordeeld, worden alle ontvangen scores bij elkaar opgeteld. De beste optie is, in theorie, degene met de meeste punten.

Voorbeeld van een prioriteringsmatrix

Nadat we de definitie van de prioriteringsmatrix hebben gezien en hoe deze wordt uitgevoerd, zullen we een stapsgewijs voorbeeld zien om het concept te verwerken.

• Een bank wil investeren door een klein bedrijf te kopen met als doel het te laten groeien en het vervolgens tegen een hogere prijs door te verkopen. Nadat ze verschillende economische filters hebben doorstaan, zijn de bedrijven die een aankoop overwegen bedrijf A, bedrijf B en bedrijf C.

Om te analyseren welk bedrijf het beste door de bank kan worden gekocht, zullen we een prioriteringsmatrix opstellen. In dit geval kennen we het doel en de verschillende opties van de matrix al:

Doel: Koop een klein bedrijf om het na een tijdje voor meer geld door te verkopen en de investering winstgevend te maken.

Mogelijkheden:

• Optie 1: Bedrijf A
• Optie 2: Bedrijf B
• Optie 3: Bedrijf C

Om de verschillende opties te beoordelen, gebruiken we de volgende selectiecriteria:

Criteria:

• Criterium 1: Aankoopprijs. Logischerwijs geldt: hoe lager de overnameprijs van het bedrijf, hoe meer de bank hiervan profiteert, omdat er minder geld wordt uitgegeven.
• Criterium 2: Groeipotentieel. Er moet rekening worden gehouden met het groeipotentieel en de waardestijging van het bedrijf, omdat de bank hierdoor een groter economisch rendement behaalt.
• Criterium 3: Risico op faillissement. Er moet ook rekening worden gehouden met het risico dat elk bedrijf failliet gaat, omdat de bank in dit geval al het geïnvesteerde geld zou verliezen. Hoe hoger de score op dit criterium, hoe lager het risico op sluiting van het bedrijf.
• Criterium 4: Jaarwinst van de onderneming. De jaarlijkse winst van het bedrijf moet ook worden gewaardeerd, aangezien het om extra geld gaat dat de bank zou verdienen naast de winst uit de aan- en verkoop van het bedrijf.

Nu we weten welke criteria we zullen gebruiken in de prioriteringsmatrix, wegen we ze op basis van hun relevantie.

Criteriawegingen:

• Criterium 1: Aankoopprijs → 30%
• Criterium 2: Groeipotentieel → 40%
• Criterium 3: Risico op faillissement → 20%
• Criterium 4: Jaarwinst van het bedrijf → 10%

Nadat we de criteria hebben gewogen, stellen we de prioriteringsmatrix op basis van beoordeling op. Om dit te doen, werd elke optie voor elk criterium beoordeeld van 1 tot 10 en vervolgens werden de scores opgeteld volgens de wegingen van de criteria.

Evalueer de opties en kies de beste:

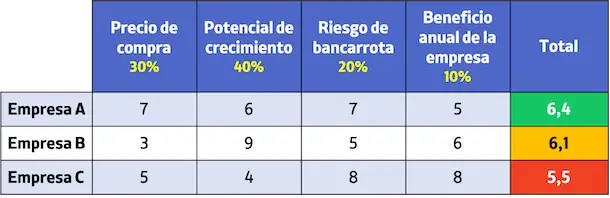
Concluderend zou de bank, na elk van de bedrijven te hebben beoordeeld aan de hand van de verschillende vastgestelde criteria, bedrijf A moeten kopen, aangezien dit het bedrijf is dat de beste score heeft behaald.

Waar wordt een prioriteringsmatrix voor gebruikt?

Hieronder geven wij u een samenvatting waarvoor het nuttig is en wanneer u de prioriteringsmatrix kunt gebruiken.

• Identificeer beslissingscriteria – Door de selectiecriteria te bepalen, kunt u zien wat het belangrijkste is voor het project en waarop de beslissing moet worden gebaseerd.
• Probleemverduidelijking : Door de beslissingscriteria te kiezen, krijgt u een duidelijker beeld van het echte probleem waarmee u wordt geconfronteerd en van de belangrijkste aspecten om het op te lossen.
• Analyse van opties : de prioriteitenmatrix vergemakkelijkt de analyse van alle opties, omdat deze een snelle visualisatie van de score van elke optie op elk criterium mogelijk maakt.
• Zoeken naar verbetermogelijkheden : bij het uitvoeren van de prioriteringsmatrix kunt u concluderen dat één optie de beste is voor uw project of, integendeel, dat u nieuwe opties moet onderzoeken die de resultaten uit de matrix verbeteren.

Voor- en nadelen van de prioriteringsmatrix

Voordeel:

• De prioriteringsmatrix is een eenvoudig te gebruiken hulpmiddel. Bovendien kunnen opties, criteria of wegingen snel worden bijgewerkt en aangepast.
• Het is erg handig voor projectbeheer, omdat u hiermee meerdere opties kunt analyseren en kunt beslissen welke de beste is, waardoor u tijd bespaart.
• Dit is een objectieve methode, zodat eventuele vooroordelen van een persoon worden verminderd.
• De prioriteringsmatrix is heel eenvoudig te begrijpen, zowel voor degenen die hem uitvoeren als voor degenen die hem interpreteren.

Nadelen:

• Het behaalde resultaat hangt volledig af van de zelfbeoordeling van de criteria en hun wegingen, het team moet dus neutraal blijven.
• Afhankelijk van het type organisatie kan de prioriteitenmatrix te rigide worden.
• Soms scoren twee of meer opties zeer vergelijkbaar, waardoor het onduidelijk is welke beslissing moet worden genomen. In dit geval wordt aanbevolen om de prioriteitenmatrix opnieuw uit te voeren met andere criteria en gewichten.