Een verwarringsmatrix creëren in r (stap voor stap)

Logistische regressie is een type regressie dat we kunnen gebruiken als de responsvariabele binair is.

Een gebruikelijke manier om de kwaliteit van een logistisch regressiemodel te beoordelen, is door een verwarringsmatrix te maken, een tabel van 2 × 2 die de voorspelde waarden van het model weergeeft versus de werkelijke waarden van de testdataset.

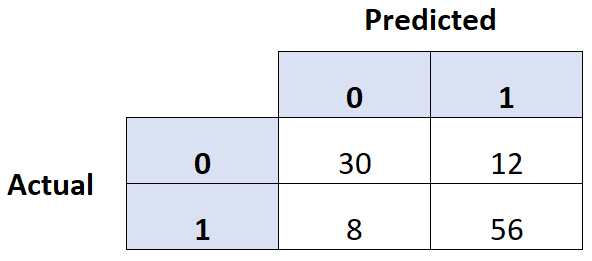
Het volgende stapsgewijze voorbeeld laat zien hoe u een verwarringsmatrix in R maakt.

Stap 1: Pas het logistische regressiemodel toe

Voor dit voorbeeld gebruiken we de standaarddataset uit het ISLR- pakket. We zullen de studentenstatus, het banksaldo en het jaarinkomen gebruiken om de waarschijnlijkheid te voorspellen dat een bepaalde persoon zijn lening niet kan afbetalen.

De volgende code laat zien hoe u een logistisch regressiemodel aan deze gegevensset kunt aanpassen:

 #load necessary packages
library (caret)
library (InformationValue)
library (ISLR)

#load dataset
data <-Default

#split dataset into training and testing set
set. seeds (1)
sample <- sample(c(TRUE, FALSE), nrow(data), replace= TRUE , prob=c(0.7,0.3))
train <- data[sample, ]
test <- data[!sample, ]

#fit logistic regression model
model <- glm(default~student+balance+income, family=" binomial ", data=train)

Stap 2: Creëer de verwarringsmatrix

Vervolgens zullen we de functie verwarringMatrix() uit het dakje- pakket gebruiken om een verwarringsmatrix te maken:

 #use model to predict probability of default
predicted <- predict(model, test, type="response")

#convert defaults from "Yes" and "No" to 1's and 0's
test$default <- ifelse(test$default==" Yes ", 1, 0)

#find optimal cutoff probability to use to maximize accuracy
optimal <- optimalCutoff(test$default, predicted)[1]

#create confusion matrix
confusionMatrix(test$default, predicted)

     0 1
0 2912 64
1 21 39

Stap 3: Evalueer de verwarringsmatrix

We kunnen ook de volgende statistieken berekenen met behulp van de verwarringsmatrix:

• Gevoeligheid: Het ‘echte positiviteitspercentage’ – het percentage individuen waarvan het model correct voorspelde dat ze in gebreke zouden blijven.
• Specificiteit: Het “echte negatieve percentage” – het percentage individuen waarvan het model correct voorspelde dat ze niet in gebreke zouden blijven.
• Totaal percentage misclassificaties: percentage van het totale aantal misclassificaties dat door het model is gemaakt.

De volgende code laat zien hoe u deze statistieken berekent:

 #calculate sensitivity
sensitivity(test$default, predicted)

[1] 0.3786408

#calculate specificity
specificity(test$default, predicted)

[1] 0.9928401

#calculate total misclassification error rate
misClassError(test$default, predicted, threshold =optimal)

[1] 0.027

Het totale classificatiefoutenpercentage bedraagt voor dit model 2,7% .

Over het algemeen geldt: hoe lager dit percentage, hoe beter het model de resultaten kan voorspellen. Dit specifieke model blijkt daarom zeer effectief te zijn bij het voorspellen of een individu in gebreke zal blijven of niet.