Meervoudige lineaire regressie met de hand (stap voor stap)
Meervoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen twee of meer voorspellende variabelen en een responsvariabele te kwantificeren.
In deze zelfstudie wordt uitgelegd hoe u handmatig meerdere lineaire regressies uitvoert.
Voorbeeld: meervoudige lineaire regressie met de hand
Stel dat we de volgende gegevensset hebben met een responsvariabele y en twee voorspellende variabelen x 1 en x 2 :
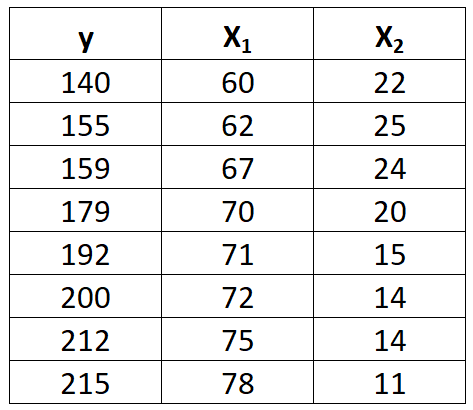
Voer de volgende stappen uit om een meervoudig lineair regressiemodel aan deze gegevensset toe te passen.
Stap 1: Bereken x 1 2 , x 2 2 , x 1 y, x 2 y en x 1 x 2 .
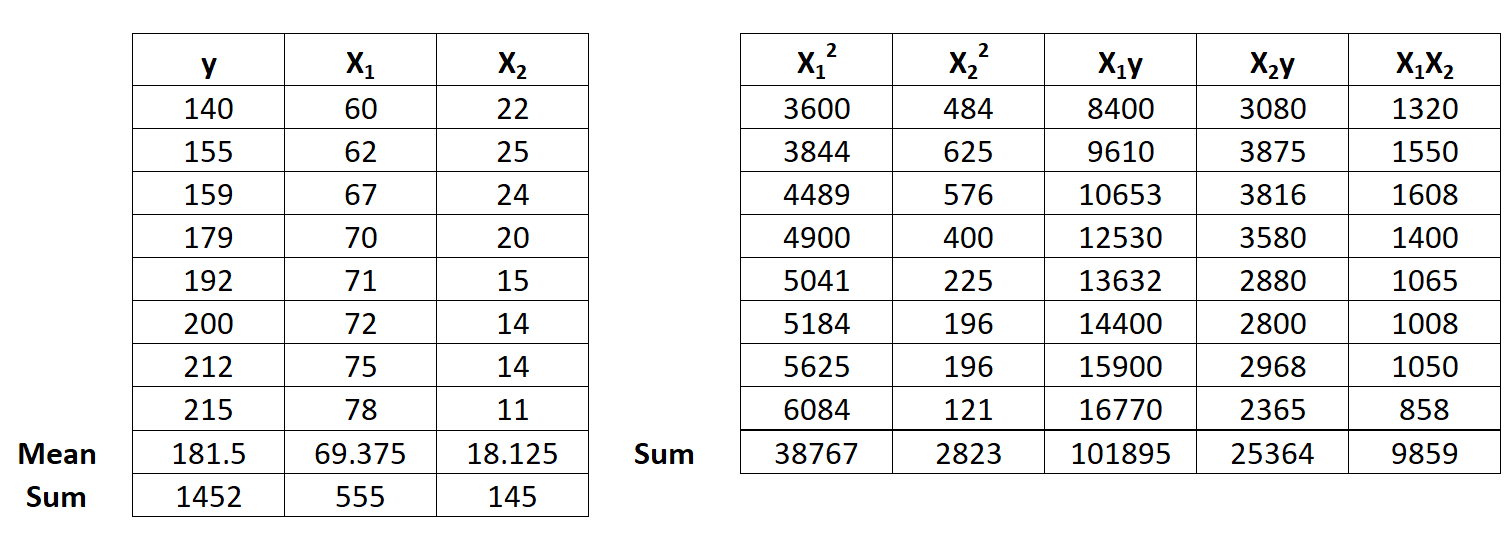
Stap 2: Bereken de regressiesommen.
Voer vervolgens de volgende regressiesomberekeningen uit:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2 / 8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
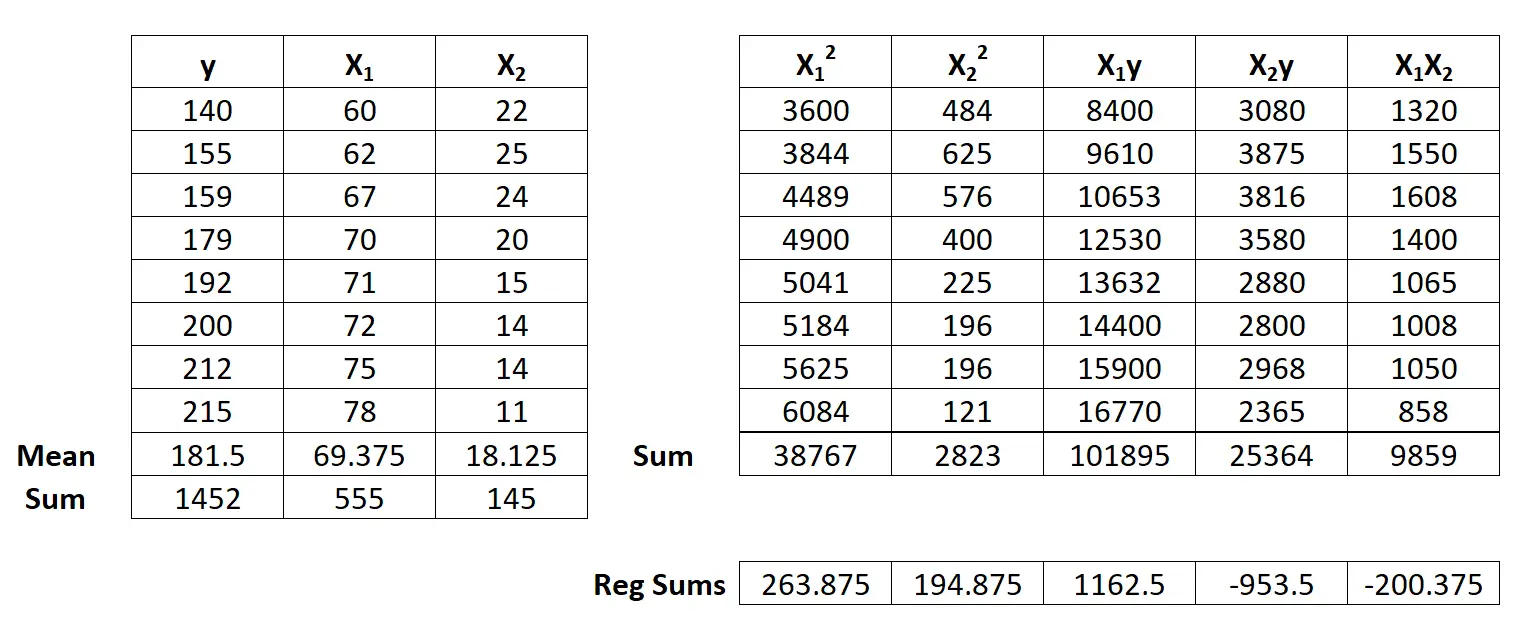
Stap 3: Bereken b 0 , b 1 en b 2 .
De formule om b 1 te berekenen is: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Dus b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
De formule om b 2 te berekenen is: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Dus b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
De formule om b 0 te berekenen is: y – b 1 X 1 – b 2 X 2
Dus b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Stap 5: Plaats b 0 , b 1 en b 2 in de geschatte lineaire regressievergelijking.
De geschatte lineaire regressievergelijking is: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
In ons voorbeeld is dit ŷ = -6,867 + 3,148x 1 – 1,656x 2
Hoe een meervoudige lineaire regressievergelijking te interpreteren
Zo interpreteert u deze geschatte lineaire regressievergelijking: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Wanneer beide voorspellende variabelen gelijk zijn aan nul, is de gemiddelde waarde van y -6,867.
b1 = 3,148 . Een toename van één eenheid in x 1 gaat gepaard met een gemiddelde toename van 3,148 eenheden in y, ervan uitgaande dat x 2 constant blijft.
b2 = -1,656 . Een toename van één eenheid in x 2 gaat gepaard met een afname van y met gemiddeld 1.656 eenheden, ervan uitgaande dat x 1 constant blijft.
Aanvullende bronnen
Een inleiding tot meervoudige lineaire regressie
Hoe u eenvoudige lineaire regressie met de hand kunt uitvoeren
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder