De vijf aannames van meervoudige lineaire regressie
Meervoudige lineaire regressie is een statistische methode die we kunnen gebruiken om de relatie tussen meerdere voorspellende variabelen en eenresponsvariabele te begrijpen.
Voordat we echter meervoudige lineaire regressie uitvoeren, moeten we er eerst voor zorgen dat aan vijf aannames wordt voldaan:
1. Lineair verband: Er bestaat een lineair verband tussen elke voorspellende variabele en de responsvariabele.
2. Geen multicollineariteit: geen van de voorspellende variabelen is sterk met elkaar gecorreleerd.
3. Onafhankelijkheid: De waarnemingen zijn onafhankelijk.
4. Homoscedasticiteit: de residuen hebben een constante variantie op elk punt van het lineaire model.
5. Multivariate normaliteit: De modelresiduen zijn normaal verdeeld.
Als aan een of meer van deze aannames niet wordt voldaan, zijn de resultaten van meervoudige lineaire regressie mogelijk niet betrouwbaar.
In dit artikel geven we een uitleg voor elke aanname, hoe je kunt bepalen of aan de aanname wordt voldaan en wat je moet doen als niet aan de aanname wordt voldaan.
Hypothese 1: Lineair verband
Bij meervoudige lineaire regressie wordt ervan uitgegaan dat er een lineair verband bestaat tussen elke voorspellende variabele en de responsvariabele.
Hoe te bepalen of aan deze veronderstelling wordt voldaan
De eenvoudigste manier om te bepalen of aan deze veronderstelling wordt voldaan, is door een spreidingsdiagram te maken van elke voorspellende variabele en de responsvariabele.
Hiermee kunt u visueel zien of er een lineair verband bestaat tussen de twee variabelen.
Als de punten in het spreidingsdiagram ongeveer langs een rechte diagonale lijn liggen, is er waarschijnlijk een lineair verband tussen de variabelen.
De punten in de onderstaande grafiek lijken bijvoorbeeld op een rechte lijn te vallen, wat aangeeft dat er een lineair verband bestaat tussen deze specifieke voorspellende variabele (x) en de responsvariabele (y):
Wat te doen als deze veronderstelling niet wordt gerespecteerd
Als er geen lineair verband bestaat tussen een of meer voorspellende variabelen en de responsvariabele, dan hebben we verschillende opties:
1. Pas een niet-lineaire transformatie toe op de voorspellende variabele, bijvoorbeeld door de logaritmische of vierkantswortel te nemen. Dit kan de relatie vaak een meer lineaire relatie maken.
2. Voeg nog een voorspellende variabele toe aan het model. Als de grafiek van x versus y bijvoorbeeld een parabolische vorm heeft, kan het zinvol zijn om X 2 toe te voegen als extra voorspellende variabele in het model.
3. Verwijder de voorspellende variabele uit het model. In het meest extreme geval, als er geen lineair verband bestaat tussen een bepaalde voorspellende variabele en de responsvariabele, is het wellicht niet zinvol om de voorspellende variabele in het model op te nemen.
Hypothese 2: geen multicollineariteit
Bij meervoudige lineaire regressie wordt ervan uitgegaan dat geen van de voorspellende variabelen sterk met elkaar gecorreleerd is.
Wanneer een of meer voorspellende variabelen sterk gecorreleerd zijn, lijdt het regressiemodel aan multicollineariteit , waardoor de coëfficiëntschattingen van het model onbetrouwbaar worden.
Hoe te bepalen of aan deze veronderstelling wordt voldaan
De eenvoudigste manier om te bepalen of aan deze veronderstelling wordt voldaan, is door de VIF-waarde voor elke voorspellende variabele te berekenen.
VIF-waarden beginnen bij 1 en hebben geen bovengrens. Over het algemeen duiden VIF-waarden boven 5* op potentiële multicollineariteit.
De volgende tutorials laten zien hoe u VIF in verschillende statistische software kunt berekenen:
*Soms gebruiken onderzoekers in plaats daarvan een VIF-waarde van 10, afhankelijk van het vakgebied.
Wat te doen als deze veronderstelling niet wordt gerespecteerd
Als een of meer voorspellende variabelen een VIF-waarde groter dan 5 hebben, is de eenvoudigste manier om dit probleem op te lossen het simpelweg verwijderen van de voorspellende variabelen met de hoge VIF-waarden.
Als u elke voorspellende variabele in het model wilt behouden, kunt u ook een andere statistische methode gebruiken, zoals ridge regressie , lasso regressie of gedeeltelijke kleinste kwadraten regressie , die is ontworpen om sterk gecorreleerde voorspellende variabelen te verwerken.
Hypothese 3: Onafhankelijkheid
Bij meervoudige lineaire regressie wordt ervan uitgegaan dat elke waarneming in de dataset onafhankelijk is.
Hoe te bepalen of aan deze veronderstelling wordt voldaan
De eenvoudigste manier om te bepalen of aan deze veronderstelling wordt voldaan, is door een Durbin-Watson-test uit te voeren, een formele statistische test die ons vertelt of de residuen (en dus de waarnemingen) al dan niet autocorrelatie vertonen.
Wat te doen als deze veronderstelling niet wordt gerespecteerd
Afhankelijk van hoe deze veronderstelling wordt geschonden, hebt u verschillende opties:
- Voor positieve seriële correlatie kunt u overwegen vertragingen van de afhankelijke en/of onafhankelijke variabele aan het model toe te voegen.
- Zorg er bij negatieve seriële correlatie voor dat geen van uw variabelen te veel vertraging heeft.
- Voor seizoenscorrelatie kunt u overwegen seizoensdummies aan het model toe te voegen.
Hypothese 4: homoscedasticiteit
Bij meervoudige lineaire regressie wordt ervan uitgegaan dat de residuen op elk punt in het lineaire model een constante variantie hebben. Wanneer dit niet het geval is, lijden de residuen aan heteroscedasticiteit .
Wanneer heteroscedasticiteit aanwezig is in een regressieanalyse, worden de resultaten van het regressiemodel onbetrouwbaar.
Concreet vergroot heteroskedasticiteit de variantie van de schattingen van de regressiecoëfficiënten, maar het regressiemodel houdt daar geen rekening mee. Dit maakt het veel waarschijnlijker dat een regressiemodel zal beweren dat een term in het model statistisch significant is, terwijl dat in werkelijkheid niet het geval is.
Hoe te bepalen of aan deze veronderstelling wordt voldaan
De eenvoudigste manier om te bepalen of aan deze veronderstelling wordt voldaan, is door een grafiek te maken van de gestandaardiseerde residuen tegen de voorspelde waarden.
Zodra u een regressiemodel aan een gegevensset heeft aangepast, kunt u een spreidingsdiagram maken dat de voorspelde waarden van de responsvariabele op de x-as en de gestandaardiseerde residuen van het model op de x-as weergeeft. j.
Als de punten in het spreidingsdiagram een trend vertonen, is er sprake van heteroscedasticiteit.
Het volgende diagram toont een voorbeeld van een regressiemodel waarin heteroskedasticiteit geen probleem is:
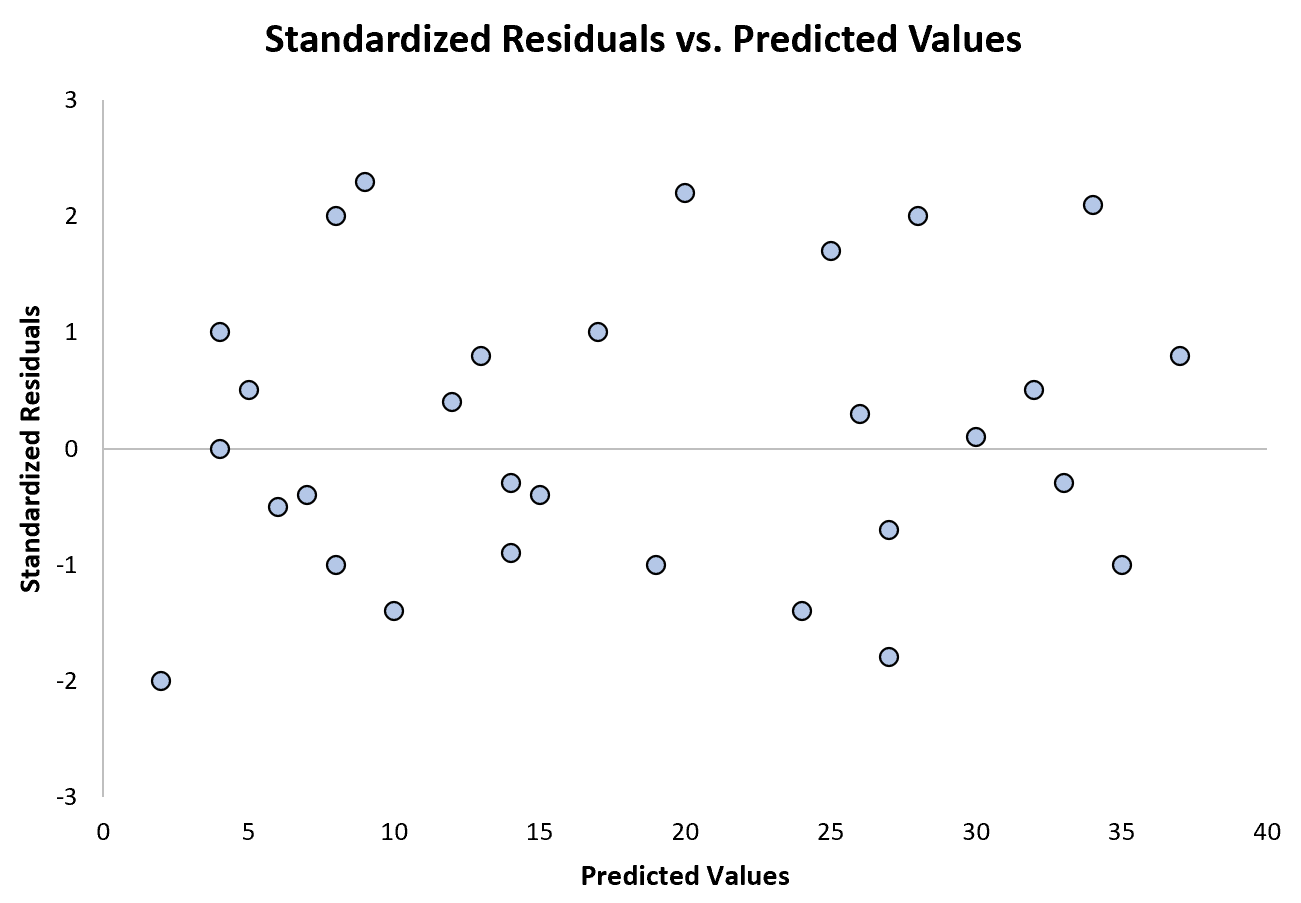
Merk op dat de gestandaardiseerde residuen rond nul verspreid zijn, zonder duidelijk patroon.
Het volgende diagram toont een voorbeeld van een regressiemodel waarbij heteroscedasticiteit een probleem is :
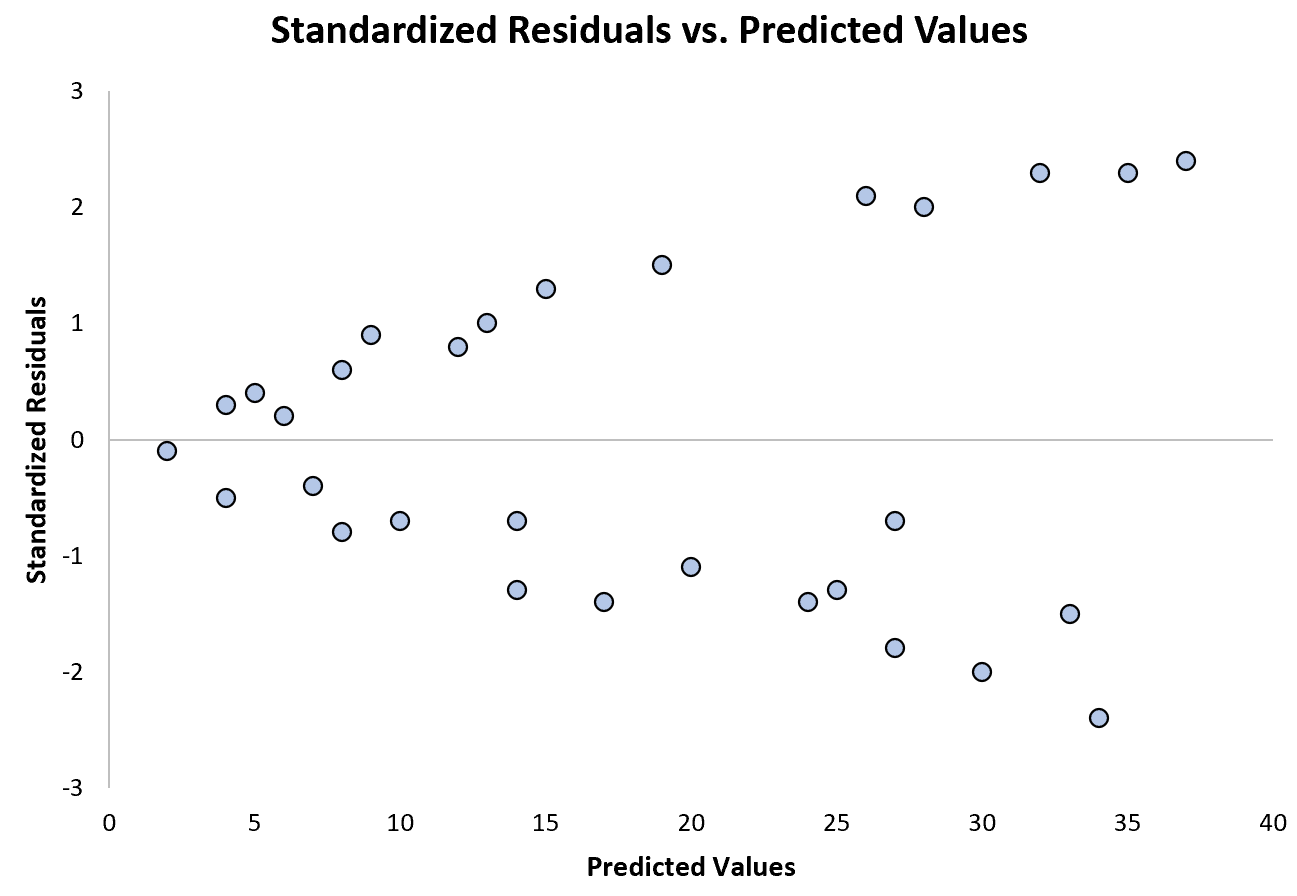
Merk op hoe de gestandaardiseerde residuen zich steeds verder verspreiden naarmate de voorspelde waarden toenemen. Deze “kegelvorm” is een klassiek teken van heteroscedasticiteit:
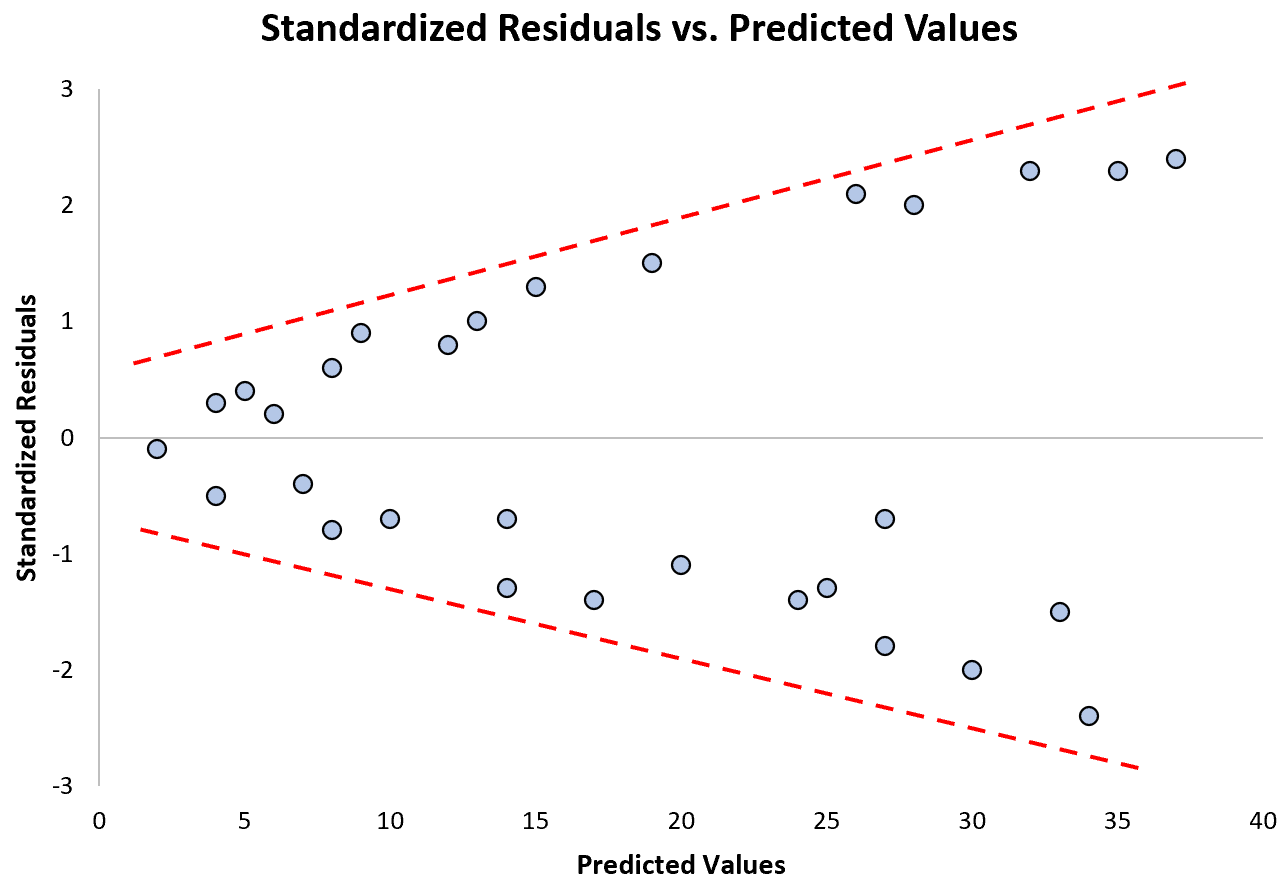
Wat te doen als deze veronderstelling niet wordt gerespecteerd
Er zijn drie veelgebruikte manieren om heteroskedasticiteit te corrigeren:
1. Transformeer de responsvariabele. De meest gebruikelijke manier om met heteroskedasticiteit om te gaan, is door de responsvariabele te transformeren door de log-, vierkantswortel of derdemachtswortel te nemen van alle waarden van de responsvariabele. Dit resulteert vaak in het verdwijnen van heteroskedasticiteit.
2. Definieer de responsvariabele opnieuw. Eén manier om de responsvariabele opnieuw te definiëren is door een snelheid te gebruiken in plaats van de ruwe waarde. In plaats van de bevolkingsomvang te gebruiken om het aantal bloemisten in een stad te voorspellen, kunnen we bijvoorbeeld de bevolkingsomvang gebruiken om het aantal bloemisten per hoofd van de bevolking te voorspellen.
In de meeste gevallen vermindert dit de variabiliteit die van nature voorkomt binnen grotere populaties, omdat we het aantal bloemisten per persoon meten, in plaats van het aantal bloemisten zelf.
3. Gebruik gewogen regressie. Een andere manier om te corrigeren voor heteroscedasticiteit is het gebruik van gewogen regressie, waarbij aan elk gegevenspunt een gewicht wordt toegekend op basis van de variantie van de aangepaste waarde.
In wezen geeft dit een laag gewicht aan datapunten met hogere varianties, waardoor hun resterende kwadraten kleiner worden. Wanneer de juiste gewichten worden gebruikt, kan dit het probleem van heteroscedasticiteit elimineren.
Gerelateerd :Hoe gewogen regressie uit te voeren in R
Aanname 4: Multivariate normaliteit
Bij meervoudige lineaire regressie wordt ervan uitgegaan dat de modelresiduen normaal verdeeld zijn.
Hoe te bepalen of aan deze veronderstelling wordt voldaan
Er zijn twee gebruikelijke manieren om te controleren of aan deze veronderstelling is voldaan:
1. Verifieer de hypothese visueel met behulp vanQQ-plots .
Een QQ-plot, een afkorting van quantile-quantile plot, is een type plot dat we kunnen gebruiken om te bepalen of de residuen van een model al dan niet een normale verdeling volgen. Als de punten op de grafiek grofweg een rechte diagonale lijn vormen, wordt aan de aanname van normaliteit voldaan.
De volgende QQ-plot toont een voorbeeld van residuen die grofweg een normale verdeling volgen:
De onderstaande QQ-grafiek toont echter een voorbeeld van een geval waarin de residuen duidelijk afwijken van een rechte diagonale lijn, wat aangeeft dat ze niet de normale verdeling volgen:
2. Verifieer de hypothese met behulp van een formele statistische test zoals Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre of D’Agostino-Pearson.
Houd er rekening mee dat deze tests gevoelig zijn voor grote steekproeven. Dat wil zeggen dat ze vaak concluderen dat residuen niet normaal zijn als uw steekproefomvang extreem groot is. Dit is de reden waarom het vaak gemakkelijker is om grafische methoden zoals een QQ-plot te gebruiken om deze hypothese te verifiëren.
Wat te doen als deze veronderstelling niet wordt gerespecteerd
Als niet aan de normaliteitsaanname wordt voldaan, heeft u verschillende opties:
1. Controleer eerst of er geen extreme uitschieters in de gegevens aanwezig zijn die resulteren in een schending van de normaliteitsaanname.
2. Vervolgens kun je een niet-lineaire transformatie op de responsvariabele toepassen, bijvoorbeeld door de vierkantswortel, log of derdemachtswortel te nemen van alle waarden van de responsvariabele. Dit resulteert vaak in een meer normale verdeling van modelresiduen.
Aanvullende bronnen
De volgende tutorials bieden aanvullende informatie over meervoudige lineaire regressie en de aannames ervan:
Inleiding tot meervoudige lineaire regressie
Een gids voor heteroskedasticiteit in regressieanalyse
Een gids voor multicollineariteit en VIF in regressie
De volgende tutorials bieden stapsgewijze voorbeelden van het uitvoeren van meervoudige lineaire regressie met behulp van verschillende statistische software:
Hoe u meerdere lineaire regressies uitvoert in Excel
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe u meervoudige lineaire regressie uitvoert in SPSS
Hoe meervoudige lineaire regressie uit te voeren in Stata
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder