R meervoudig of r vierkant: wat is het verschil?

Wanneer je met de meeste statistische software een regressiemodel fit, zul je in het resultaat vaak de volgende twee waarden tegenkomen:

Multiple R: de meervoudige correlatiecoëfficiënt tussen drie of meer variabelen.

R-kwadraat: Dit wordt berekend als (Multiple R) ² en vertegenwoordigt het deel van de variantie in deresponsvariabele van een regressiemodel dat kan worden verklaard door de voorspellende variabelen. Deze waarde varieert van 0 tot 1.

In de praktijk zijn we vaak geïnteresseerd in de R-kwadraatwaarde, omdat deze ons vertelt hoe nuttig de voorspellende variabelen zijn bij het voorspellen van de waarde van de responsvariabele.

Elke keer dat we echter een nieuwe voorspellende variabele aan het model toevoegen, wordt de R-kwadraat gegarandeerd groter, zelfs als de voorspellende variabele niet bruikbaar is.

Aangepaste R-kwadraat is een aangepaste versie van R-kwadraat die zich aanpast aan het aantal voorspellers in een regressiemodel. Het wordt als volgt berekend:

Aangepaste R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

Goud:

• R ² : De R ² van het model
• n : Het aantal waarnemingen
• k : het aantal voorspellende variabelen

Omdat R-kwadraat altijd toeneemt naarmate u meer voorspellers aan een model toevoegt, kan aangepaste R-kwadraat dienen als een metriek die u vertelt hoe nuttig een model is, aangepast op basis van het aantal voorspellers in een model .

Bekijk het volgende voorbeeld om elk van deze termen beter te begrijpen.

Voorbeeld: Meerdere R, R-kwadraat en aangepast R-kwadraat

Stel dat we de volgende dataset hebben die de volgende drie variabelen bevat voor 12 verschillende studenten:

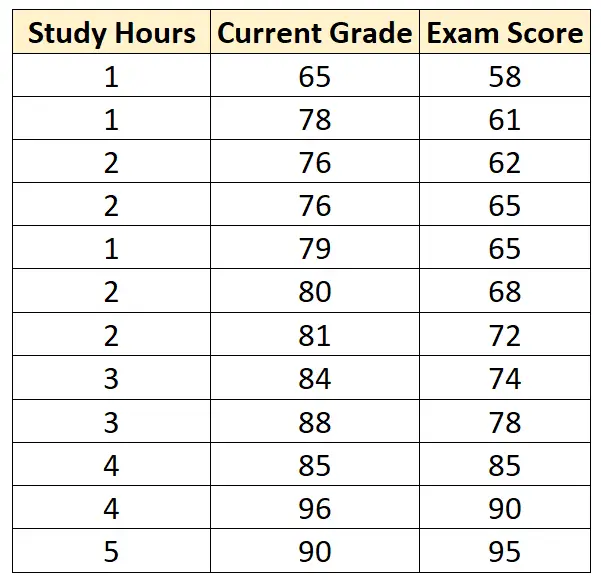
Stel dat we een meervoudig lineair regressiemodel passen met studie-uren en huidig cijfer als voorspellende variabelen en examenscore als responsvariabele, en verkrijgen het volgende resultaat:

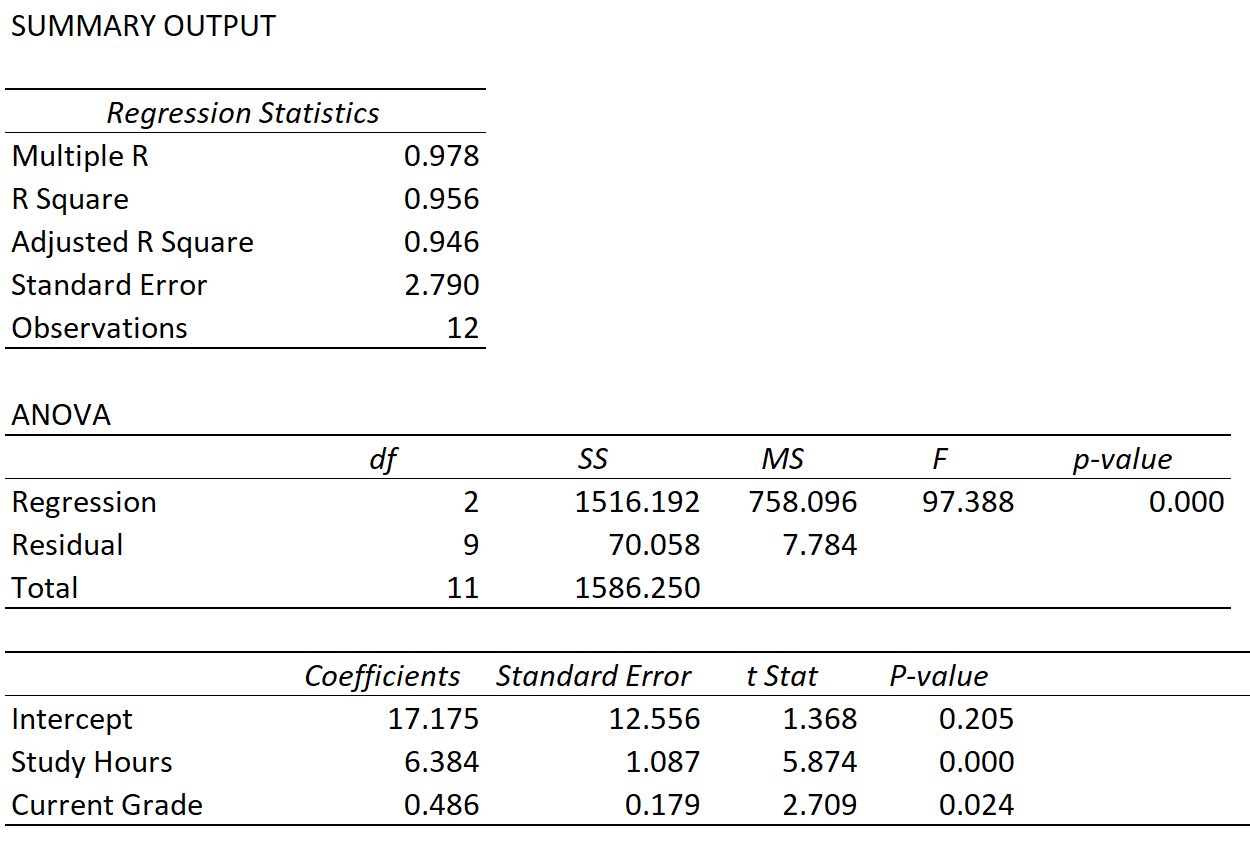
We kunnen de waarden van de volgende drie statistieken observeren:

Meerdere R: 0,978 . Dit vertegenwoordigt de meervoudige correlatie tussen de responsvariabele en de twee voorspellende variabelen.

R-kwadraat: 0,956 . Dit wordt berekend als (Meerdere R) ² = (0,978) ² = 0,956. Dit vertelt ons dat 95,6% van de variatie in examenscores kan worden verklaard door het aantal uren dat de studenten aan hun studie hebben besteed en hun huidige cijfer voor de cursus.

Aangepast R-kwadraat: 0,946 . Dit wordt als volgt berekend:

Aangepast R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0,946.

Dit vertegenwoordigt de R-kwadraatwaarde, aangepast voor het aantal voorspellende variabelen in het model .

Deze maatstaf zou nuttig zijn als we bijvoorbeeld een ander regressiemodel met 10 voorspellers zouden passen en zouden ontdekken dat de aangepaste R-kwadraat van dat model 0,88 was. Dit zou erop wijzen dat het regressiemodel met slechts twee voorspellers beter is omdat het een hogere aangepaste R-kwadraatwaarde heeft.

Aanvullende bronnen

Inleiding tot meervoudige lineaire regressie
Wat is een goede R-kwadraatwaarde?