Hoe u meerdere lineaire regressie uitvoert in sas

Meervoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen twee of meer voorspellende variabelen en eenresponsvariabele te begrijpen.

In deze zelfstudie wordt uitgelegd hoe u meerdere lineaire regressie uitvoert in SAS.

Stap 1: Creëer de gegevens

Stel dat we een meervoudig lineair regressiemodel willen toepassen dat het aantal uren dat aan studeren wordt besteed en het aantal afgelegde oefenexamens gebruikt om het eindexamencijfer van studenten te voorspellen:

Examenscore = β ₀ + β ₁ (uren) + β ₂ (voorbereidende examens)

Eerst gebruiken we de volgende code om een dataset te maken met deze informatie voor 20 studenten:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Stap 2: Voer meerdere lineaire regressie uit

Vervolgens zullen we proc reg gebruiken om een meervoudig lineair regressiemodel aan de gegevens te koppelen:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

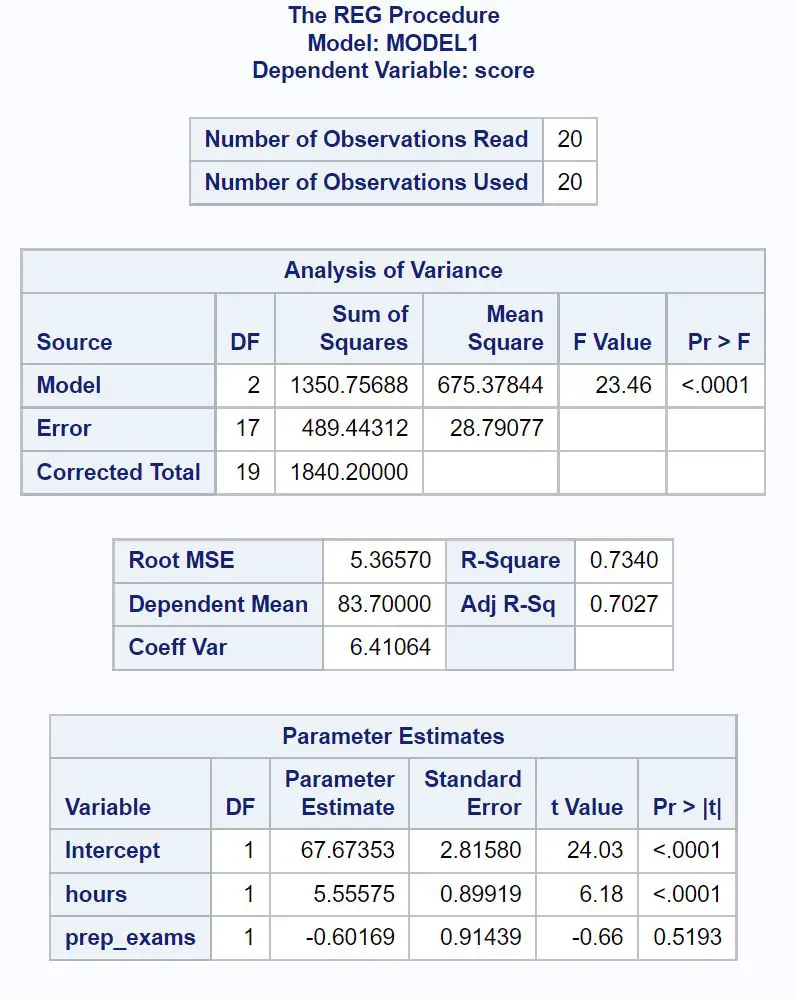
Zo interpreteert u de meest relevante cijfers in elke tabel:

Tabel met gap-analyse:

De totale F-waarde van het regressiemodel is 23,46 en de overeenkomstige p-waarde is <0,0001 .

Omdat deze p-waarde kleiner is dan 0,05 concluderen we dat het regressiemodel als geheel statistisch significant is.

Model passende tafel:

De R-Square- waarde vertelt ons het percentage variatie in examenscores dat kan worden verklaard door het aantal gestudeerde uren en het aantal afgelegde voorbereidende examens.

Over het algemeen geldt dat hoe groter de R-kwadraatwaarde van een regressiemodel is, hoe beter de voorspellende variabelen de waarde van de responsvariabele kunnen voorspellen.

In dit geval kan 73,4% van de variatie in examenscores worden verklaard door het aantal gestudeerde uren en het aantal afgelegde voorbereidende examens.

Ook de Root MSE- waarde is handig om te weten. Dit vertegenwoordigt de gemiddelde afstand tussen de waargenomen waarden en de regressielijn.

In dit regressiemodel wijken de waargenomen waarden gemiddeld 5,3657 eenheden af van de regressielijn.

Tabel met parameterschattingen:

We kunnen de parameterschattingswaarden in deze tabel gebruiken om de passende regressievergelijking te schrijven:

Examenscore = 67,674 + 5,556*(uren) – 0,602*(voorbereidingsexamens)

We kunnen deze vergelijking gebruiken om de geschatte examenscore van een student te vinden, op basis van het aantal uren studie en het aantal oefenexamens dat hij of zij heeft afgelegd.

Een student die bijvoorbeeld 3 uur studeert en 2 voorbereidende examens aflegt, zou een examenscore van 83,1 moeten krijgen:

Geschatte examenscore = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

De p-waarde voor uren (<0,0001) is kleiner dan 0,05, wat betekent dat er een statistisch significant verband bestaat met het examenresultaat.

De p-waarde voor voorbereidende examens (0,5193) is echter niet kleiner dan 0,05, wat betekent dat deze geen statistisch significant verband heeft met het examenresultaat.

We kunnen besluiten om voorbereidende examens uit het model te verwijderen, omdat deze niet statistisch significant zijn, en in plaats daarvan een eenvoudige lineaire regressie uit te voeren met bestudeerde uren als de enige voorspellende variabele.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe de correlatie in SAS te berekenen
Hoe u eenvoudige lineaire regressie uitvoert in SAS
Eenrichtings-ANOVA uitvoeren in SAS