Maatregelen van centrale tendens: definitie en voorbeelden
Een maatstaf voor de centrale tendens is een enkele waarde die het centrale punt van een dataset vertegenwoordigt. Deze waarde kan ook wel de ‘centrale locatie’ van een dataset worden genoemd.
In de statistieken zijn er drie veelgebruikte maatstaven voor de centrale tendens:
- Het gemiddelde
- De mediaan
- De mode
Elk van deze maatregelen vindt de centrale locatie van een dataset met behulp van verschillende methoden. Afhankelijk van het type gegevens dat u analyseert, is het wellicht beter om een van deze drie statistieken te gebruiken in plaats van de andere twee.
In dit artikel bekijken we hoe u elk van de drie maatstaven van de centrale tendens kunt berekenen en hoe u op basis van uw gegevens kunt bepalen welke maatstaf u het beste kunt gebruiken.
Waarom zijn metingen van de centrale tendens nuttig?
Voordat we kijken hoe we het gemiddelde, de mediaan en de modus kunnen berekenen, is het handig om te begrijpen waarom deze metingen überhaupt nuttig zijn.
Overweeg het volgende scenario:
Een jong stel probeert te beslissen waar ze hun eerste huis in een nieuwe stad willen kopen en het maximale dat ze kunnen uitgeven is $ 150.000. Sommige delen van de stad hebben dure huizen, andere goedkope huizen en weer andere huizen in het middensegment. Ze willen hun zoekopdracht eenvoudig verfijnen tot specifieke buurten die binnen hun budget passen.
Als het echtpaar alleen maar naar de prijzen van eengezinswoningen in elke buurt zou kijken, zouden ze moeite kunnen hebben om te bepalen welke buurten het beste bij hun budget passen, omdat ze zoiets als dit zouden kunnen zien:
Huizenprijzen in buurt A : $ 140.000, $ 190.000, $ 265.000, $ 115.000, $ 270.000, $ 240.000, $ 250.000, $ 180.000, $ 160.000, $ 200.000, $ 240.000, $ 280.000, …
Huizenprijzen in buurt B : $ 140.000, $ 290.000, $ 155.000, $ 165.000, $ 280.000, $ 220.000, $ 155.000, $ 185.000, $ 160.000, $ 200.000, $ 190.000, $ 140.000, $ 145,00 0,…
Huizenprijzen in buurt C : $ 140.000, $ 130.000, $ 165.000, $ 115.000, $ 170.000, $ 100.000, $ 150.000, $ 180.000, $ 190.000, $ 120.000, $ 110.000, $ 130.000, $ 120,00 0,…
Als ze echter de gemiddelde prijs (bijvoorbeeld een maatstaf voor de centrale tendens) van huizen in elke buurt zouden kennen, zouden ze hun zoekopdracht veel sneller kunnen verfijnen omdat ze gemakkelijker zouden kunnen identificeren welke buurt huizenprijzen heeft die passen bij hun budget:
Gemiddelde prijs van een huis in buurt A: $ 220.000
Gemiddelde prijs van een huis in buurt B : $190.000
Gemiddelde prijs van een huis in buurt C : $140.000
Door de gemiddelde huizenprijs in elke buurt te kennen, kunnen ze snel zien dat buurt C waarschijnlijk de meeste woningen beschikbaar heeft binnen hun budget.
Dit is het voordeel van het gebruik van een maatstaf voor de centrale tendens: het helpt je de centrale waarde van een dataset te begrijpen, die de neiging heeft te beschrijven waar de datawaarden over het algemeen liggen. In dit specifieke voorbeeld helpt het het jonge stel de typische prijs van een huis in elke buurt te begrijpen.
Afhaalmaaltijden: Een maatstaf voor de centrale tendens is nuttig omdat deze ons één enkele waarde oplevert die het ‘centrum’ van een dataset beschrijft. Dit helpt ons een dataset veel sneller te begrijpen dan alleen maar naar alle individuele waarden in de dataset te kijken.
Gemeen
De meest gebruikte maatstaf voor de centrale tendens is het gemiddelde . Om het gemiddelde van een dataset te berekenen, telt u eenvoudigweg alle individuele waarden bij elkaar op en deelt u deze door het totale aantal waarden.
Gemiddelde = (som van alle waarden) / (totaal aantal waarden)
Stel dat we bijvoorbeeld de volgende gegevensset hebben die het aantal homeruns weergeeft dat door 10 honkbalspelers in hetzelfde team gedurende een seizoen is geslagen:
| Speler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #tien |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Het gemiddelde aantal homeruns per speler kan als volgt worden berekend:
Gemiddeld = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 circuits .
Mediaan
De mediaan is de middelste waarde van een dataset. Je kunt de mediaan vinden door alle individuele waarden in een dataset te ordenen van klein naar groot en de mediaanwaarde te vinden. Als er een oneven aantal waarden is, is de mediaan de middelste waarde. Als er een even aantal waarden is, is de mediaan het gemiddelde van de twee middelste waarden.
Om bijvoorbeeld het gemiddelde aantal homeruns te vinden dat is geslagen door de 10 honkbalspelers in het vorige voorbeeld, kunnen we de spelers rangschikken in aflopende volgorde van het aantal geslagen homeruns:
| Speler | #1 | #6 | #7 | #5 | #tien | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Omdat we een even aantal waarden hebben, is de mediaan eenvoudigweg het gemiddelde van de twee middelste waarden: 13,5 .
Overweeg in plaats daarvan of we negen spelers hadden:
| Speler | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
Omdat we in dit geval een oneven aantal waarden hebben, is de mediaan eenvoudigweg de middelste waarde: 14 .
De mode
De modus is de waarde die het vaakst voorkomt in een dataset. Een dataset kan geen modi hebben (als er geen waarden worden herhaald), één modus of meerdere modi.
De volgende gegevensset heeft bijvoorbeeld geen modus:
| Speler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #tien |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
De volgende dataset heeft een modus: 15 . Dit is de waarde die het vaakst voorkomt.
| Speler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #tien |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
De volgende dataset heeft drie modi: 8, 15, 19 . Dit zijn de waarden die het vaakst voorkomen.
| Speler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #tien |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
De modus kan een bijzonder nuttige maatstaf zijn voor de centrale tendens bij het werken met categorische gegevens, omdat deze ons vertelt welke categorie het vaakst voorkomt. Beschouw bijvoorbeeld het volgende staafdiagram dat de resultaten toont van een enquête over de favoriete kleur van mensen:
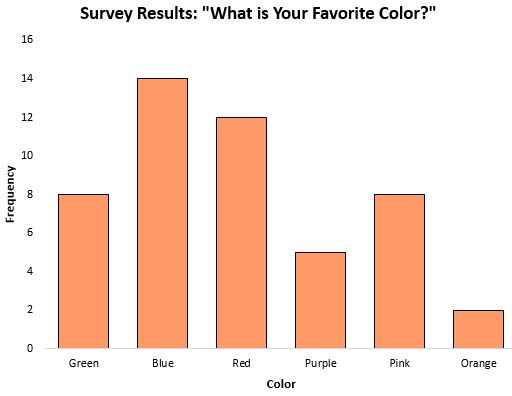
De modus , of de reactie die het vaakst voorkwam, was blauw.
In scenario’s waarin de gegevens categorisch zijn (zoals hierboven), is het niet eens mogelijk om de mediaan of het gemiddelde te berekenen, dus de modus is de enige maatstaf voor de centrale tendens die we kunnen gebruiken.
De modus kan ook worden gebruikt voor numerieke gegevens, zoals we in het bovenstaande voorbeeld zagen bij honkbalspelers. De modus is echter meestal minder nuttig voor het beantwoorden van de vraag „Wat is een typische waarde voor deze dataset?“ »
Stel dat we bijvoorbeeld het typische aantal homeruns willen weten dat een honkbalspeler in dit team slaat:
| Speler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #tien |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
De modus voor deze gegevensset is 8, 15 en 19 omdat dit de meest voorkomende waarden zijn. Deze zijn echter niet erg behulpzaam bij het begrijpen van het typische aantal homeruns dat een speler in het team slaat. Een betere maatstaf voor de centrale tendens zou in dit geval de mediaan (15) of het gemiddelde (ook 15) zijn.
De modus is ook een slechte maatstaf voor de centrale tendens als het een getal is dat ver verwijderd is van de rest van de waarden. De modus van de volgende dataset is bijvoorbeeld 30, maar dit vertegenwoordigt niet echt het „typische“ aantal homeruns per speler in het team:
| Speler | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #tien |
|---|---|---|---|---|---|---|---|---|---|---|
| Thuisloop | 5 | 6 | 7 | tien | 11 | 12 | 13 | 15 | 30 | 30 |
Nogmaals, het gemiddelde of de mediaan zou de centrale locatie van deze dataset beter kunnen beschrijven.
Wanneer moet u gemiddelde, mediaan en modus gebruiken?
We hebben gezien dat het gemiddelde, de mediaan en de modus allemaal op heel verschillende manieren de centrale locatie, of ‘typische waarde’, van een dataset meten:
Gemiddelde: Vindt de gemiddelde waarde in een dataset.
Mediaan: Vindt de mediaanwaarde in een gegevensset.
Modus: Vindt de meest voorkomende waarde in een dataset.
Hier zijn scenario’s waarin bepaalde maatstaven van centrale tendens beter te gebruiken zijn dan andere:
Wanneer moet u het gemiddelde gebruiken?
Het is het beste om het gemiddelde te gebruiken als de gegevensverdeling redelijk symmetrisch is en er geen uitschieters zijn.
Stel dat we bijvoorbeeld de volgende verdeling hebben die de salarissen van individuen in een bepaalde stad weergeeft:

Omdat deze verdeling redelijk symmetrisch is (dwz als je hem in tweeën deelt, ziet elke helft er ongeveer gelijk uit) en er geen uitschieters zijn (dat wil zeggen (zeg geen extreem hoge salarissen), zal het gemiddelde deze dataset goed kunnen beschrijven.
Het gemiddelde blijkt $63.000 te zijn, wat ongeveer in het midden van de verdeling ligt:

Wanneer moet u de mediaan gebruiken?
Het is het beste om de mediaan te gebruiken als de gegevensverdeling scheef is of als er uitschieters zijn.
Bevooroordeelde gegevens:
Wanneer de verdeling scheef is, slaagt de mediaan er nog steeds in de centrale locatie vast te leggen. Beschouw bijvoorbeeld de volgende verdeling van de salarissen van individuen in een bepaalde stad:

De mediaan weerspiegelt beter het “typische” salaris van een individu dan het gemiddelde. Dit komt omdat grote waarden aan de staart van een verdeling de neiging hebben om het gemiddelde van het midden naar de lange staart te verplaatsen.
In dit specifieke voorbeeld vertelt het gemiddelde ons dat een gemiddeld individu ongeveer $47.000 per jaar verdient in deze stad, terwijl de mediaan ons vertelt dat het typische individu slechts ongeveer $32.000 per jaar verdient, wat veel representatiever is voor het typische individu.
Uitschieters:
De mediaan helpt ook om de centrale locatie van een verdeling beter vast te leggen als er uitschieters in de gegevens voorkomen. Bekijk bijvoorbeeld de volgende grafiek die de vierkante meters van huizen in een bepaalde straat laat zien:

Het gemiddelde wordt sterk beïnvloed door enkele extreem grote huizen, terwijl de mediaan dat niet is. De mediaan kan dus beter de ‘typische’ vierkante meters van een huis in die straat vastleggen dan het gemiddelde.
Wanneer moet u de modus gebruiken?
Deze modus kunt u het beste gebruiken als u met categorische gegevens werkt en wilt weten welke categorie het vaakst voorkomt. Hier zijn enkele voorbeelden:
- U voert een onderzoek uit naar de favoriete kleuren van mensen en wilt weten welke kleur het vaakst voorkomt in de reacties.
- U doet een onderzoek naar de voorkeuren van mensen uit drie keuzes voor website-ontwerp en wilt weten welk ontwerp mensen het liefst hebben.
Zoals eerder vermeld, is het, als je met categorische gegevens werkt, niet eens mogelijk om de mediaan of het gemiddelde te berekenen, waardoor de modus de enige maatstaf voor de centrale tendens blijft.
Als u met numerieke gegevens werkt, zoals het aantal vierkante meters huizen, het aantal homeruns per speler, het salaris per individu, etc., kunt u doorgaans het beste de mediaan of het gemiddelde gebruiken om de waarde ‘typisch’ te beschrijven. de dataset.
Opmerking: Het is belangrijk op te merken dat als een gegevensset perfect normaal verdeeld is, het gemiddelde, de mediaan en de modus allemaal dezelfde waarde hebben.